本記事では、RWKVとよばれるモデルのアーキテクチャについて詳しく説明します。
はじめに
自然言語処理の分野において、Transformer[1]の登場以前に一般的に使用されてきたRNN[2]はいくつかの課題を抱えており、その課題を克服する新たな手法として、RNNとは完全に異なるアプローチを取るTransformerが登場しました。しかし、Transformerにも解決すべき問題が存在しています。そこで、これらのアプローチを結びつけて進化させていく必要が出てきました。
まず、RNNの利点と欠点を見てみましょう。RNNは、文章の長さにほとんど制約がなく、計算コストも比較的小さいという利点があります。しかし、以前の入力を正確に記憶することが難しく(長期依存性を捉えられない)、学習を高速化することも難しい(学習並列化が困難)という欠点も存在します。
一方、Transformerは長期依存性を捉えることが可能で性能も高いという利点があります。また、学習を効率的に進めることができる(学習並列化が可能)という長所もあります。しかしながら、計算コストや必要なメモリサイズが系列長に応じて急激に増加するという問題もあり、RNNと同様に理論上は扱える系列長は無限ですが、実運用上はハードウェアの制約を強く受けることになり、RNNに比べて長い系列を扱いにくいという欠点があります。
こうしてみると、それぞれの手法の利点と欠点は正反対になっています。ですから、両者の利点を結合したモデル、つまり、RNNのように長い文章を扱うことができ、計算コストが小さく、Transformerのように長期の依存関係も捉えられ、さらに学習を並列化して高速化できるモデルの実現を目指す流れは必然と言えるでしょう。
このような理想的なモデルの実現に向けた第一歩が、今回紹介するRWKV(Receptance Weighted Key Value)[3]です。
本記事では、RWKVの仕組みについて分かりやすく解説していきます。
RWKV登場までの流れ
Transformerの登場
RWKVの登場までの経緯について、先ほどよりも詳しく説明します。
Transformerが登場する以前、深層学習は機械学習分野で大きな成功を収めていました。特に注目すべきは、画像処理で成果を上げたCNN[4]と、系列処理で成果を上げたRNNです。しかしながら、これらの手法にも課題が存在していました。
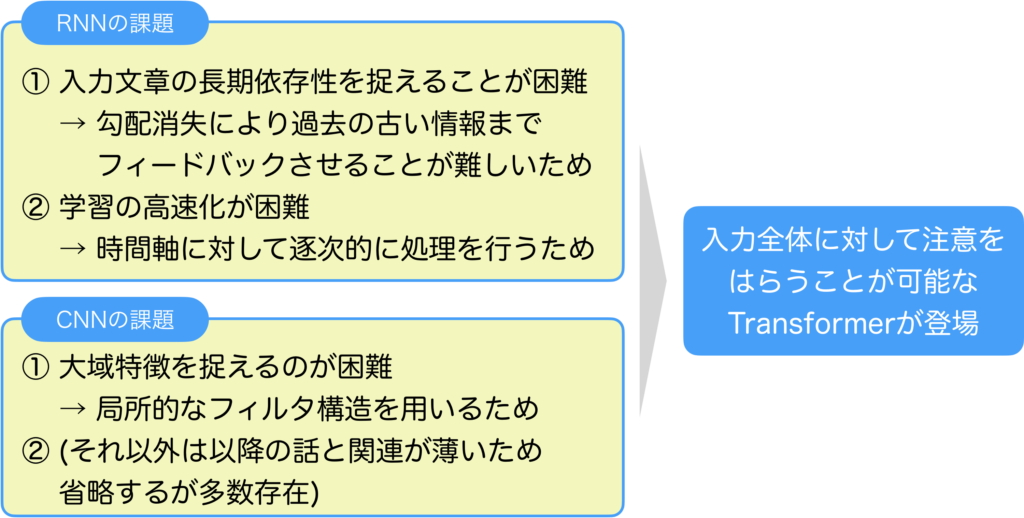
具体的に、RNNには長期依存性を捉えることが困難、そして学習の高速化が困難という2つの課題がありました。長期依存性を捉えるのが難しいのは、学習時に過去の情報をフィードバックする際に、途中で勾配が消失してしまい、長期的な特徴をうまく学習できないためです。また、学習の高速化が難しいのは、入力系列を時刻ごとに逐次的に処理する必要があるためです。RNNは内部に再帰構造を持つため、過去の情報を保持しながら処理を進める必要があります。逆に言えば、各時刻での計算コストは小さいという利点もあります。RNNの欠点を補う手段としてCNNを導入するというものがありますが、それにも限界がありました。CNNで系列処理を行う際には、1次元畳み込みフィルタを用いますが、畳み込みフィルタは考慮可能な時間的な領域に明確な線引きがあるため、長期的な特徴を捉えるには多層にする必要があります。ただし、考慮可能な領域を無限にするには層数も無限にする必要があり現実的な代替手段にはなりませんでした。
そこで、新しいモデルであるTransformerが生まれたのです。Transformerは、系列全体を一括して入力として受け取り、全トークン間の組み合わせを毎回計算することで長期依存性を捉えることが可能になりました。内部に再帰性を持たないため、並列処理も実現できるようになったのです。
Transformerの登場については以下の記事で詳しく説明していますので、興味がありましたら参考にしてください。
Transformerの万能性と課題
Transformerは元々自然言語処理のために登場しましたが、後に画像認識でも優れた結果を示しました。多くの研究者がTransformerのこのような万能性に注目していますが、なぜそんなに優れているのでしょうか。
答えは「帰納バイアス[5]の低さ」にあります。帰納バイアスとは、モデルの汎用性を説明する際の考え方の一つです。例えば、画像処理には空間フィルタを持つニューラルネットが、自然言語処理には再帰構造を持つニューラルネットが適しているとされています。これらは特定のタスクに特化した高性能なモデルで、帰納バイアスが高いです。高い帰納バイアスを持つモデルは、もともと想定されていない領域で高性能を実現することは難しいです。
それに対して、Transformerはもともと想定されていなかった画像処理や強化学習などの領域でも高い性能を実現しています。この適用範囲の広さは、汎用性の高いモデルアーキテクチャを持っていることを意味し、帰納バイアスが低いと言えます。
この、Transformerの帰納バイアスの低さが万能さの秘密です。
帰納バイアスについては以下の記事で詳しく説明しています。
Transformerの帰納バイアスの低さを活用して、入力モダリティの制約の少ないより汎用的なモデルとしてPerceiver[6]が提案されています。Perceiverについては以下の記事で詳しく説明していますので、興味がありましたら是非読んでみてください。
Transformerの成功の背後には、その独特な構造があります。Transformerは注意(attention)機構を核としていますが、その周囲にはLayerNormalizationやフィードフォワードネットワークといった要素が組み込まれ、ブロック構造(Transformer Block)を形成しています。このブロック構造の優れた設計が、モデルの帰納バイアスを低く保っているといえます。さらに興味深いことに、このブロック構造は非常に柔軟で、注意機構を他のネットワーク要素に置き換えても、高い性能を維持することが可能です。このような変種は「MetaFormer[7]」として知られています。
MetaFormerでは、注意機構をトークンミキサーとして考えています。トークン間の処理が可能であれば、注意機構は必須ではなく、単純なプーリングだけでも十分なのではないか、というのがMetaFormerの提案の背景にあります。ただし、このアイディアの検証は画像処理の分野にとどまっています。しかし、近年の研究の流れを見る限りは、自然言語処理の分野でも注意機構を置き換える研究は多く行われており、同様のことが自然言語処理の分野でもいえる可能性があります。ただし、注意機構の置き換えについては、多少は性能とのトレードオフを考慮しなければならない面があり、注意機構の万能さは揺るがないものと考えられます。
以上から、Transformerの万能さの要因は、次の2つが大きく関連していると考えられます。
①モデル構造の高い抽象性
②注意機構の高い汎用性
しかし、Transformerも完璧なモデルではありません。特に内積注意に関連する計算コストの高さや、大量のメモリ要件という課題が挙げられます。現代のコンピュータでは、これらの問題は避けられない制約となっており、量子コンピュータのような超高速計算と大容量メモリが利用できる環境を前提としない限り、計算コストを削減する方法を模索する必要があります。この課題を解決するための研究が現在も活発に進められています。
Attention Free Transformer
計算コストやメモリ要件といった課題があることを述べましたが、これらの課題は端的にいうと、長い文章を効率的に扱いたいという目的を達成しようとすると問題になるものです。長文の処理を可能にするための方法として、下図にも示されていますが、注意機構の改良や入力の改良が考えられます。注意機構を改良するアプローチとしては、計算コストが高い内積注意を効率的に近似計算する手法や、内積注意を他の手法に置き換える方法が存在します。また、入力の改良では、入力データを圧縮するか、分割して入力する方法があります。
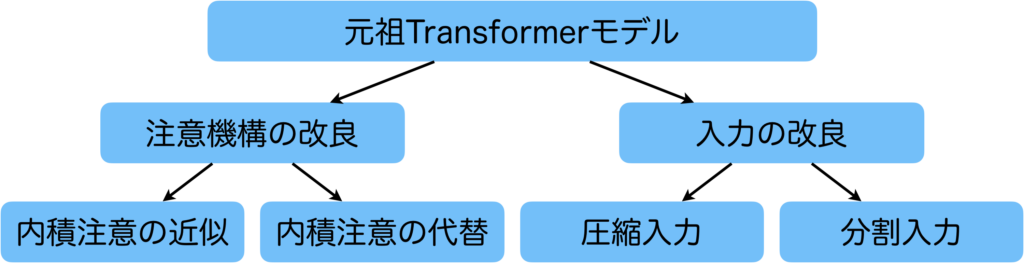
RWKVが特に関連するのは、内積注意を代替する方法であり、そのアプローチを採用したAttention Free Transformer[8]から大きな影響を受けています。
Attention Free Transformerとは、TransformerのMulti-Head Attentionを、ゲーティングとWKV(Weighted key Value)による機構で置き換えた手法です。内積注意を無くし、複数のヘッドを用いない手法にすることで圧倒的な計算コストの低減を実現しました。
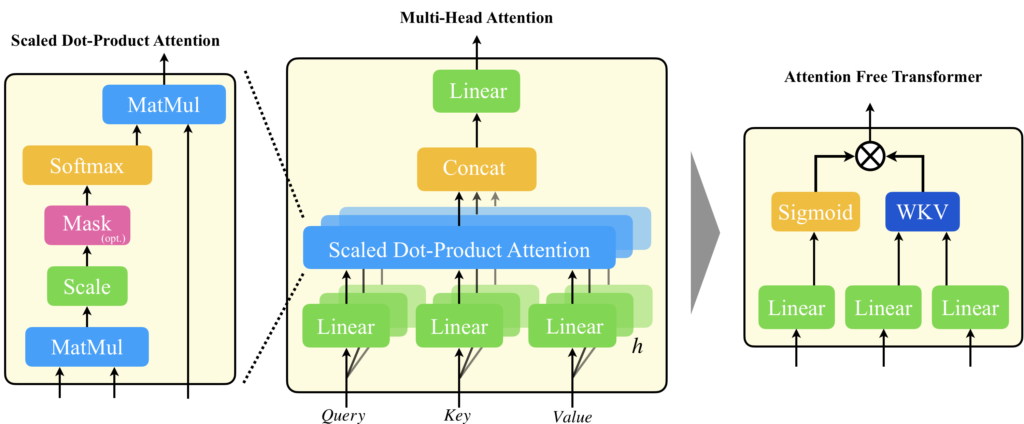
Attention Free Transformerの詳細の計算式などが気になる方は、以下の記事を参考にしていただければと思います。
RWKVの登場
内積注意は、QueryとKeyの間で全入力トークンに対する内積計算が不可欠だったため、新しいトークンが生成されるたびに、それを含む過去の全てのトークン列を入力する必要があり、それが計算コストがかさむ要因となっていました。Attention Free Transformerの登場により、QueryとKeyの内積計算を必要としない新しい注意機構、Weighted Key Value(WKV)方式が提案され、内積の計算が不要になり計算コストを大幅に改善することができました。しかし、Attention Free Transformerでは、まだ過去のすべての情報を入力する必要があったため、RWKVではそれを改良し、WKVに再帰的性質を取り入れることで、以前の全ての情報を入力することなく、効率的に処理を行えるReceptance Weighted Key Value方式を提案しました。
再帰性を導入することで、並列演算が困難になるという疑問が浮かぶかもしれません。確かに、再帰的な部分に関しては時間軸上でのシリアルな計算が必須です。しかしながら、この影響を最小限に抑えるテクニックがあります。具体的には、再帰的なループを持つ構造を、できるだけ小さな内部メカニズムに限定することです。この工夫により、再帰的な部分の前後での計算は並列的に高速に実行することができます。RWKVでは、再帰性をWKVだけに限定しているため、それ以外の部分は並列で高速に計算することができるので、学習フェーズでは並列計算のメリットを享受しつつ、推論時にはRNNのような効率的な計算が可能になっています。
RWKVのポイント
- RNNとTransformerの利点を組み合わせたモデル
- 学習時は処理を並列化して高速に実行可能
- 推論時は現在の入力と状態変数を用いて少ない計算コストで実行可能
- 上記を実現するためにRWKV Attentionを導入
RWKVのアーキテクチャ
RWKVの基本構造
まずは、RWKVの基本構造から確認してみましょう。下図左にTransformer Block、右にRWKV Blockを示しました。見てもらうと分かると思いますが、RWKVの基本構造はTransformerと同様になっています。違いは、Multi-Head AttentionがTime Mixingに、Feed ForwardがChannel Mixinfに替わっている点と、それぞれ再帰構造を持つ点です。
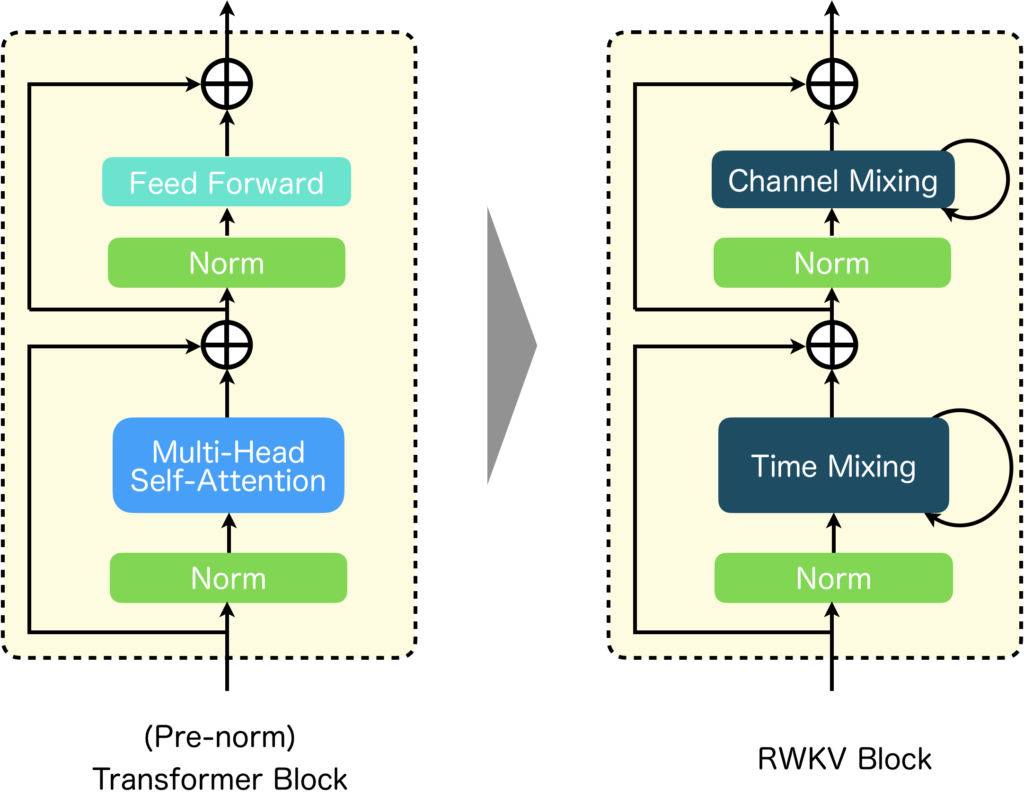
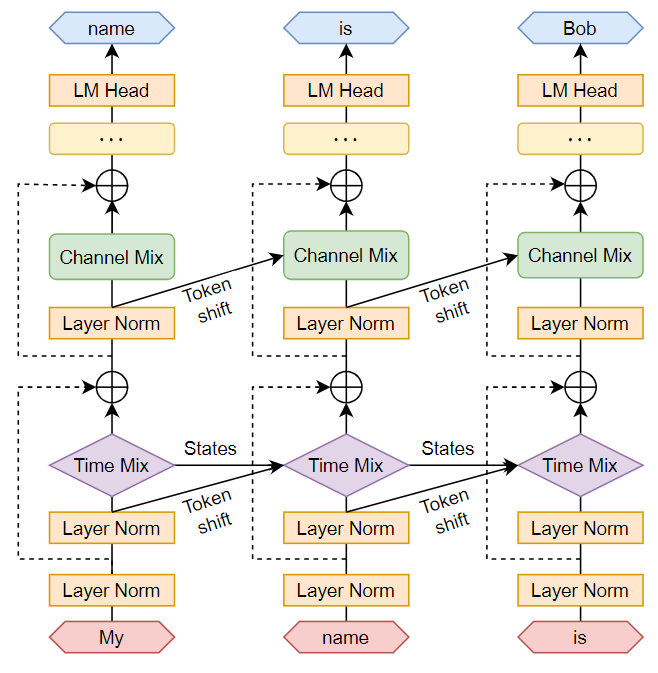
RWKVを用いて系列処理を行う際の情報の流れを、時間軸方向に展開した再帰構造で考えてみましょう。以下の図では、RWKVを使った文章生成の一例を示しています。
RWKVを使用すると、各ステップに必要な入力は1トークンだけです。したがって、「My」、「name」、「is」というように、一つずつ順に入力していけば良いのです。
※一方、Transformerを使用する場合、例えば「My」の後に「My name」、その後に「My name is」と、前の入力も含めて入力する必要がありました。
RWKVの再帰的な構造には、「Token shift」と「States」の二つの要素があります。「Token shift」とは、一つ前の入力トークンを保持し、次の時刻での処理に使用するための情報の流れを指します。「States」は、WKVの内部状態を示しています。
Time Mixing
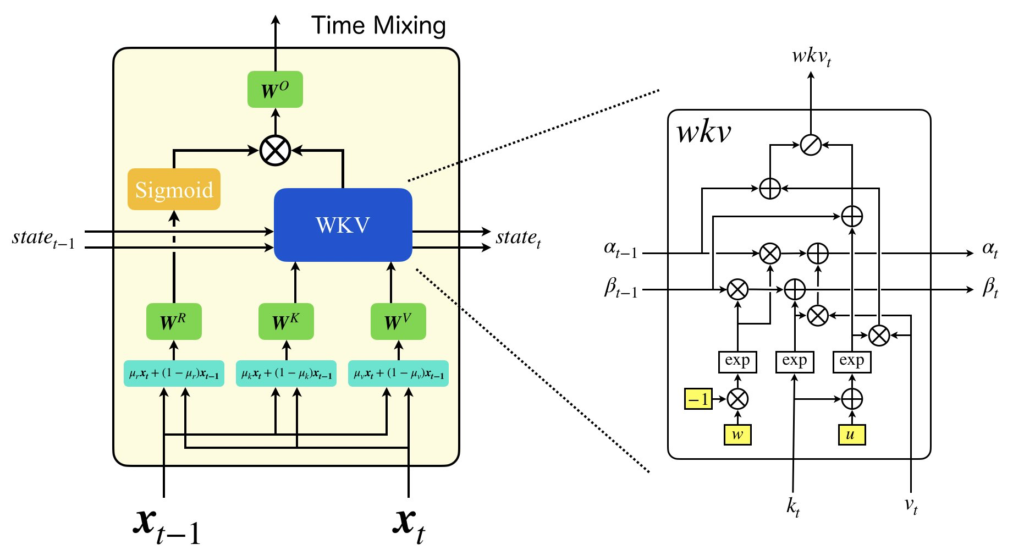
Time Mixingの機能について、詳しくご理解いただくため、まず数式の解説から始めていきます。以下がTime Mixingの数式です。
$$\begin{eqnarray}
\boldsymbol{r}_t &=& \boldsymbol{W_r}\cdot (\mu_r \boldsymbol{x}_t + (1-\mu_r)\boldsymbol{x}_{t-1}) \\
\boldsymbol{k}_t &=& \boldsymbol{W_k}\cdot (\mu_k \boldsymbol{x}_t + (1-\mu_k)\boldsymbol{x}_{t-1}) \\
\boldsymbol{v}_t &=& \boldsymbol{W_v}\cdot (\mu_v \boldsymbol{x}_t + (1-\mu_v)\boldsymbol{x}_{t-1}) \\
\boldsymbol{wkv}_t &=& \frac{\sum_{i=1}^{t-1}\exp(-(t-1-i)w + \boldsymbol{k}_i)\boldsymbol{v}_i + \exp(u + \boldsymbol{k}_t)\boldsymbol{v}_t}{\sum_{i=1}^{t-1}\exp(-(t-1-i)w + \boldsymbol{k}_i) + \exp(u + \boldsymbol{k}_t)}\\
\boldsymbol{o}_t &=& \boldsymbol{W_o}\cdot (\sigma (r_t)\odot \boldsymbol{wkv}_t)
\end{eqnarray}$$
Time Mixingは、RWKVのベースとなったAttention Free Transformer(以降、AFT)と同様に、Multi-Head Attentionを代替するため、線形層も組み込まれています。RWKVを構築するTime Mixingの入力は、AFTとは異なり、過去のトークンを含んでいますが、必要なのは現在の入力\(\boldsymbol{x}_t\)と直前の入力\(\boldsymbol{x}_{t-1}\)のみです。そして、これらは直接線形層で変換されるのではなく、パラメータ\(\mu\)を使って線形結合され、その後変換されます(\(\boldsymbol{r}_t, \boldsymbol{k}_t, \boldsymbol{v}_t\))。 ここまでの説明では、標準のAttentionとは少し異なる計算をしているのが分かりますが、大きな障壁なく理解できるかと思います。続いて、\(\boldsymbol{wkv}_t\)の計算詳細を見ていきましょう。この計算は少し複雑ですが、RWKVの中心的な部分です。さて、\(\boldsymbol{wkv}_t\)の計算式を見ると、過去の\(\boldsymbol{k}\)と\(\boldsymbol{v}\)を使用しているため、一見、再帰的な計算がないように感じるかもしれません。しかし、実際には、後に紹介する状態変数\(\boldsymbol{\alpha}\)と\(\boldsymbol{\beta}\)を用いて、RNNのように前の状態を用いて効率的に計算することができます。 \(\boldsymbol{\alpha}\)と\(\boldsymbol{\beta}\)の定義は次のようになります。
$$\begin{eqnarray}
\boldsymbol{\alpha}_t &=& \sum_{i=1}^{t}\exp(-(t-i)w + \boldsymbol{k}_i)\boldsymbol{v}_i \\
\boldsymbol{\beta}_t &=& \sum_{i=1}^{t}\exp(-(t-i)w + \boldsymbol{k}_i
\end{eqnarray}$$
これにより、以下の漸化式でそれぞれの変数を表すことができます。
$$\begin{eqnarray}
\boldsymbol{\alpha}_t &=& \exp(-w)\boldsymbol{\alpha}_{t-1} + \exp(\boldsymbol{k}_t)\boldsymbol{v}_t\\
\boldsymbol{\beta}_t &=& \exp(-w)\boldsymbol{\beta}_{t-1} + \exp(\boldsymbol{k}_t)
\end{eqnarray}$$
このとき、\(\boldsymbol{wkv}\)は状態変数を用いて以下のよう計算されます。
$$
\boldsymbol{wkv}_t = \frac{\boldsymbol{\alpha}_{t-1} + \exp(u + \boldsymbol{k}_t)\boldsymbol{v}_t}{\boldsymbol{\beta}_{t-1} + \exp(u + \boldsymbol{k}_t)}
$$
状態変数\(\boldsymbol{\alpha}\)と\(\boldsymbol{\beta}\)を用いることで、過去の情報を再計算することなく効率的に計算できます。この特徴が、RNNのような高速な推論や、長いテキストのシーケンスを扱うことを可能にしています。 これらの数式を通して、RWKVのTime Mixingの核心を理解していただけたかと思います。さらに深い理解のため、数式を図で表現してみました。図を参考に、もう一度数式を確認してみてください。
Channel Mixing
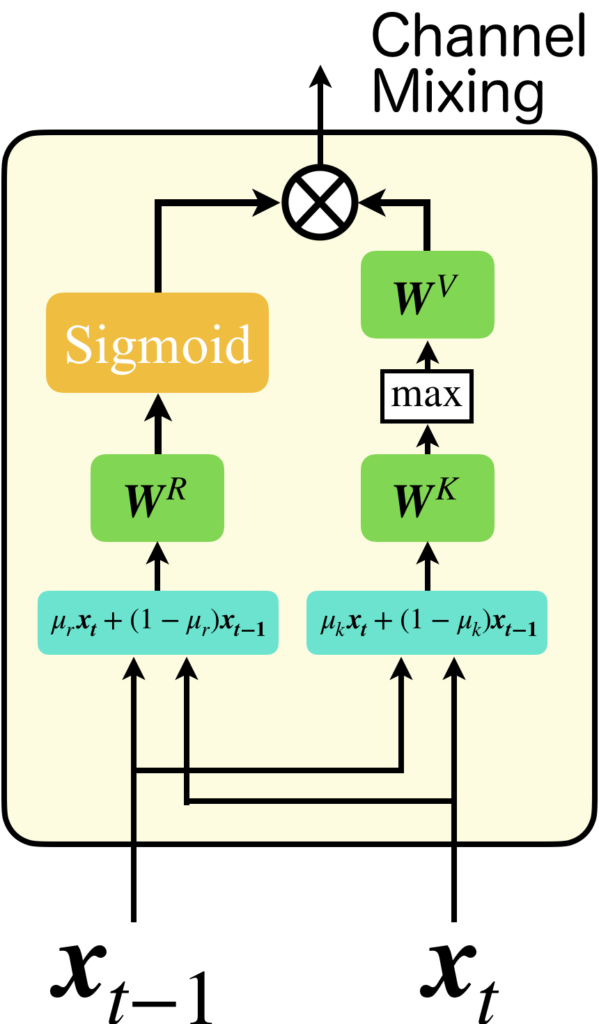
RWKVのもう一つの重要な仕組みである、Channel Mixingについて説明します。
Channel Mixingは以下の数式で表されます。
$$\begin{eqnarray}
r_t &=& \boldsymbol{W_r}\cdot (\mu_r x_t + (1-\mu_r)x_{t-1}) \\
k_t &=& \boldsymbol{W_k}\cdot (\mu_k x_t + (1-\mu_k)x_{t-1}) \\
o_t &=& \sigma (r_t) \odot (\boldsymbol{W_v} \cdot \max (k_t, 0)^2)
\end{eqnarray}$$
この数式はTime Mixingよりも非常にシンプルな形になっています。入力としては時刻\(t\)と時刻\(t-1\)の2つを用い、それらをパラメータ\(\mu\)により線形結合して処理します。数式には、\(\boldsymbol{W_r}, \boldsymbol{W_k}, \boldsymbol{W_v}\)の3つの重み行列が含まれていますが、これらはTime Mixingの重みとは共有されていません。図解すると、右側の\(\boldsymbol{W_k}\)や\( \boldsymbol{W_v}\)のあるパスは、中間層の活性化関数が\(\max(\boldsymbol{k}, 0)^2\)、出力層の活性化関数が恒等関数の3層ニューラルネットワークと考えることができます。その結果を左側の列、つまり2層ニューラルネットワークでゲーティングする形になっています。
推論時に高速化が可能な理由
RWKVがRNNの特性を持つことで、推論の際に非常に高速に処理することが可能となっています。
具体的に、通常のTransformerを使って「My name is Bob」という文章を処理する場面を考えてみましょう。この場合、
時刻1: <入力>My<出力>name
時刻2: <入力>My name<出力>is
時刻3: <入力>My name is<出力>Bob
というように、各時刻での単語ベクトルを生成し、それを含む過去全てのトークンを再度入力として次の単語を予測するための処理を繰り返す必要があります。
しかし、RWKVの場合は過去の状態を保持しているので、次のようなシンプルな処理が可能です。
時刻1: <入力>My<出力>name
時刻2: <入力>name<出力>is
時刻3: <入力>is<出力>Bob
この方式は、RNNのメリットをTransformerに取り入れたもので、処理の効率を大きく向上させています。その結果、例えばRaspberry Piのようなデバイスでも、RWKVを動かすことができます。
学習時に並列化が可能な理由
推論時に計算コストが大幅に削減されることを説明しましたが、「では学習時はどうなのか?」という疑問が浮かびますよね。実は、学習時はRWKVは並列処理が可能であり、これはTransformerの大きな利点である並列計算能力を継承しているのです。
具体的な方法を説明するため、「My name is Bob」という入力テキストを例にとって考えてみましょう。
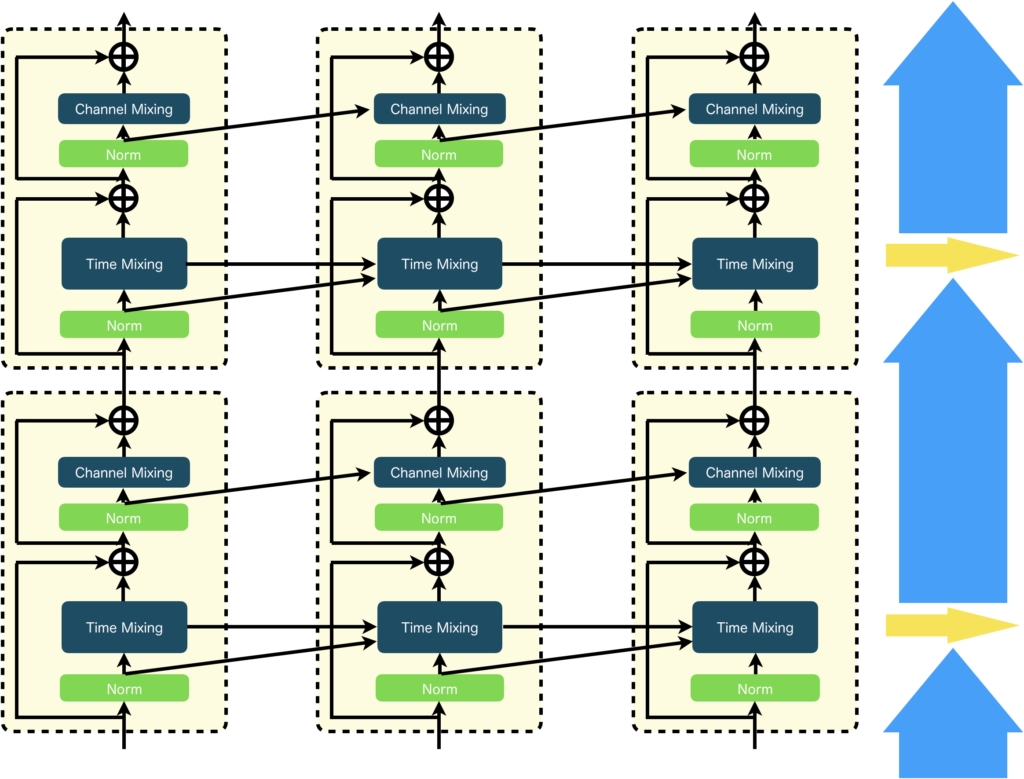
推論時とは違い、学習時には前の時刻の処理を最後まで待つことなく、「My name is」という入力から「name is Bob」という出力を生成することができます。具体的には、「My name is」についてTime Mixingの直前までバッチ処理してしまいます(下図において青色矢印)。Time Mixingについては、状態を持ちますからシリアルに計算する必要があります(下図において黄色矢印)。とはいえ、それはTime Mixingの部分だけで済むわけです。それ以外の部分は一気にバッチ処理してしまいます(下図において青色矢印)。 要するに、状態ベクトルである\(\boldsymbol{\alpha}\)と\(\boldsymbol{\beta}\)を除いては、学習データをバッチ化して並列に計算することが可能なのです。
まとめ
RWKVは、評価指標上では他のTransformerベースの手法と並ぶ性能を持つとされています。しかし、内積注意と異なり、過去の情報を特定して振り返る能力に制約があるため、過去の明確な情報へのアクセスが必要なシチュエーションでは、Transformerに比べて性能が低下する可能性が指摘されています。この点は、論文でも確認されており、今後の研究の課題として挙げられています。
このため、複雑なタスク、例えば入試問題を解くようなシチュエーションではRWKVの性能に期待が持てないかもしれません。一方で、組み込み機器にRWKVを導入して会話ロボットを作るなど、簡単な日常会話程度の利用であれば、利用できるかもしれません。
ですが、現状だとRWKVは、あまり高い性能とは言えない印象を受けます。性能面でいうと、多少の遅延やトークン数に制約があっても内積注意ベースのTransformerの方が魅力的に感じます。
しかし、RWKVには大きなポテンシャルがあると感じています。ですので、今後の動向に注目したいと思います。
参考文献
[1] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin, "Attention is all you need," in Proc. NeurIPS, 2017.
[2] David E. Rumelhart and James L. McClelland, “Learning Internal Representations by Error Propagation,” in Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations, 1987.
[3] Bo Peng, Eric Alcaide, Quentin Anthony, Alon Albalak, Samuel Arcadinho, Huanqi Cao, Xin Cheng, Michael Chung, Matteo Grella, Kranthi Kiran GV, Xuzheng He, Haowen Hou, Przemyslaw Kazienko, Jan Kocon, Jiaming Kong, Bartlomiej Koptyra, Hayden Lau, Krishna Sri Ipsit Mantri, Ferdinand Mom, Atsushi Saito, Xiangru Tang, Bolun Wang, Johan S. Wind, Stansilaw Wozniak, Ruichong Zhang, Zhenyuan Zhang, Qihang Zhao, Peng Zhou, Jian Zhu, and Rui-Jie Zhu, "RWKV: Reinventing RNNs for the Transformer Era," arXiv, 2023.
[4] Kunihiko Fukushima, "Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position," Biological Cybernetics, 1980.
[5] Tom Michael Mitchell, "The Need for Biases in Learning Generalizations," 2007.
[6] Andrew Jaegle, Felix Gimeno, Andrew Brock, Andrew Zisserman, Oriol Vinyals and Joao Carreira. "Perceiver: General Perception with Iterative Attention," in Proc. ICML, 2021.
[7] Weihao Yu, Mi Luo, Pan Zhou, Chenyang Si, Yichen Zhou, Xinchao Wang, Jiashi Feng, and Shuicheng Yan. "MetaFormer is Actually What You Need for Vision," in Proc. CVPR, 2021.
[8] Shuangfei Zhai, Walter Talbott, Nitish Srivastava, Chen Huang, Hanlin Goh, Ruixiang Zhang, and Josh Susskind, "An Attention Free Transformer," arXiv, 2021.