【図解】運動学入門：順運動学と逆運動学について解説！

この記事では、運動学について、初心者でもわかるように解説していきます。

ぜひ最後までお読み頂けると幸いです。

※内容に誤りがないよう心がけていますが、もし間違いを見つけられたときは、「お問い合わせフォーム」からお伝えいただけると大変助かります。

また、本記事の内容をベースとした、4脚ロボットの順運動学と逆運動学を導出する記事も執筆しましたので、併せてお読みいただけると幸いです。

【図解】4脚ロボットの順運動学と逆運動学

本記事では、4脚ロボットの運動学（順運動学と逆運動学）に焦点をあてて、一般的な4脚ロボットの歩行制御で利用可能な一般化された運動学の式を導出することを目標に解説していきます。 運動学（順運動学と逆運動 ...

この記事の内容は動画でも解説しています。動画もぜひご活用ください。

運動学

ここでは、運動学について、その概要と、運動学の種類、導出方法などについて解説します。

運動学とは

運動学（Kinematics）とは、ロボットの関節角度とエンドエフェクタ（先端）の位置や姿勢の関係を数式で表現することを扱う学問です。

ここで、エンドエフェクタの位置と姿勢の違いについて補足します。エンドエフェクタの位置とは、どこにあるかを表す座標情報になります。エンドエフェクタの姿勢とは、エンドエフェクタがどのような向き、回転となっているかを表します。具体例をみてみましょう。以下の図のように、アームロボットがリンゴを取りに行くことを考えます。エンドエフェクタの目標位置はりんごの位置となり、一意に決まります。しかし、上から取るのか横から取るのかによってエンドエフェクタの向きや回転、すなわち姿勢が変化します。これが、エンドエフェクタの位置と姿勢の違いです。

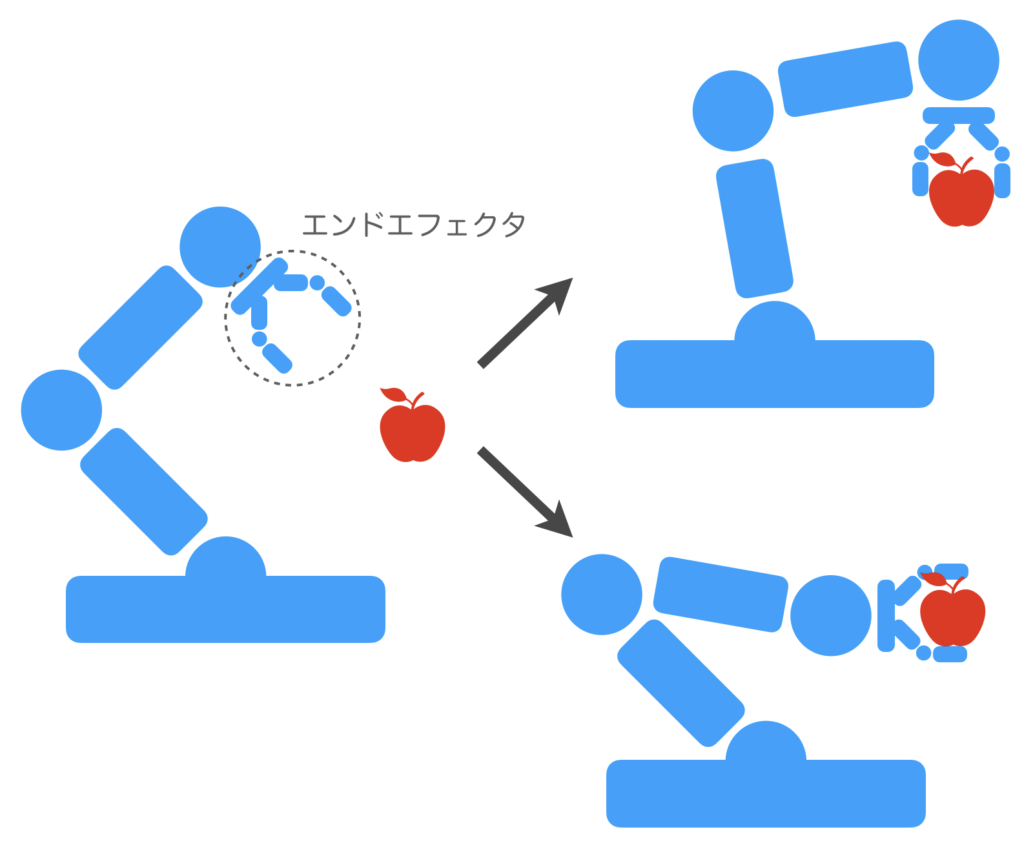
少々補足が長くなりましたが、運動学が必要となる代表的な場合を2つ紹介します。

• 各関節の角度情報からエンドエフェクタの位置座標情報に変換したい場合
• エンドエフェクタの位置座標情報から各関節の角度情報に変換したい場合

上記の場合について具体例として、関節角度を入出力とするロボットと、位置を入出力とする制御器を考えてみます。このとき、ロボットと制御器の入出力形式は異なっているので直接繋ぐことはできません。

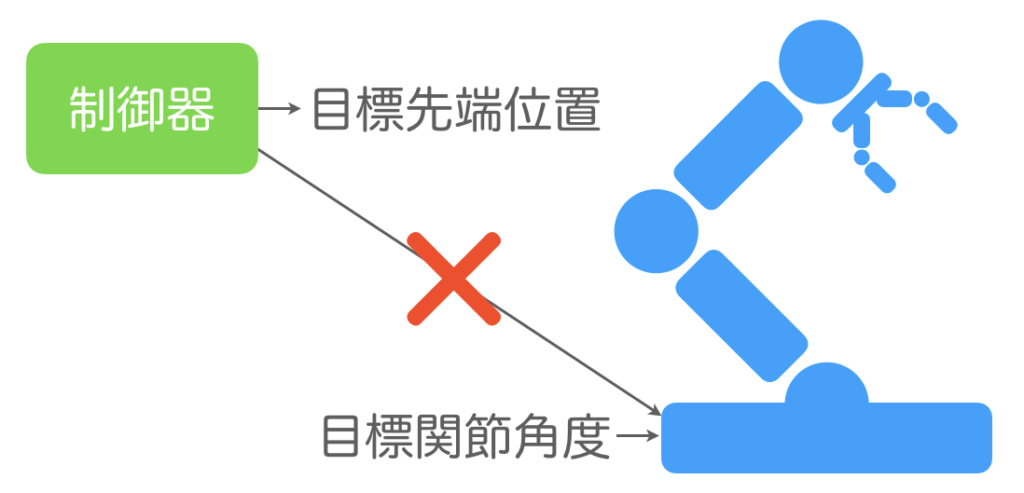
そのため、ロボットと制御器の中間に、エンドエフェクタの位置座標情報と各関節の角度情報を相互に変換するプログラム（=運動学を扱うプログラム）をかます必要があります。

まず、前者の「各関節の角度情報からエンドエフェクタの位置座標情報に変換したい場合」では、ロボットの実機から各関節の角度情報を受け取り、運動学（順運動学）を用いてエンドエフェクタの位置座標情報に変換して制御器に入力します。後者の「エンドエフェクタの位置座標情報から各関節の角度情報に変換したい場合」では、制御器からエンドエフェクタの目標位置座標を受け取り、運動学（逆運動学）を持ちて各関節の角度情報に変換してロボットに入力します。

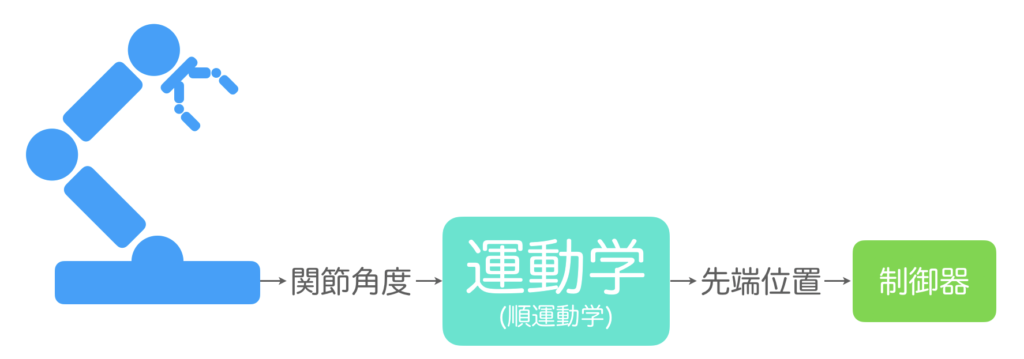
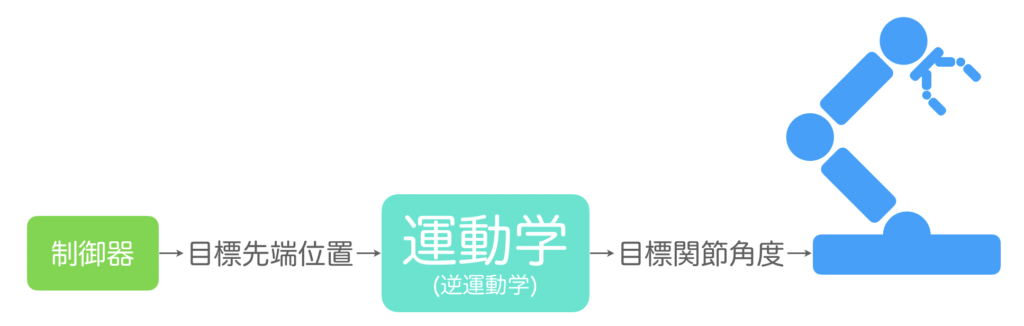
今、ここで紹介した2つの例は、運動学において重要なテーマであり、前者を扱うのを順運動学（Forward Kinematics: FK）、後者を扱うのを逆運動学（Inverse Kinematics: IK）といいます。すなわち、順運動学とはロボットの各関節角度からエンドエフェクタの位置座標および姿勢を求めること、逆運動学とはエンドエフェクタの位置座標および姿勢から各関節角度を求めることです。これらの関係を図に示すと以下のようになります。

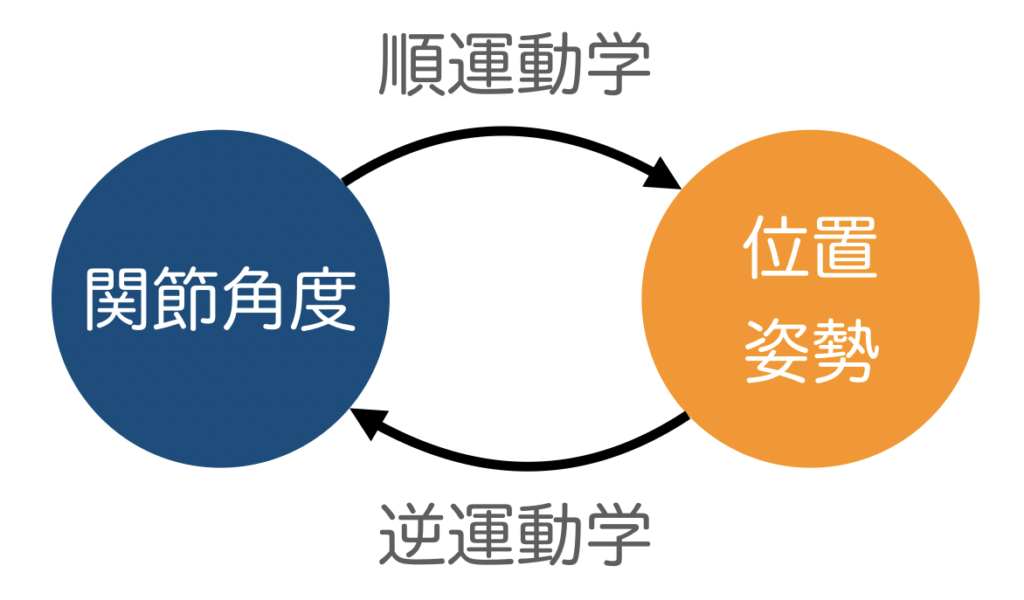
順運動学の導出方法

まず、順運動学を導出する方法として、以下の2つを説明します。

• 図を使う方法
• 同次変換行列を使う方法

図を使う方法

前者は、ロボットの図を描いて、そこに長さ・回転角度の情報を書き込み、そこから三角関数を用いて等式を作成する方法です。後で2自由度マニピュレータの順運動学の例を紹介しますが、そのときに使う図を以下に示します。下図には、ロボットの概略図と、リンクの各種パラメータ（リンクの長さ、回転角度）および、三角関数を用いた各軸方向の長さ情報が書き込まれています。これらの情報と、エンドエフェクタの位置で等式を作ることで順運動学を求めることができます。

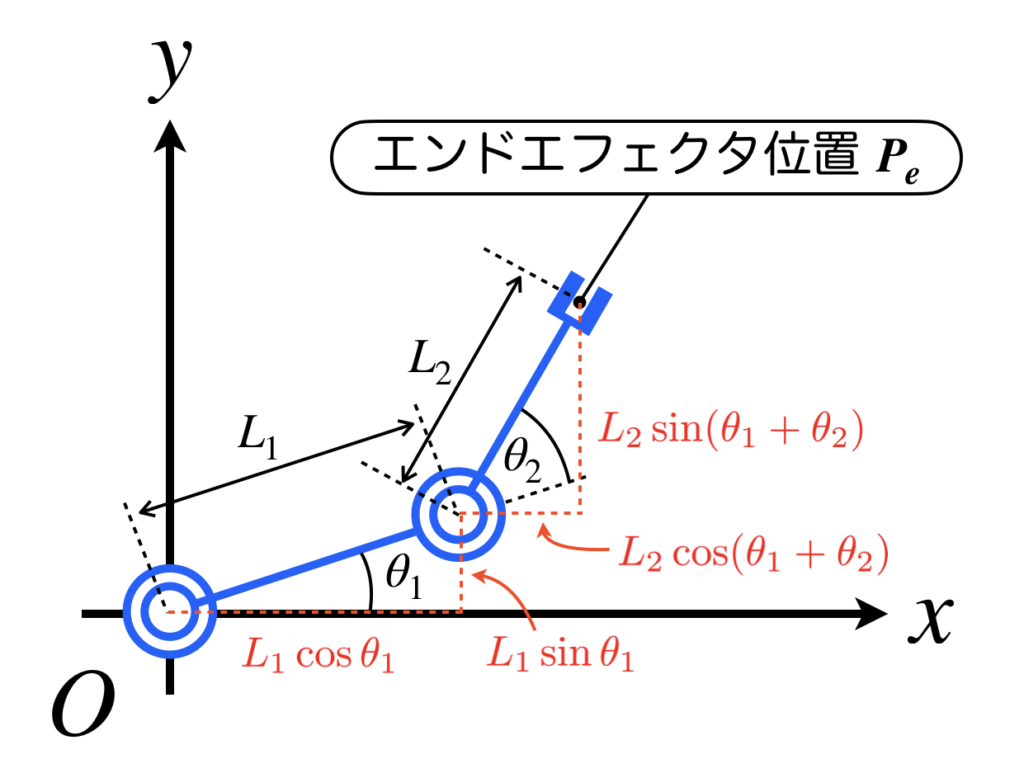
図を用いた順運動学の解法のイメージいただけたと思いますが、この方法は、人間の想像力に委ねられる部分があるため、ロボットの構造が複雑になると式を立てるときに混乱してミスする可能性が高くなるため、賢い解法とはいえません。そのため、より機械的で楽に解く賢い方法が必要となります。それが、2つ目の方法として紹介する同次変換行列を用いる手法です。

同次変換行列を使う方法

同時変換行列を使う方法は、順運動学を機械的に導出することが可能な画期的な方法です。同次変換行列は、コンピュータグラフィックス分野でもよく利用されるので、ロボティクス以外の分野でも使える便利なものです。

同時変換行列を使う方法について説明する前に、先に紹介した図を用いた方法で複雑なロボットの順運動学を導出するときにミスが発生しやすいのは何故かを説明します。結論を言うと、ローカル座標系からワールド座標系へ変換する作業が大変だからです。知らないワードが出てきたかもしれませんが後で説明するのでご安心ください。まず、ロボットに限った話ではありませんが、座標系というのは様々考えられますね。例えば、ロボットの土台を原点とする座標系、ロボットの関節を原点とする座標系、ロボットのエンドポイントを原点とする座標系などです。以下のような単純な2自由度マニピュレータを考えてみます。いくつかの座標系を考える際に、ロボットの基準状態を決めておかないと、動作時の変換を定義できないので、ここでは、ロボットは全関節角度が0の状態を基本状態（下図（上））とすることにします。次に、座標系を複数配置しますが、その座標系を配置すべき位置は、ロボットの土台と関節部分です。そこに座標系を書き込んでみました（下図（下））。書き込んだ座標系は、ロボットの土台、土台に繋がっている関節、2つ目の関節です。これらの座標系について説明の都合上、①〜③まで順番に番号を付与しました。

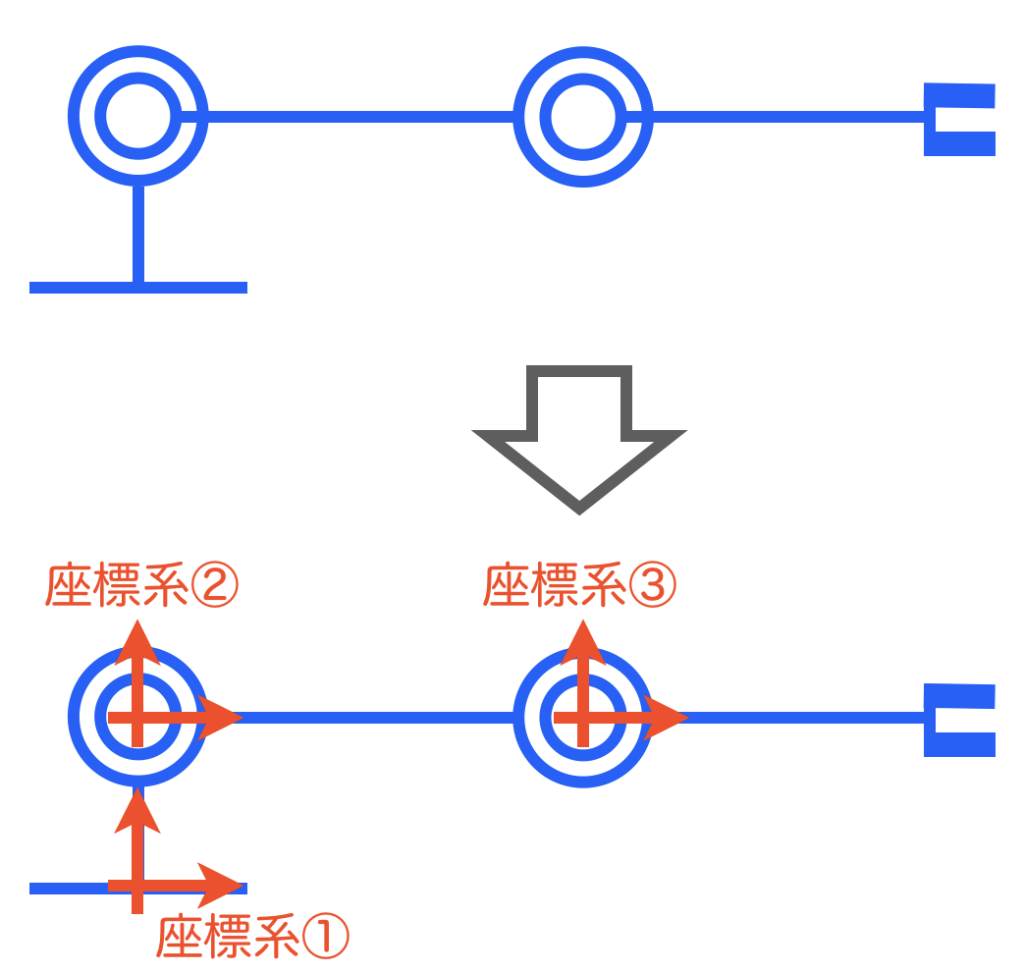
ここで、ロボットが動作して形状が変化したとします。このとき、各座標系は下図のようになります。それぞれの座標系は、ロボットの対応するパーツに付随して位置および姿勢が変化します。位置および姿勢の変化が生じない座標系①は全く変化していません。一方で、それ以外の座標系②と③は、ロボットの動作とともに位置と姿勢が変化しています。

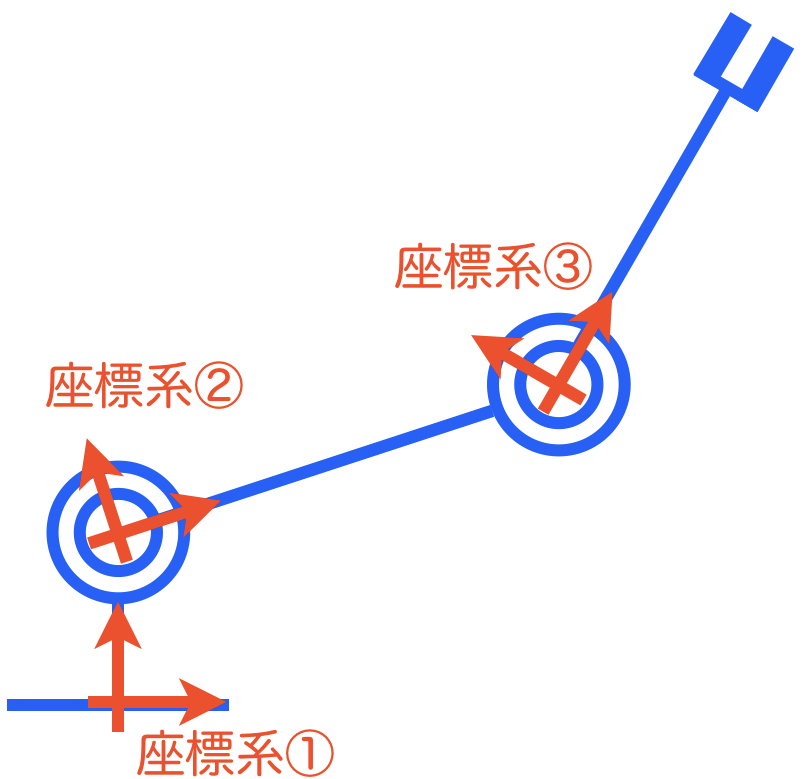
それぞれの座標系の変化について、その現象を細分化し論理的に考えてみることにします。まず、座標系①から見た座標系②の原点位置は動作の前後で変化していませんが、回転（＝姿勢）が変化していますね。座標系①から見た座標系③の原点位置と回転は動作の前後で変化していますね。また、座標系②から見た座標系③の原点位置は動作の前後で変化していませんが回転が変化していますね。

ここで、ある重要な性質に気がつくと思います。それは、動作の前後において、

• 座標系①から見た座標系②の原点位置
• 座標系②から見た座標系③の原点位置

は変化していないことと、変化したのは、

• 座標系①から見た座標系②の回転
• 座標系②から見た座標系③の回転

だけだということです（これは例の場合であり、リンク長が変化するマニピュレータの場合は異なる結果となります）。もちろん、座標系①から見た座標系③の原点位置や回転なども変化していますが、それは、座標系②が回転したことに起因しており本質的ではありません。つまり、座標系に親子関係があり、親の座標系が動けば、子の座標系、そして更に孫の座標系（子の座標系の子の座標系）も動きます。今回の場合、矢印の前を親、矢印の後を子として、以下のような関係になっています。

• 座標系①→座標系②→座標系③

ここで、説明の都合上、最も上位の親を持たない座標系をワールド座標系、それ以外をローカル座標系と呼ぶことにします（ワールド座標系・ローカル座標系というワードはUnityで使われています）。このように定義すると、ワールド座標系は座標系①、ローカル座標系は座標系②③です。このとき、順運動学の導出とは、ワールド座標系におけるエンドエフェクタ位置を求めることとなりますね（座標系③におけるエンドエフェクタの位置座標を座標系①における位置座標に変換する問題）。子の座標系から親の座標系への変換は、平行移動や回転・拡大縮小により実現可能で、まさにこれは同時変換行列を用いればよいので、エンドエフェクタの座標系からワールド座標系に至るまで順番に同時変換行列を求めていけば、それらを掛け合わせる操作のみで順運動学の導出ができます。すなわち、人間の想像力に頼る必要があるのは、親子関係にある座標系の同時変換行列を導出するときのみであり、先ほどの例において、座標系①と②、座標系②と③について考えるだけで良いのです。

先ほど紹介した図を用いた手法では、座標系③におけるエンドエフェクタの位置座標を座標系①における位置座標に頭の中で一気に想像しながら、導き出す必要があったためミスが起こりやすかったのです。

同時変換行列を用いた手法では、局所的な親子関係を考えるだけで良いので、例え100個の自由度があったとしても、問題なく計算することができます。
※それぞれの同時変換行列を求めた後の行列計算は手作業ではなく計算機で行いましょう。

ここまでの説明で、同時変換行列を用いた手法がいかに素晴らしいのか、ご理解いただけたと思います。

とはいえ、同時変換行列というワードを、天下り的に導入したので、次に同時変換行列について解説します。

※同次変換行列を用いて順運動学を導出する方法として、Denavit-Hartenbergの表記法（DH法）という、ちゃんとした方法があるのですが、今回は、イメージ重視で解説しているため、DH法に比べ方法論としての正確性に欠ける可能性があります。より正しい方法を知りたい方は、DH法について調べてみてください。

同時変換行列

同時変換行列とは、同次形式で表された座標ベクトルの並進（平行移動）、拡大縮小、回転を実現することができる変換行列のことです。行列の構造としては下図に示す通りで、拡大縮小および回転を実現する正方行列を左に、並進を実現する列ベクトルを右側に並べ、かつ最下行に最も右の成分のみが1の列ベクトルを加えた正方行列となっています。

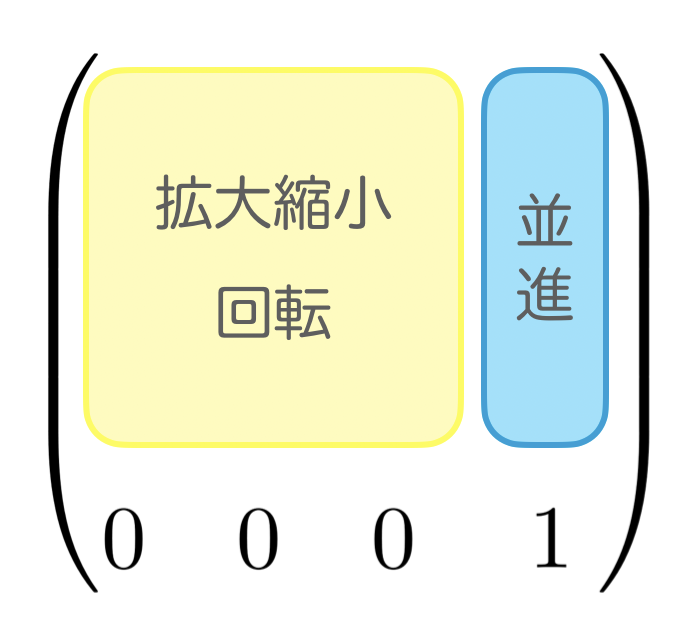
同次変換行列では、N次元座標空間のN次元座標ベクトルに、スカラー値の1を最も下に追加したN+1次元ベクトルによる座標表現（＝同次座標）を用います。例えば、2次元上の座標をベクトルで、

$$\begin{pmatrix} x\\y \end{pmatrix}$$

と表しますが、同次座標では

$$\begin{pmatrix} x\\y\\1 \end{pmatrix}$$

と表します。したがって、N次元ベクトルを変換する同時変換表列はN+1 × N+1行列になります。

ちなみに、同次座標を用いる理由は、並進・拡大縮小・回転を1 つの変換行列で表せるからです。同次座標を用いない場合、並進を拡大縮小および回転と分けて計算する必要があります。
例えば、ベクトル$\begin{pmatrix}x\\y\end{pmatrix}$を、$\begin{pmatrix}a_x\\a_y\end{pmatrix}$だけ並進させ、$\begin{pmatrix}r_{11}&r_{12}\\r_{21}&r_{22}\end{pmatrix}$だけ拡大縮小・回転させる計算は、同次座標を用いない場合、以下のように2ステップの計算処理として実現されます。

$$\begin{pmatrix} x'\\y' \end{pmatrix} = \begin{pmatrix} a_x\\a_y \end{pmatrix} + \begin{pmatrix} r_{11}&r_{12}\\ r_{21}&r_{22} \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}$$

一方で、同次座標を用いた場合では、以下のように1ステップの計算処理で実現できます。

$$\begin{pmatrix} x'\\y'\\1 \end{pmatrix} = \begin{pmatrix} r_{11}&r_{12}&a_x\\ r_{21}&r_{22}&a_y\\ 0&0&1 \end{pmatrix} \begin{pmatrix} x\\y\\1 \end{pmatrix}$$

以上の内容より、同次変換行列による変換と同次座標系について、概要とその便利さをイメージいただけたと思います。

次に、具体的に知っておくと便利な同次変換行列について、2次元空間の変換で使用する3x3の同次変換行列と、3次元空間の変換で使用する4x4の同次変換行列に焦点を絞って紹介していきます。

2次元座標系の変換で使用する同次変換行列

並進

2次元ベクトル空間上の点$\boldsymbol{P}=(P_x, P_y)^T$を$\boldsymbol{M}=(M_x, M_y)^T$だけ移動させることを考えます。このとき、$\boldsymbol{M}$だけ移動させる同次変換行列$T_M$を以下のようにして定義します。

$$T_M = \begin{pmatrix} 1 & 0 & M_x \\ 0 & 1 & M_y \\ 0 & 0 & 1 \end{pmatrix}$$

この同次変換行列を使って、点$\boldsymbol{P}$の移動先を以下のようにして求めることができます。

$$T_M\begin{pmatrix}\boldsymbol{P}\\1\end{pmatrix}$$

実際に計算して確かめてみましょう。

$$\begin{eqnarray} T_M\begin{pmatrix}\boldsymbol{P}\\1\end{pmatrix} &=& \begin{pmatrix} 1 & 0 & M_x \\ 0 & 1 & M_y \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}P_x\\P_y\\1\end{pmatrix}\\ &=&\begin{pmatrix}P_x + M_x\\P_y+M_y\\1\end{pmatrix} \end{eqnarray}$$

ここでは、まだ同次座標を考えているので、該当部分から2次元ベクトルを抜き出すと結果は以下のようになります。

$$\begin{pmatrix}P_x + M_x\\P_y+M_y\end{pmatrix}$$

拡大縮小

2次元ベクトル空間上の点$\boldsymbol{P}=(P_x, P_y)^T$を、$x$軸方向に$a$倍、$y$軸方向に$b$倍することを考えます。このとき、同次変換行列$T_S$を以下のようにして定義します。

$$T_S = \begin{pmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

この同次変換行列を使って、点$\boldsymbol{P}$の移動先を以下のようにして求めることができます。

$$T_S\begin{pmatrix}\boldsymbol{P}\\1\end{pmatrix}$$

実際に計算して確かめてみましょう。

$$\begin{eqnarray} T_S\begin{pmatrix}\boldsymbol{P}\\1\end{pmatrix} &=& \begin{pmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}P_x\\P_y\\1\end{pmatrix}\\ &=&\begin{pmatrix}aP_x\\bP_y\\1\end{pmatrix} \end{eqnarray}$$

同次座標から目的の座標を抜き出すと以下のようになります。

$$\begin{pmatrix}aP_x\\bP_y\end{pmatrix}$$

回転

2次元ベクトル空間上の点$\boldsymbol{P}=(P_x, P_y)^T$を、角度$\theta$だけ回転させることを考えます。このとき、同次変換行列$T_R$を以下のようにして定義します。

$$T_R = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix}$$

この同次変換行列を使って、点$\boldsymbol{P}$の移動先を以下のようにして求めることができます。

$$T_R\begin{pmatrix}\boldsymbol{P}\\1\end{pmatrix}$$

実際に計算して確かめてみましょう。

$$\begin{eqnarray} T_R\begin{pmatrix}\boldsymbol{P}\\1\end{pmatrix} &=& \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}P_x\\P_y\\1\end{pmatrix}\\ &=&\begin{pmatrix}P_x\cos\theta - P_y\sin\theta\\P_x\sin\theta + P_y\cos\theta\\1\end{pmatrix} \end{eqnarray}$$

同次座標から目的の座標を抜き出すと以下のようになります。

$$\begin{pmatrix}P_x\cos\theta - P_y\sin\theta\\P_x\sin\theta + P_y\cos\theta\end{pmatrix}$$

具体例

上で説明した内容と、順運動学の導出をイメージしてもらうために、簡単な例題に取り組んでみましょう。

[例題] 座標系①と座標系②の座標系があります。座標系②における青点の座標は$\begin{pmatrix}L_2\cos\theta_2\\L_2\sin\theta_2\end{pmatrix}$と表されます。また、座標系②は、座標系①を$\begin{pmatrix}L_1\cos\theta_1\\L_1\sin\theta_1\end{pmatrix}$だけ並進し、角度$\theta_1$だけ回転させたものと一致します。このとき、座標系①における青点の座標はどのように表されるでしょうか？

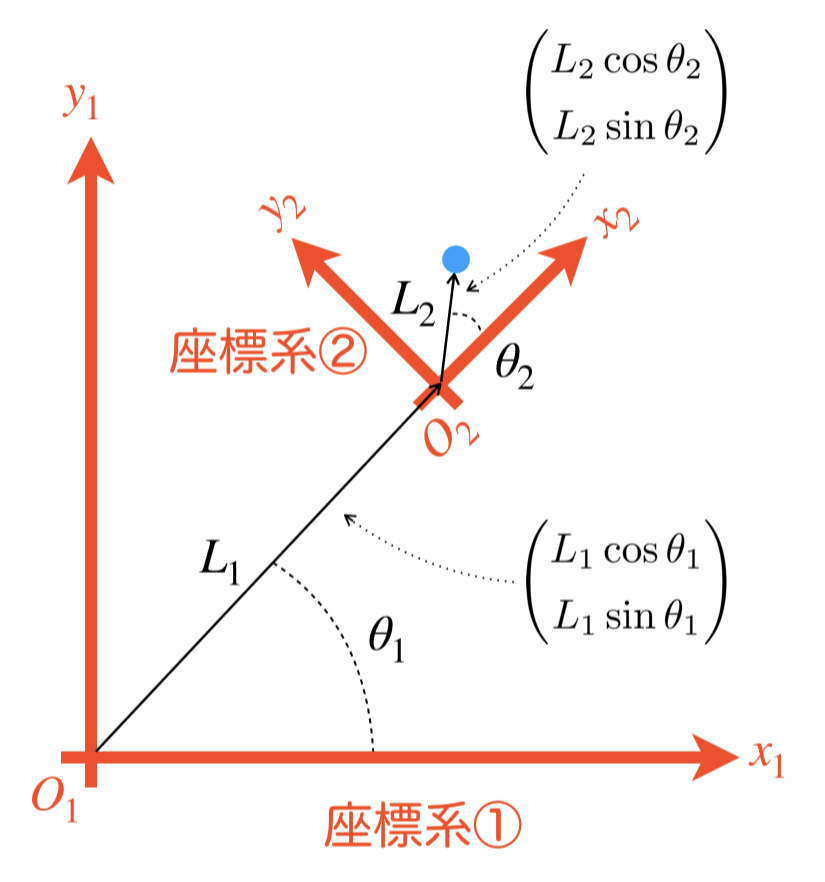
答えは、以下の通りで、座標系①から見た座標系②についての同次変換行列を作り、座標系②における青点の同次座標ベクトルをかけることで導出されます。

※この例題は、図を使う解法でも容易に導出できます。ここでは、省略しますが、興味があれば試しでみてください。

3次元座標系の変換で使用する同時変換行列

3次元座標系の変換で使用する同次変換行列も、2次元の場合と考え方は同じなので、結果だけ紹介します。

並進

3次元ベクトル空間上の点を$\boldsymbol{M}=(M_x, M_y, M_z)^T$だけ移動させる同次変換行列$T_M$は以下の通りです。

$$T_M = \begin{pmatrix} 1 & 0 & 0 & M_x \\ 0 & 1 & 0 & M_y \\ 0 & 0 & 1 & M_z \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

拡大縮小

3次元ベクトル空間上の点を、$x$軸方向に$a$倍、$y$軸方向に$b$倍、$z$軸方向に$c$倍する同次変換行列$T_S$は以下の通りです。

$$T_S = \begin{pmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

回転

• $x$軸まわりの回転

$$T_{R_x} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta_x & -\sin\theta_x & 0 \\ 0 & \sin\theta_x & \cos\theta_x & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

• $y$軸まわりの回転

$$T_{R_y} = \begin{pmatrix} \cos\theta_y & 0 & \sin\theta_y & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta_y & 0 & \cos\theta_y & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

• $z$軸まわりの回転

$$T_{R_z} = \begin{pmatrix} \cos\theta_z & -\sin\theta_z & 0 & 0 \\ \sin\theta_z & \cos\theta_z & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

逆運動学の導出方法

ここまで、順運動学の導出方法として、図を用いた解法と同次変換行列を用いた解法について多くの分量を割いて説明しました。これには理由があり、逆運動学を導出する前の作業として順運動学を導出する必要があるからです。順運動学も逆運動学も、式を導出するという点においては同じですが、導出の容易さが全く異なります。順運動学は図や同次変換行列を用いて位置に関する関係式を作ることで、直接、関節角度からエンドエフェクタ位置へ変換する式を導出できますが、逆運動学は、図形的な難度がとても高く、直接、エンドエフェクタ位置から関節角度へ変換する式を求めることはできません。そのため、まず順運動学を導出し、その式を連立方程式として関節角度について解くことで導出します。すなわち、逆運動学では図形的な情報はほぼ使用せず順運動学で導出した式の連立方程式を関節角度について解くことで導出します。関節角度に関して連立方程式を解ければ逆運動学の導出は完了するのです。では、どうやって導出するのかを説明するのが次の内容です。

その方法には、解析的解法と、数値的解法があります。解析的解法とは、複雑さの低い順運動学を手作業なりで解いて、直接、関節角度について導出する方法です。しかし、複雑さが高くなると、そもそも導出することが困難になります。そこで、近似的に解く方法として数値的解法がとられます。解析的解法では、式変形や三角関数の性質を駆使して関節角度について解くだけでなので、高校数学レベルの知識がある方であれば、特に説明は必要ないのですが、一部、紹介しておきたい項目があるので簡単に解説します。また、数値的解法は応用的な内容なので簡単な紹介にとどめることとします。

解析的解法

逆三角関数の値域

解析的解法は、順運動学で導出した式を連立方程式として、各関節角度について解く方法です。自由度が3つ程度までなら、手作業でも求めることが可能です。その際に、アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を使用しますが、その範囲について注意が必要です。逆三角関数は、値域に範囲指定がないと無限個の解が求まってしまうため、以下のように値域が設定されています。

アークサイン（$sin^{-1}$）	アークコサイン（$cos^{-1}$）	アークタンジェント（$tan^{-1}$）
$-\frac{\pi}{2}\le \theta \le \frac{\pi}{2}$	$0\le \theta \le \pi$	$-\frac{\pi}{2}< \theta < \frac{\pi}{2}$

プログラムで逆三角関数を使用する場合の返り値は、上記の範囲となります。そこで問題となるのが、ロボットの関節の稼働範囲は$pi$の範囲内に収まるとは限らないということです。せめて、1周分（$2\pi$）、は対応できないと困ります。

そこで使用されるのが、次に説明するアークタンジェント2（atan2）です。

アークタンジェント2

アークタンジェントを含む逆三角関数は傾きを求めるために使用します。一方で、アークタンジェント2は偏角（arg）を求めるために使用します。例えば、下図の左右の青点を結んだ線の傾きは、どちらも傾きは45度ですが、偏角は左が45度で右が225度です。すなわち、偏角の方が傾きよりも関節角度を表現するのに適しているのです。

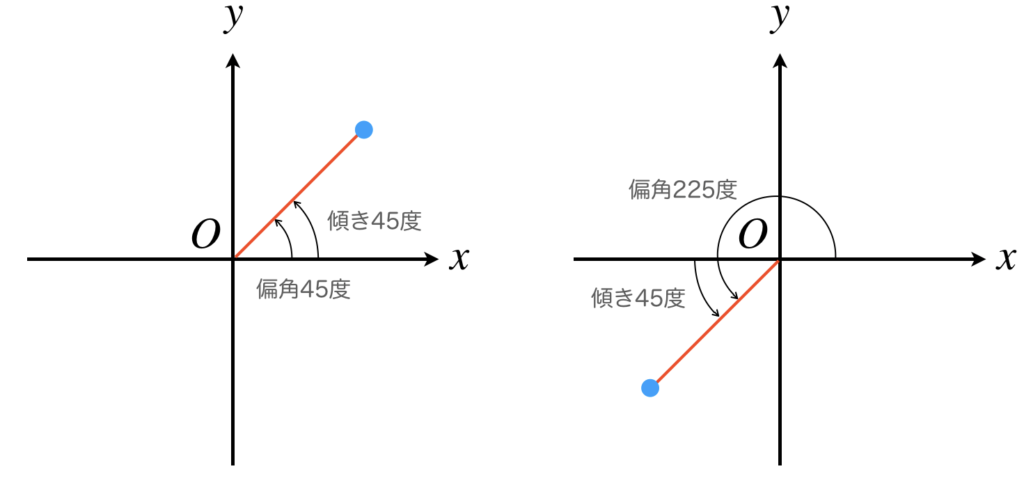
アークタンジェントの値域は先に示した通り$-\frac{\pi}{2}< \theta < \frac{\pi}{2}$ですが、アークタンジェント2の値域は$-\pi< \theta \le \pi$となります。偏角は、$arg(x + iy)$と表されるので、アークタンジェント2には2つの引数$(x, y)$が必要となります。引数の順番としては、$atan2(y, x)$となることが多いですが、言語やライブラリによっては順番が異なる場合があります。

UnityのC#やPythonなど、多くのプログラムでatan2が提供されているので、使用する際は、公式ドキュメント等を参考に引数の順番等を確認することをお勧めします。

数値的解法

解析的解法は関節が多いロボットにおける逆運動学の導出に使用できないので、その場合には、数値的に近似解を求める方法が取られます。数値的に解く方法は様々ありますが、ヤコビアンを用いた解法がよく用いられます。数値的解法については、以降の例でも扱わないので、この程度の説明にとどめることにします。今後、ヤコビアンによる逆運動学の導出について、別途、記事を作成するかもしれませんので、作成したときは、ここにリンクを貼ります。

2自由度マニピュレータの運動学

ここまで説明した内容を踏まえて、具体的な問題として、2自由度のマニピュレータの運動学について解説します。

※この後に3自由度のマニピュレータの運動学についても説明します。

問題設定

具体例を用いて、順運動学と逆運動学の求め方を紹介します。

以下のような2自由度のアームを考えます。2つのリンクがあり各リンクの長さは付け根から順番に$L_1$、$L_2$で、各関節角度は付け根から順番に$\theta_1$、$\theta_2$とします。また、エンドエフェクタの位置を$\boldsymbol{P_e}(x_e, y_e)$とします。

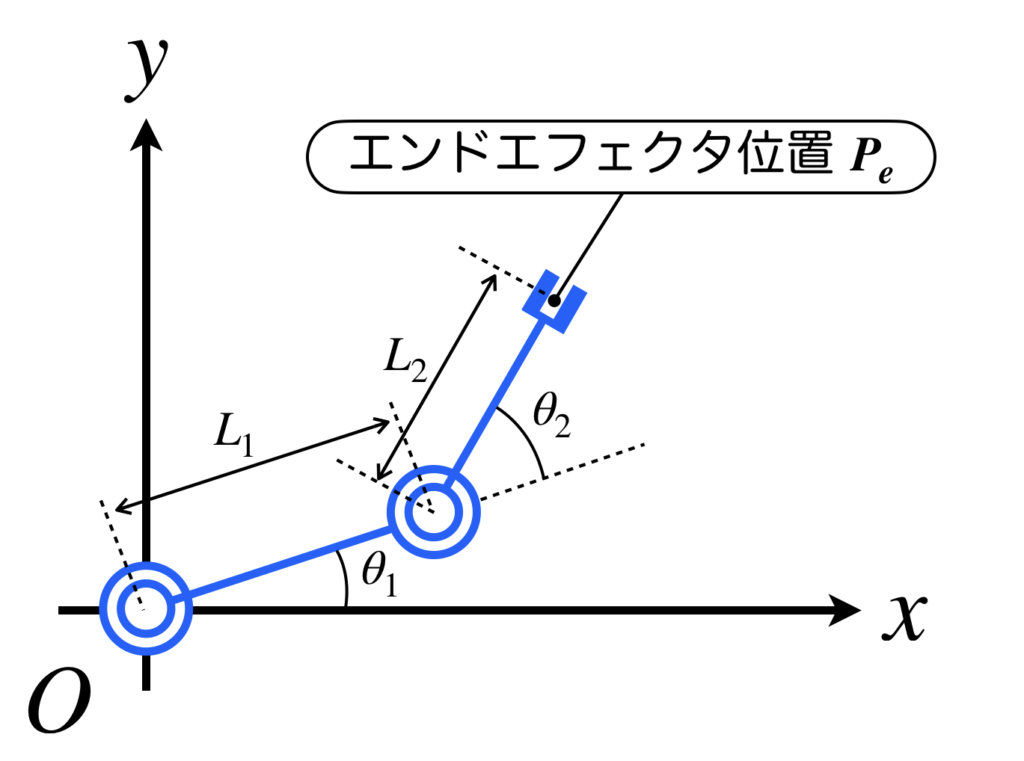
順運動学の導出

まず、順運動学を導出します。方向性としては、$\boldsymbol{P_e}(x_e, y_e)$をリンクの長さと関節角度で表すことです。

図を用いた解法

問題設定が簡単なので、図を用いた方法で容易に導出することができます。

長さが$L_1$のリンクが角度$\theta_1$だけ回転した状態のとき、$x$軸方向の長さは$L_1\cos\theta_1$、$y$軸方向の長さは$L_1\sin\theta_1$です。長さが$L_2$のリンクがリンク1に対して角度$\theta_2$だけ回転した状態のとき、$x$軸方向の長さは$L_2\cos(\theta_1+\theta_2)$、$y$軸方向の長さは$L_1\sin(\theta_1+\theta_2)$です。これらを用いて、$\boldsymbol{P_e}(x_e, y_e)$と等式を作ると以下のようになります。

$$\left\{ \begin{array}{ccc} x_e &=& L_1\cos\theta_1 + L_2\cos(\theta_1 + \theta_2) \\ y_e &=& L_1\sin\theta_1 + L_2\sin(\theta_1 + \theta_2) \\ \end{array} \right.$$

同次変換行列を用いた解法

もう1つの導出方法である、同次変換行列を用いた方法でも導出してみます。

同次変換行列を用いた場合は、図に書き込む必要はなく、アームの付け根部分から順番に座標系の回転や平行移動などを行う同次変換行列を求めて、順番に行列の掛け算を行うだけで求まります。

$$\begin{eqnarray} &&\begin{pmatrix} \cos\theta_1 & -\sin\theta_1 & 0\\ \sin\theta_1 & \cos\theta_1 & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & L_1\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos\theta_2 & -\sin\theta_2 & 0\\ \sin\theta_2 & \cos\theta_2 & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} L_2\\ 0\\ 1 \end{pmatrix}\\ &=& \begin{pmatrix} L_1\cos\theta_1 + L_2\cos(\theta_1 + \theta_2)\\ L_1\sin\theta_1 + L_2\sin(\theta_1 + \theta_2)\\ 1 \end{pmatrix} \end{eqnarray}$$

結果が同次座標で得られました。

$$\left\{ \begin{array}{ccc} x_e &=& L_1\cos\theta_1 + L_2\cos(\theta_1 + \theta_2) \\ y_e &=& L_1\sin\theta_1 + L_2\sin(\theta_1 + \theta_2) \\ \end{array} \right.$$

なぜ、このような式が出てくるのかを簡単にイメージして頂けるように説明します。先ほどの式変形では、4つの同次変換行列を用いているますが、それぞれ、以下の図に示すような座標系の変換を行なっています。まず、基本座標系（図中：黒）と変換後の座標系（図中：灰色背景に白）があります。Unityなどでは前者をワールド座標系、後者をローカル座標系と呼んでいますね。ここで、同次変換行列を適用すると、ローカル座標系からワールド座標系の座標に変換することができます。

一番左の状態では、同次変換行列による変換が適用されていないため、ワールド座標系とローカル座標系が同じです。
ここで、$z$軸周りに$\theta_1$だけ回転させる回転行列を適用すると、ローカル座標系が左から2つ目の図のようになります。このローカル座標系からみて、$L_1$の長さのリンクは、$x$軸正方向に伸びているので、$x$軸方向に$L_1$だけ平行移動を行う同次変換行列（左から2つ目の行列）を適用して、ローカル座標系をさらに並行移動します。これを繰り返し行い、エンドエフェクタが固定されているリンクの関節点まで座標系を移動させます。そして、その座標から見たエンドエフェクタの座標ベクトルを求めます。

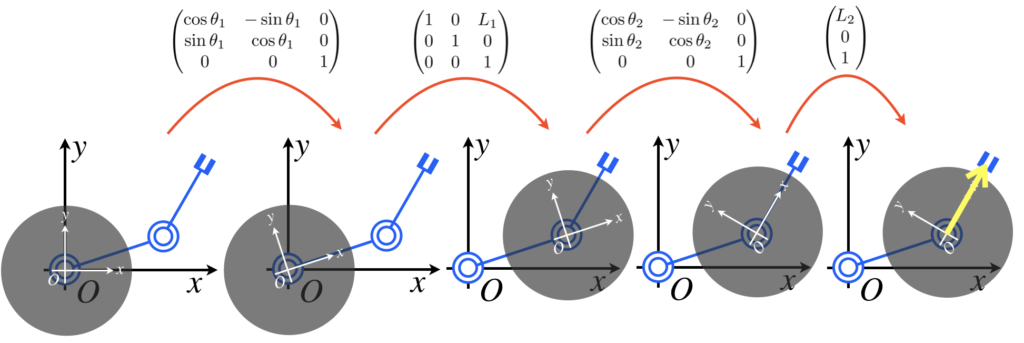
これの何が嬉しいかというと、これらの変換を行う同次変換行列を計算すると、一番右側の列ベクトルを掛けるだけで、ワールド座標からみたときの同次座標が得られるのです。

※同次変換行列を用いて順運動学を導出する方法として、Denavit-Hartenbergの表記法（DH法）という、ちゃんとした方法があるのですが、今回は、イメージ重視で解説しているため、DH法に比べ方法論としての正確性に欠ける可能性があります。より正しい方法を知りたい方は、DH法について調べてみてください。

逆運動学の導出

ここでは、先ほどの導出した順運動学（以下）を用いて、逆運動学を解いていきます。

逆運動学は、解に制約を課さないと一意に定まらないため、$0\le\theta_2\le\pi$という制約を課すこととします。

$$\left\{ \begin{array}{ccc} x_e &=& L_1\cos\theta_1 + L_2\cos(\theta_1 + \theta_2) \\ y_e &=& L_1\sin\theta_1 + L_2\sin(\theta_1 + \theta_2) \\ \end{array} \right.$$

それぞれの式を2乗して足してみます。

$$\begin{eqnarray} x_e^2 + y_e^2 &=& L_1^2\cos^2\theta_1 + 2L_1L_2\cos\theta_1\cos(\theta_1+\theta_2) + L_2^2\cos^2(\theta_1 + \theta_2)\\ && + L_1^2\sin^2\theta_1 + 2L_1L_2\sin\theta_1\sin(\theta_1+\theta_2) + L_2^2\sin^2(\theta_1 + \theta_2)\\ &=& L_1^2 + L_2^2 + 2L_1L_2\cos\theta_2 \end{eqnarray}$$

となるので、

$$\cos\theta_2 = \frac{x_e^2 + y_e^2 - L_1^2 - L_2^2}{2L_1L_2}$$

となり、

$$\theta_2 = \pm\cos^{-1}\left(\frac{x_e^2 + y_e^2 - L_1^2 - L_2^2}{2L_1L_2}\right)$$

となります。この時点では、±がついていることに注意してください。ここで、$0\le\theta_2\le\pi$という条件を与えることで、以下のように一意に決定することができます。

$$\theta_2 = \cos^{-1}\left(\frac{x_e^2 + y_e^2 - L_1^2 - L_2^2}{2L_1L_2}\right)$$

次に、$\theta_1$を求めます。順運動学で求めた2式を、以下のように変形して、両辺を2乗し足してみます。

$$\left\{ \begin{array}{ccc} x_e - L_1\cos\theta_1 &=& L_2\cos(\theta_1 + \theta_2) \\ y_e - L_1\sin\theta_1&=& L_2\sin(\theta_1 + \theta_2) \\ \end{array} \right.$$

両辺を2乗して足すと、

$$x_e^2 + y_e^2 - 2L_1\sqrt{x_e^2 + y_e^2}\cos\left(\theta_1 - \tan^{-1}\frac{y_e}{x_e}\right) + L_1^2= L_2^2$$

となります。したがって、

$$\cos\left(\theta_1 - \tan^{-1}\frac{y_e}{x_e}\right) = \frac{L_1^2 + x_e^2 + y_e^2 - L_2^2}{2L_1\sqrt{x_e^2 + y_e^2}}$$

となります。この時点では、

$$\theta_1 = \tan^{-1}\frac{y_e}{x_e} \pm \cos^{-1}\left(\frac{L_1^2 + x_e^2 + y_e^2 - L_2^2}{2L_1\sqrt{x_e^2 + y_e^2}}\right)$$

ここで、$0\le\theta_2\le\pi$という条件のもと、この問いのマニピュレータが幾何学的に成立するのは、

$$\theta_1 = \tan^{-1}\frac{y_e}{x_e} - \cos^{-1}\left(\frac{L_1^2 + x_e^2 + y_e^2 - L_2^2}{2L_1\sqrt{x_e^2 + y_e^2}}\right)$$

となります。

※今回の解き方の場合、両方の解を求める際に解の選択が生じましたが、この問題は、どちらか一方の解の範囲を決定してしまえば、自ずともう一方の解も決まる問題なので、もっと賢い解き方を知りたい方はネットを漁ってみてください。

ちなみに、もし値の範囲に指定がなければ、以下のような解答が正解となるでしょう。

$$\begin{eqnarray} \theta_1 &=& \tan^{-1}\frac{y_e}{x_e} \pm \cos^{-1}\left(\frac{L_1^2 + x_e^2 + y_e^2 - L_2^2}{2L_1\sqrt{x_e^2 + y_e^2}}\right)\\ \theta_2 &=& \mp \cos^{-1}\left(\frac{x_e^2 + y_e^2 - L_1^2 - L_2^2}{2L_1L_2}\right) &&(符号同順) \end{eqnarray}$$

3自由度マニピュレータの運動学

次に、3自由度マニピュレータの運動学を解いてみます。

問題設定

下図に示す3自由度マニピュレータを考えます。各関節の位置やリンクの長さは図に記載した通りとします。

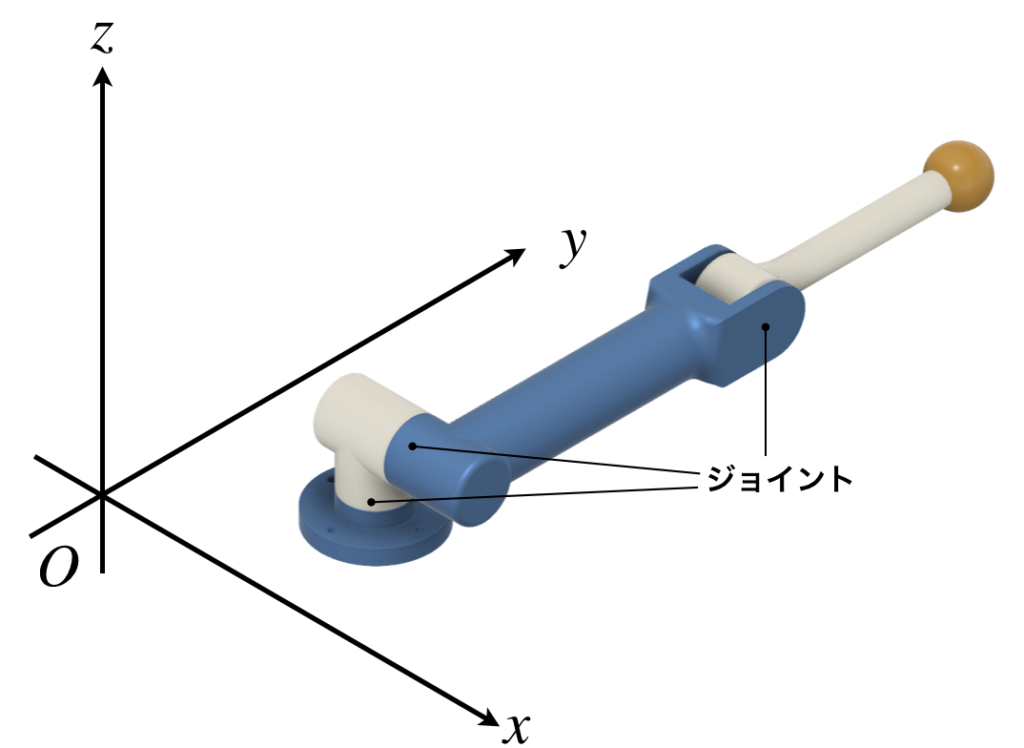
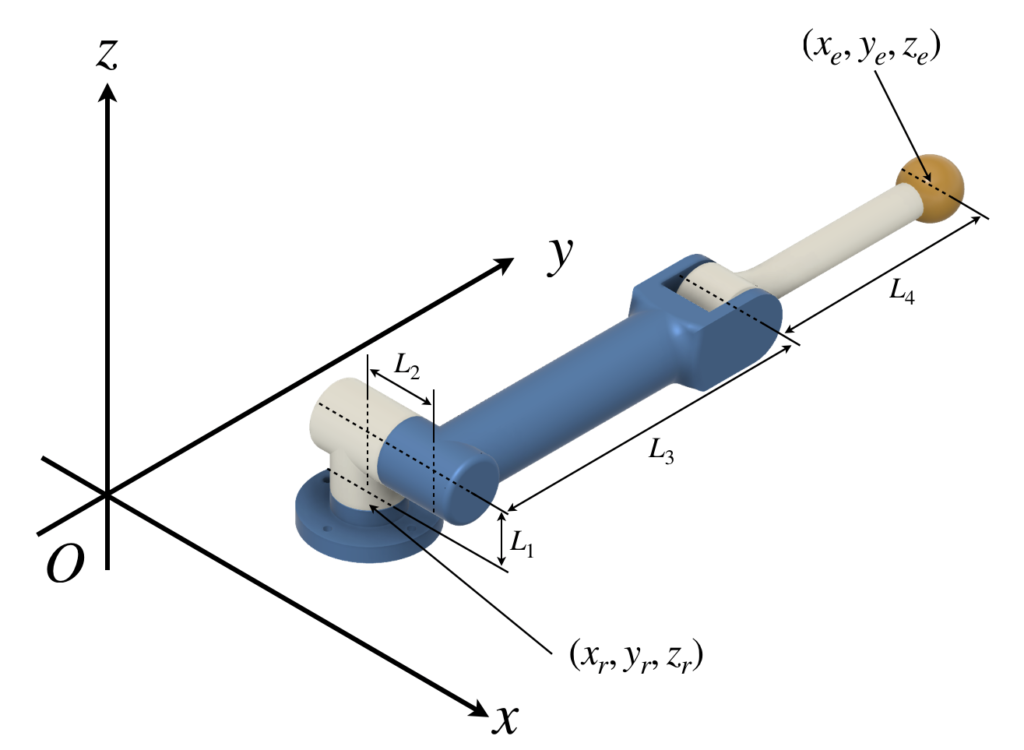
3つの関節のうち、土台に固定されている関節の位置を$(x_r, y_r, z_r)$、エンドエフェクタの位置を$(x_e, y_e, z_e)$とします。また、全ての関節が0の時のロボットの形状は、上記の記載の通りとします。

ここで、ロボットが動作し、土台の関節から順番に、$\theta_1, \theta_2, \theta_3$の角度になって停止したとします。

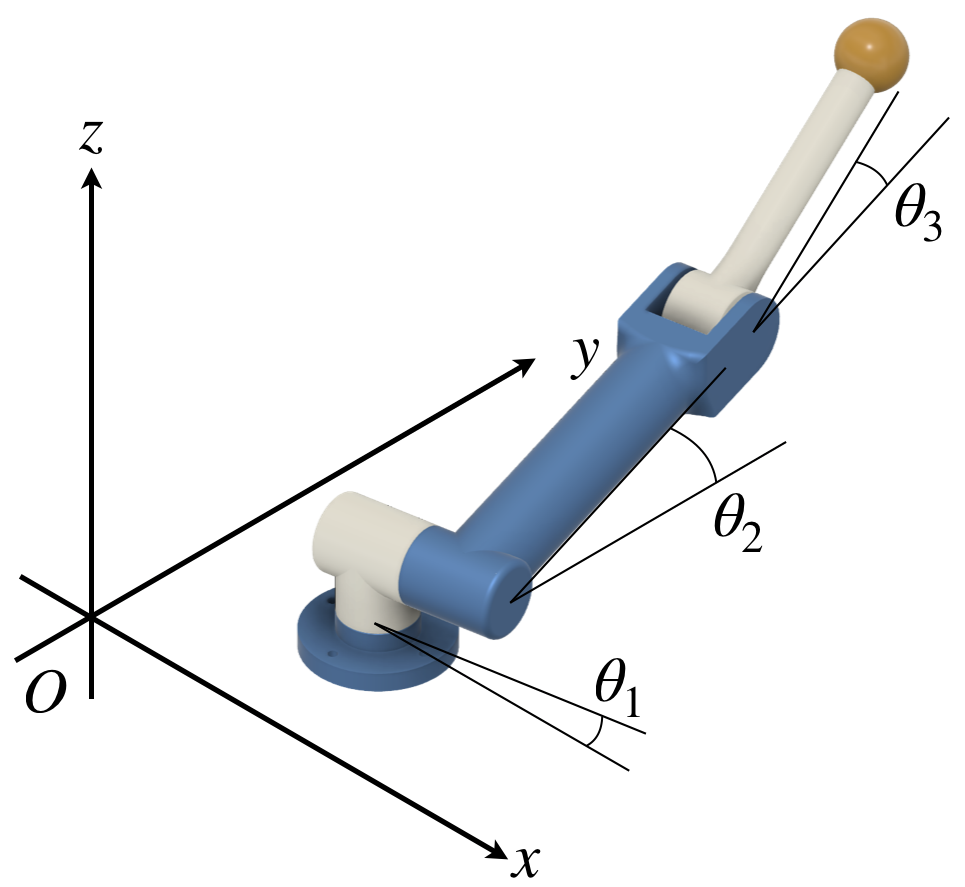
このときの順運動学と逆運動学を導出してみてください。

また、以下の制約を課すこととします。

• $0 \le \theta_3 \le \pi$

順運動学の導出

この問題では、同次変換行列による手法のみを示します。

$$\begin{eqnarray} &&\begin{pmatrix} 1 & 0 & 0 & x_r \\ 0 & 1 & 0 & y_r \\ 0 & 0 & 1 & z_r \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos\theta_1 & -\sin\theta_1 & 0 & 0 \\ \sin\theta_1 & \cos\theta_1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & L_1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & L_2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta_2 & -\sin\theta_2 & 0 \\ 0 & \sin\theta_2 & \cos\theta_2 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & L_3 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta_3 & -\sin\theta_3 & 0 \\ 0 & \sin\theta_3 & \cos\theta_3 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0 \\ L_4 \\ 0 \\ 1 \end{pmatrix}\\ &=&\begin{pmatrix} x_r + L_2\cos\theta_1-L_3\sin\theta_1\cos\theta_2-L_4\sin\theta_1\cos(\theta_2+\theta_3) \\ y_r + L_2\sin\theta_1+L_3\cos\theta_1\cos\theta_2+L_4\cos\theta_1\cos(\theta_2+\theta_3) \\ z_r + L_1+L_3\sin\theta_2+L_4\sin(\theta_2+\theta_3) \\ 1 \end{pmatrix} \end{eqnarray}$$

以上より、

$$\left\{ \begin{array}{rcl} x_e &=& x_r + L_2\cos\theta_1-L_3\sin\theta_1\cos\theta_2-L_4\sin\theta_1\cos(\theta_2+\theta_3) \\ y_e &=& y_r + L_2\sin\theta_1+L_3\cos\theta_1\cos\theta_2+L_4\cos\theta_1\cos(\theta_2+\theta_3) \\ z_e &=& z_r + L_1+L_3\sin\theta_2+L_4\sin(\theta_2+\theta_3) \end{array} \right.$$

が図の3自由度マニピュレータの順運動学になります。

逆運動学の導出

上で求めた順運動学を再掲します。

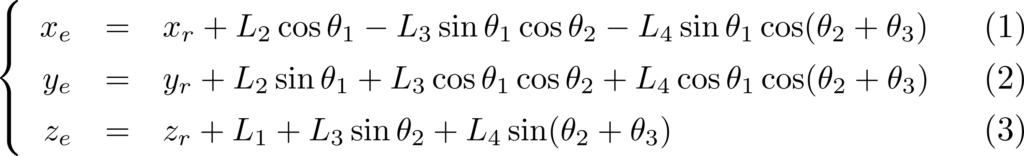
ここから、関節角度$\theta_1, \theta_2, \theta_3$を導出していきます。

導出には、幾つかの方法が考えられますが、今回は、以下のような手順で計算していくことにします。

1. $((1) - x_r)^2 + ((2) - y_r)^2$から$\theta_2$と$\theta_3$のみの式(4)を作る
2. 式(3)と式(4)から$\theta_3$を導出する
3. 2で導出した$\theta_3$と式(3)から$\theta_2$を導出する
4. 2と3で求めた$\theta_2, \theta_3$と式(1)から$\theta_1$を導出する

以下では、上の手順に従って順番に進めていきます。

手順1

$((1) - x_r)^2 + ((2) - y_r)^2$から$\theta_2$と$\theta_3$のみの式(4)を導出します。

$$\begin{eqnarray} &&((1) - x_r)^2 + ((2) - y_r)^2 \\ &=& (x_e - x_r)^2 + (y_e - y_r)^2\\ &=& L_2^2 + L_3^2\cos^2\theta_2 + L_4^2\cos^2(\theta_2 + \theta_3) + 2L_3L_4\cos\theta_2\cos(\theta_2 + \theta_3) \end{eqnarray}$$

計算過程は省略していますが、以上の計算式より、式(4)は

$$(x_e - x_r)^2 + (y_e - y_r)^2 = L_2^2 + L_3^2\cos^2\theta_2 + L_4^2\cos^2(\theta_2 + \theta_3) + 2L_3L_4\cos\theta_2\cos(\theta_2 + \theta_3)$$

です。

手順2

式(3)と式(4)から$\theta_3$を導出します。

ここでは、$(4) + ((3) - z_r - L_1)^2$を求めてみます。

$$\begin{eqnarray} && (4) + ((3) - z_r - L_1)^2 \\ &=& (x_e - x_r)^2 + (y_e - y_r)^2 + (z_e - z_r - L_1)^2\\ &=& L_2^2 + L_3^2\cos^2\theta_2 + L_4^2\cos^2(\theta_2 + \theta_3) + 2L_3L_4\cos\theta_2\cos(\theta_2 + \theta_3) && + L_3^2 \sin\theta_2 + 2L_3L_4\sin\theta_2\sin(\theta_2+\theta_3) + L_4^2\sin^2(\theta_2+\theta_3) \\ &=& L_2^2 + L_3^2 + L_4^2 + 2L_3L_4\cos\theta_3 \end{eqnarray}$$

以上より、

$$\theta_3 = \pm \cos^{-1}\left(\frac{(x_e - x_r)^2 + (y_e - y_r)^2 + (z_e - z_r - L_1)^2 - L_2^2 - L_3^2 - L_4^2}{2L_2L_3}\right)$$

ここで、$0 \le \theta_3 \le \pi$という制約を課すことで、

$$\theta_3 = \cos^{-1}\left(\frac{(x_e - x_r)^2 + (y_e - y_r)^2 + (z_e - z_r - L_1)^2 - L_2^2 - L_3^2 - L_4^2}{2L_2L_3}\right)$$

に決定することができる。

手順3

手順2で導出した$\theta_3$と式(3)から$\theta_2$を導出します。ここでは、いくつか複雑な式変形が必要となるので、途中式も示しました。

$$\begin{eqnarray} z_e &=& z_r + L_1 + L_3\sin\theta_2 + L_4\sin(\theta_2 + \theta_3)\\ &=& z_r + L_1 + L_3\sin\theta_2 + L_4\sin\theta_2\cos\theta_3 + L_4\cos\theta_2\sin\theta_3\\ &=& z_r + L_1 + (L_3 + L_4\cos\theta_3)\sin\theta_2 + L_4\cos\theta_2\sin\theta_3 \\ &=& z_r + L_1 + \sqrt{(L_3 + L_4\cos\theta_3)^2 + L_4^2\sin^2\theta_3}\sin\left(\theta_2 + \tan^{-1}\left(\frac{L_4\sin\theta_3}{L_3 + L_4\cos\theta_3}\right)\right)\\ &=& z_r + L_1 + \sqrt{(x_e - x_r)^2 + (y_e - y_r)^2 + (z_e - z_r - L_1)^2 - L_2^2}\sin\left(\theta_2 + \tan^{-1}\left(\frac{L_4\sin\theta_3}{L_3 + L_4\cos\theta_3}\right)\right) \end{eqnarray}$$

以上より、

$$\theta_2 = \sin^{-1}\left(\frac{z_e - z_r - L_1}{\sqrt{(x_e - x_r)^2 + (y_e - y_r)^2 + (z_e - z_r - L_1)^2 - L_2^2}}\right) - \tan^{-1}\left(\frac{L_4\sin\theta_3}{L_3 + L_4\cos\theta_3}\right)$$

となります。

手順4

手順2と手順3で求めた$\theta_2, \theta_3$と式(1)から$\theta_1$を導出する

$$\begin{eqnarray} x_e &=& x_r + L_2\cos\theta_1 - L_3\sin\theta_1\cos\theta_2 - L_4\sin\theta_1\cos(\theta_2 + \theta_3) \\ &=& x_r + L_2\cos\theta_1 - L_3\sin\theta_1\cos\theta_2 - L_4\sin\theta_1(\cos\theta_2\cos\theta_3 - \sin\theta_2\sin\theta_3) \\ &=& x_r + L_2\cos\theta_1 - \sin\theta_1(L_3\cos\theta_2 + L_4\cos\theta_2\cos\theta_3 - L_4\sin\theta_2\sin\theta_3) \\ \end{eqnarray}$$

ここで、

$$A = L_3\cos\theta_2 + L_4\cos\theta_2\cos\theta_3 - L_4\sin\theta_2\sin\theta_3$$

と置いて、続きを計算してみます。

$$\begin{eqnarray} x_e &=& \cdots \\ &=& x_r + L_2\cos\theta_1 - A\sin\theta_1\\ &=& x_r - \sqrt{L_2^2 + A^2}\sin\left(\theta_1 - \tan^{-1}\frac{L_2}{A}\right) \end{eqnarray}$$

以上より、

$$\theta_1 = \sin^{-1}\left(-\frac{x_e - x_r}{\sqrt{L_2^2 + A^2}}\right) + \tan^{-1}\frac{L_2}{A}$$

となります。

さいごに

ここまで、運動学について順運動学と逆運動学の概要と、解法について説明してきました。また、具体例として、2自由度マニピュレータと3自由度マニピュレータの運動学についても示しました。

運動学を学ぶということについて、一般的に想像する学問を極めるような大変さを想像された方も多いかもしれませんが、扱う範囲は狭く、また取っ付きやすく、習得しやすい学問だと感じていただけたのではないかと思います。もちろん、極めようと思えば奥は深いので、簡単ではありません。

私自身、独学で学んだばかりで（また数学を忘れつつあったので…）、内容に誤りがあるかもしれません。
（間違いを見つけられた場合は、「お問い合わせフォーム」から一言お伝えしていただけると幸いです。）

とはいえ、本記事の内容を理解しておけば、3自由度マニピュレータの運動学のプログラムを自分で作成して、ロボットを動作させることが可能な内容となっているはずです。ぜひ、実践してみてください。

また、本記事の内容をベースとして、4脚ロボットの順運動学と逆運動学を導出する記事を執筆しました。併せてお読みいただけると幸いです。

【図解】4脚ロボットの順運動学と逆運動学

本記事では、4脚ロボットの運動学（順運動学と逆運動学）に焦点をあてて、一般的な4脚ロボットの歩行制御で利用可能な一般化された運動学の式を導出することを目標に解説していきます。 運動学（順運動学と逆運動 ...

最後までお読みいただきありがとうございました。