本記事では、4脚ロボットの運動学(順運動学と逆運動学)に焦点をあてて、一般的な4脚ロボットの歩行制御で利用可能な一般化された運動学の式を導出することを目標に解説していきます。
運動学(順運動学と逆運動学)について、概念的な内容と詳しい解法については、以前の記事↓で解説しているので、併せてお読みいただけると幸いです。
本記事の内容は動画でも解説していますので、ご活用ください。
運動学
運動学とは、ロボットの関節角度と位置や姿勢の関係を扱う分野で、各関節角度からロボットのエンドエフェクタの位置を導出するのが順運動学、エンドエフェクタの位置から各関節角度を導出するのが逆運動学です。
運動学の詳細については以下の記事で扱っているので、運動学の概要や順運動学や逆運動学の導出について知らない方は、ぜひ、以下の記事をお読みください。同次変換行列を用いた順運動学の導出など、本記事では解説せずに使用します。これらの詳細については下記の記事でご確認ください。例題を示しながら詳しく解説しています。
4脚ロボットの脚構造パターン
本記事のテーマの1つである、4脚ロボットの順運動学を考えるにあたり、4脚ロボットの脚の構造のパターンについて大まかに確認します。
まず、4脚ロボットというと、どのような形を思い浮かべますか?
実際に存在するロボットで言うと、Boston DynamicsのSpot、Unitree Go1やANYmalなどを思い浮かべる方が大半かもしれませんね。
マイナーかもしれませんが、Ghost RoboticsのMinitaurを想像された方もいるかもしれませんね。
Ghost RoboticsのMinitaurは例外としても、多くの方が想像した4脚ロボットの形状は、下図の2種類のうちどちらか一方に該当していると考えられます。

すなわち、4脚ロボットの大半は、左図のロボットのように前後の脚が互いに逆方向に曲がっているタイプ(ANYmal Cなど)と、右図のロボットのように同一方向に曲がっているタイプ(SpotやGo1など)のどちらか一方に該当すると考えられるのです。
説明の便宜上、左側をタイプA、右側をタイプBと呼ぶことにします。
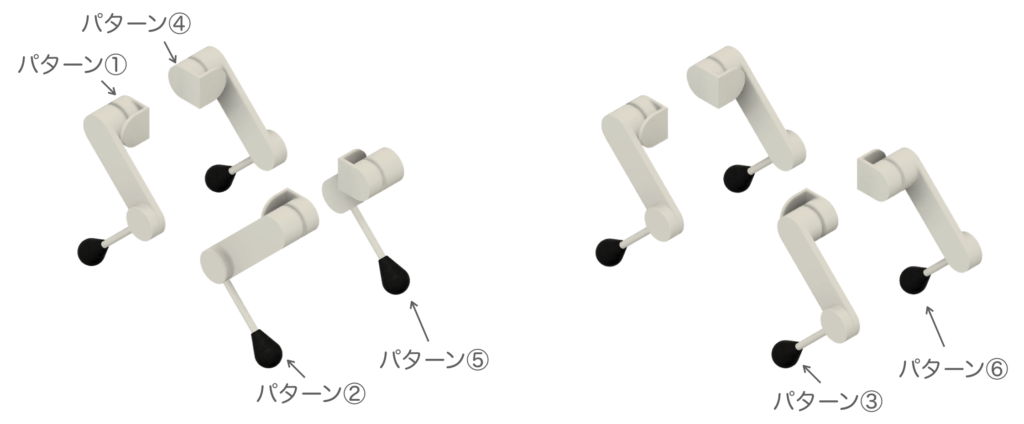
この記事では、タイプAとBの4脚ロボットで想定される脚構造を対象に運動学を導出することとします。では、この場合に想定される脚構造が何種類かをここで明らかにしておきます。以下の図では、先ほど紹介した2つのタイプのロボットの胴体を取り除き、脚だけを表示させたもので、8つの脚が記載されています。ここから重複している脚構造を取り除き、最低限考えておきたい脚構造を選定していきます。
まず、前提事項として、座標系をどのように配置するかにより、脚構造が重複するかしないかが異なるので、どの座標系を基準として運動学を導出するか決める必要があります。今回は、極力、4脚ロボットに限定して一般化されたものを導出したいので、4脚ロボットの胴体に座標系を置いて運動学を導出することにします。もう1つの座標系の置き方として、それぞれの脚の付け根付近に基準座標を置く考え方もあると思いますが、その場合、座標軸の正方向をどうするかなどを考える必要があると考えられるため採用しませんでした。
このように基準座標系を考えると、タイプAとタイプBの前脚構造のみ完全に重複します。よって、8つの脚構造から2つの重複分を差し引いた6種類が今回、考えていく脚構造となります。それぞれ、図のようにパターン①から⑥までナンバリングしました。
※基準座標系の違いによる重複する脚の違いについて補足します。もし、脚の付け根付近に基準座標系を置き、また、後脚の場合に限り基準座標系を鉛直軸に沿って180度回転させることを許すなら、タイプAの前左脚と後右脚、前右脚と後左脚も重複するものと考えることができます。ただし、私の直感ですが、使い勝手が悪そうな気がしたので採用しませんでした。
少し話がそれますが、近年は、さまざまな種類の4脚ロボットが登場していて、中には車輪付きのロボットまであります。それについて以前私が調べてまとめた記事があるので、興味がありましたら、開いて読んでみてください。
座標系の基礎知識
運動学を考えるに際し、どのような座標系で導出するのかを決めるのが重要だと先ほど説明しました。先ほどは、胴体に座標系を置くという程度の説明にとどめていましたが、ここでは、実装も考慮した具体的な話をしていきます。私は、Unityで4脚ロボットの運動学を扱う予定なので、Unityの座標系で解くことにしました。Unityは左手座標系です。ROSや一般的なCADソフトウェアは、右手座標系を採用しているので、同一に考えることができないのが欠点です。
左手座標系および右手座標系について説明します。左手座標系はUnityなどのCG系ソフトウェアでよく用いられ、\(y\)軸が上向きで\(z\)軸は奥行きを表します。右手座標系はROSやCADソフトなどハードウェア寄りのソフトウェアで用いられ、\(z\)軸が上向きです。また、回転の正方向が、左手座標系と右手座標系では逆になります。左手座標系の回転の正方向は左、右手座標系の回転の正方向は右です(右ネジ)。ここまで説明した内容を下図に示します。
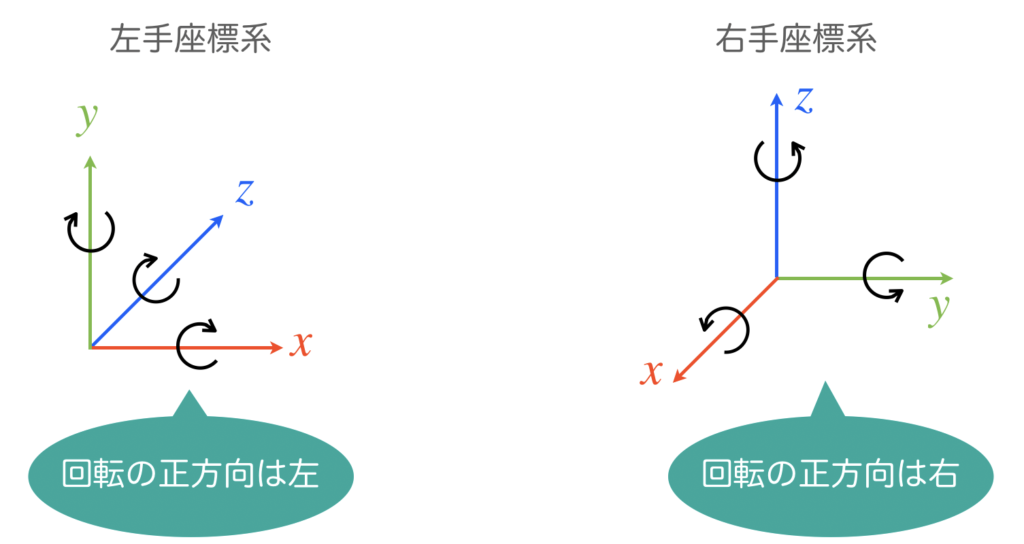
CG系は液晶ディスプレイなどの2次元画面にゲーム空間などを表示させることを前提とするため、ディスプレイを\(xy\)平面、奥行きを\(z\)とする左手座標系を採用していると考えられれます。
一方で、ROSやCADソフトでは、画面を通して見る点においてはCG系と同様ですが、どのように見えるかではなく、どのような物体が3次元空間に配置されているのか、設計されているのか、が重要となるため、地面を\(xy\)平面、高さを\(z\)とする右手座標系が採用されていると考えられます。
ロボットを設計するときに使用するCADソフトは一般的に右手座標系です(Fusion360など)。CADでロボットを設計する際は、\(x\)軸の正方向がロボットの前面となるように設計することをお勧めします。
\(x\)軸の正方向が前面となるように設計したロボットを、Unityに読み込むと、\(z\)軸の正方向が前面となるようにロードされます。
問題設定
座標系
今回は、Unityを用いるので、左手座標系を使用します。また、ロボットが移動しても問題なく扱いたいので、ロボットの胴体の重心付近に原点を持つローカル座標系を使用することとします。
ここで、ローカル座標系という概念について簡単に導入しておきます。まず、座標系は複数考えることができ、それらに親子関係を与えることができます。親子関係とは階層的であり、座標変化を階層構造として扱うことができるようになります。つまり、親の座標系の移動により子の座標系の絶対位置が変化したとしても親の座標系から見た子の座標系の位置は変化しないという便利な性質を扱えるようになります。
説明が難しいので具体例を挙げてみます。頭の中に、傘立てと傘の2つをイメージして下さい。今、傘立ての中には傘が入っていないとします。この状態で、傘立てと傘を1mだけ右に移動させたい場合、傘立てと傘の両方を1mだけ右に運ぶ必要があります。ここで、もし傘が傘立ての中に入っていたら、傘立てを移動させるだけで傘も移動します。傘を傘立てに入れる操作は、傘の座標系を傘立ての座標系の子にする操作と等価であり、傘の親の座標系が変化すれば、傘も変化すると言うことになります。つまり、物と物の繋がりや移動を階層的に扱えるのです。この考え方は、ロボットのように複数のリンクと関節を持つ機構を扱うのに大変便利です。
もし座標系の親子関係を用いな場合、ロボットの動作をシミュレータの最上位の座標系(=絶対座標系)で全て定義する必要がありますが、親子関係を用いれば、ロボットの胴体の重心付近にある座標系(絶対座標系の子の座標系)を基準に、その範囲内で考えれば良いため、ロボットの移動が脚の位置などの計算に影響を与えなくなり、とても扱いやすくなります。
Unityでは親子関係のある座標系を扱うことができ、親の座標系を持たない最上位の座標系(シーンの中心)をワールド座標系、親の座標系を持つ座標系をローカル座標系と呼びます。ワールド座標系は1つしかないですが、ローカル座標系は複数考えることができます。
話が長くなりましたが、4脚ロボットの胴体の重心付近を原点とするローカル座標系を用いて運動学を計算することにします。この座標系をロボットに書き込んでみました(下図)。

デフォルト状態
次に、ロボットのデフォルト状態(全ての関節角度を0とした状態)を規定する必要があります。これを決めないと関節角度を与えることができません。そこで、デフォルト状態を下図の通りとします。すなわち、4つの脚が鉛直下方向に関節を曲げることなくまっすぐ伸ばした状態です。

豆知識ですが、4脚ロボットを設計する際は、下図のように足を伸ばした状態で設計することをお勧めします。
回転の正方向
次に、各関節の回転の正方向を決めます。これを規定しておかないと、様々な4脚ロボットに対応可能な一般化された制御器を作ることができません。
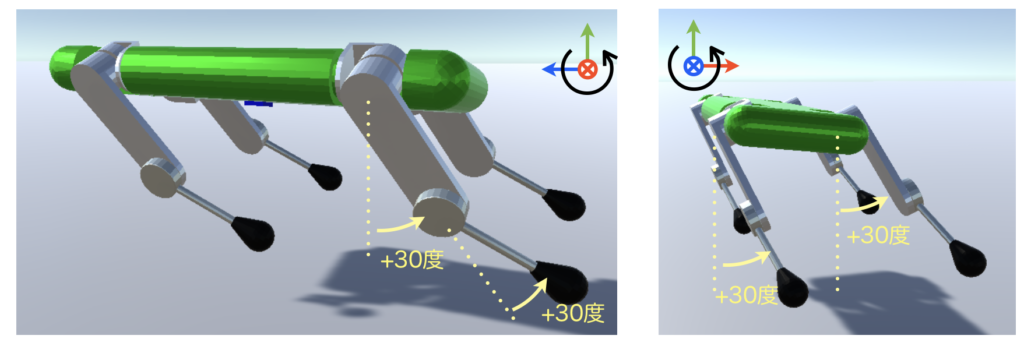
そこで、それぞれの関節の回転の正方向を該当の座標系の軸における回転の正方向と一致させることにします。このとき、すべての関節の角度を30度に設定すると以下のようなポーズとなります。
各種パラメータ
今回の問題設定において使用するパラメータを、
- 付け根の位置ベクトル
- エンドエフェクタ位置
- 各リンクの長さ
- 回転角
の4種類とします。
付け根の位置ベクトル
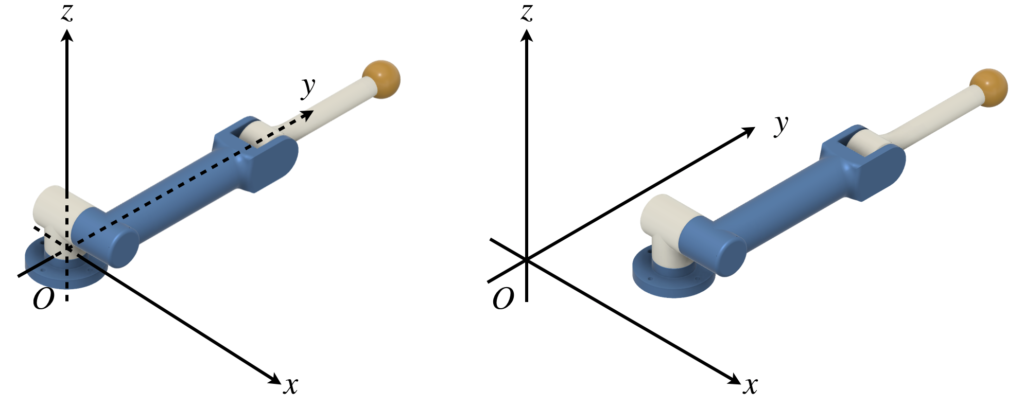
脚をマニピュレータとして考えてみます。マニピュレータの順運動学を求めるとき、マニピュレータの付け根の関節に座標系をおくことが一般的です(下図左)。しかし、今回扱いたい問題において、基準とする座標系の原点は、胴体の重心付近であり、マニピュレータの付け根部分の関節ではありません(下図右)。そのため、座標系の原点からマニピュレータの付け根の関節までの位置ベクトルを考慮した計算式を導出する必要があります。
以下の記事では、上記右の問題設定で運動学を導く方法と結果を紹介しています。4脚ロボットの脚の運動学を解く方法と全く同じです。
上の記事では、4脚ロボットに限定しない一般的な問題として解いているので、興味がありましたら上の記事を参考にしてみて下さい。
4脚ロボットの胴体にある基準座標系において、それぞれのマニピュレータの付け根の関節までのベクトルを
$$\begin{pmatrix}
x_r\\y_r\\z_r
\end{pmatrix}$$
とします。下付き文字の\(r\)は、rootのrです。このベクトルは、どれか1種類の脚の付け根の関節位置を表す固定ベクトルものというよりは、指定された脚の運動学を求める関数の仮引数だと考えてください。
エンドエフェクタ位置
胴体の基準座標系から見たエンドエフェクタの位置ベクトルを
$$\begin{pmatrix}
x_e\\y_e\\z_e
\end{pmatrix}$$
と定義します。
各リンクの長さ
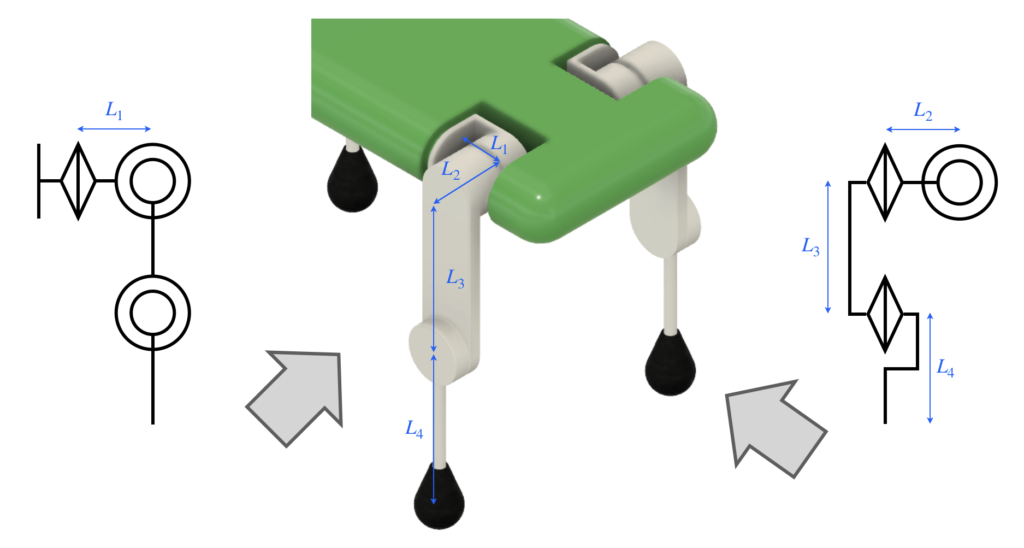
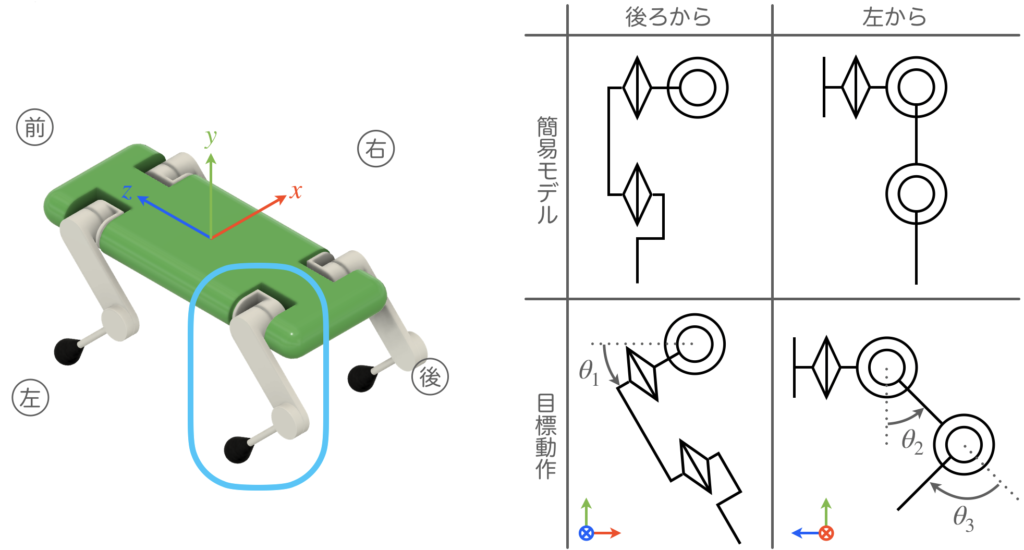
扱う脚を単純な構造でモデル化します。下図(中)の4脚ロボット脚を、矢印の2方向からみると、それぞれ左図と右図に示すような簡易的な機構でモデル化できます。左図と右図は、投影した方向が異なるだけで、両者は同じく脚を表しており、3つのリンクと3つの関節からなります。ただし、付け根部分から肩にかけてのリンクはL字形を想定しているため、長さのパラメータとしては、\(L_1~L_4\)の4つとなります。
回転角
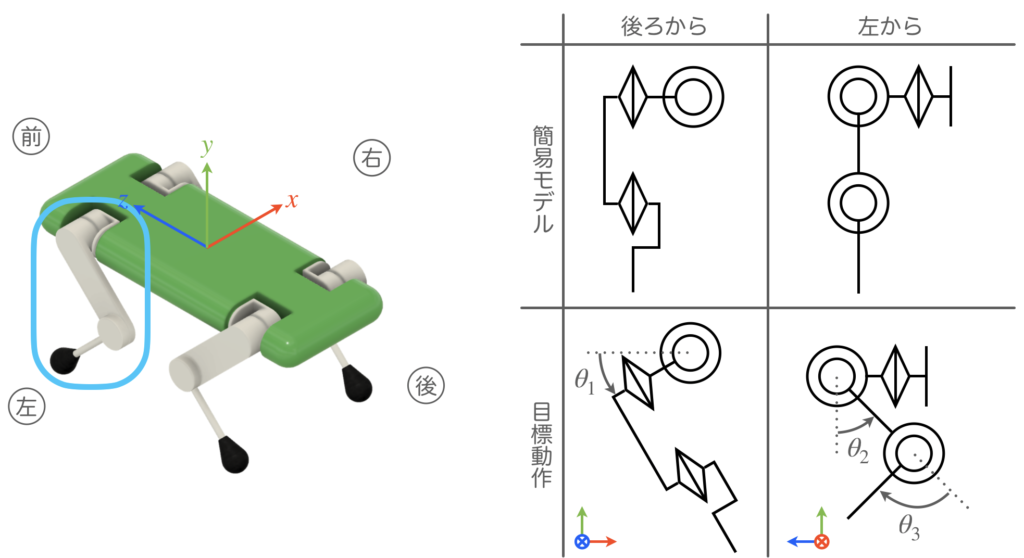
3つの関節の回転角を、付け根部分から順番に、\(\theta_1\)、\(\theta_2\)、\(\theta_3\)とします。これらの角度信号が入力されたときに、どのような脚の形状に変化するかをそれぞれ規定し、そのときの順運動学を6つ導出します。そして、それらが一つのソルバから全て同一視できるように符号関数を導入し、6種類の脚の順運動学の式を一般化します。
4脚ロボットの順運動学
先ほど示した6つの脚パターンについて、同次変換行列を用いて順運動学を導出し、最後に一般化します。
パターン①
$$\begin{eqnarray}
\begin{pmatrix}
x_e \\y_e \\z_e \\1
\end{pmatrix}&=&\begin{pmatrix}
\cos\theta_1 & -\sin\theta_1 & 0 & x_r \\
\sin\theta_1 & \cos\theta_1 & 0 & y_r \\
0 & 0 & 1 & z_r \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & -L_2 \\
0 & \cos\theta_2 & -\sin\theta_2 & 0 \\
0 & \sin\theta_2 & \cos\theta_2 & L_1 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta_3 & -\sin\theta_3 & -L_3 \\
0 & \sin\theta_3 & \cos\theta_3 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\-L_4 \\0 \\1
\end{pmatrix}
\end{eqnarray}$$
$$\left\{
\begin{array}{ccl}
x_e &=& L_4\sin\theta_1\cos(\theta_2 - \theta_3) + L_3\sin\theta_1\cos\theta_2 - L_2\cos\theta_1 + x_r \\
y_e &=& -L_4\cos\theta_1\cos(\theta_2 - \theta_3) - L_3\cos\theta_1\cos\theta_2 - L_2\sin\theta_1 + y_r \\
z_e &=& -L_4\sin(\theta_2 - \theta_3) - L_3\sin\theta_2 + L_1 + z_r
\end{array}
\right.$$
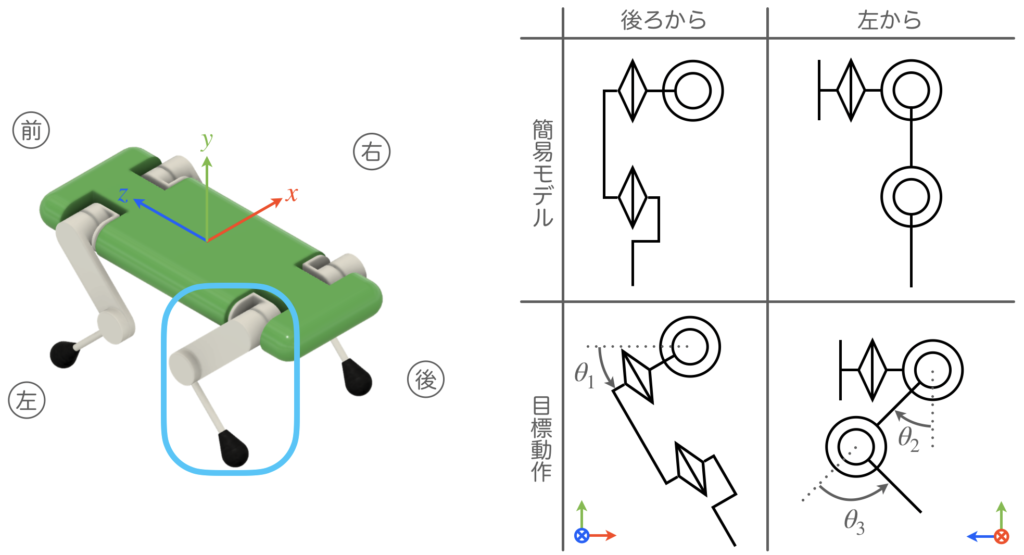
パターン②
$$\begin{eqnarray}
\begin{pmatrix}
x_e \\y_e \\z_e \\1
\end{pmatrix}&=&\begin{pmatrix}
\cos\theta_1 & -\sin\theta_1 & 0 & x_r \\
\sin\theta_1 & \cos\theta_1 & 0 & y_r \\
0 & 0 & 1 & z_r \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & -L_2 \\
0 & \cos\theta_2 & \sin\theta_2 & 0 \\
0 & -\sin\theta_2 & \cos\theta_2 & -L_1 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta_3 & -\sin\theta_3 & -L_3 \\
0 & \sin\theta_3 & \cos\theta_3 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\-L_4 \\0 \\1
\end{pmatrix}
\end{eqnarray}$$
$$\left\{
\begin{array}{ccl}
x_e &=& L_4\sin\theta_1\cos(\theta_2 - \theta_3) + L_3\sin\theta_1\cos\theta_2 - L_2\cos\theta_1 + x_r \\
y_e &=& -L_4\cos\theta_1\cos(\theta_2 - \theta_3) - L_3\cos\theta_1\cos\theta_2 - L_2\sin\theta_1 + y_r \\
z_e &=& L_4\sin(\theta_2 - \theta_3) + L_3\sin\theta_2 - L_1 + z_r
\end{array}
\right.$$
パターン③
$$\begin{eqnarray}
\begin{pmatrix}
x_e \\y_e \\z_e \\1
\end{pmatrix}&=&\begin{pmatrix}
\cos\theta_1 & -\sin\theta_1 & 0 & x_r \\
\sin\theta_1 & \cos\theta_1 & 0 & y_r \\
0 & 0 & 1 & z_r \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & -L_2 \\
0 & \cos\theta_2 & -\sin\theta_2 & 0 \\
0 & \sin\theta_2 & \cos\theta_2 & -L_1 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta_3 & \sin\theta_3 & -L_3 \\
0 & -\sin\theta_3 & \cos\theta_3 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\-L_4 \\0 \\1
\end{pmatrix}
\end{eqnarray}$$
$$\left\{
\begin{array}{ccl}
x_e &=& L_4\sin\theta_1\cos(\theta_2 - \theta_3) + L_3\sin\theta_1\cos\theta_2 - L_2\cos\theta_1 + x_r \\
y_e &=& -L_4\cos\theta_1\cos(\theta_2 - \theta_3) - L_3\cos\theta_1\cos\theta_2 - L_2\sin\theta_1 + y_r \\
z_e &=& -L_4\sin(\theta_2 - \theta_3) - L_3\sin\theta_2 - L_1 + z_r
\end{array}
\right.$$
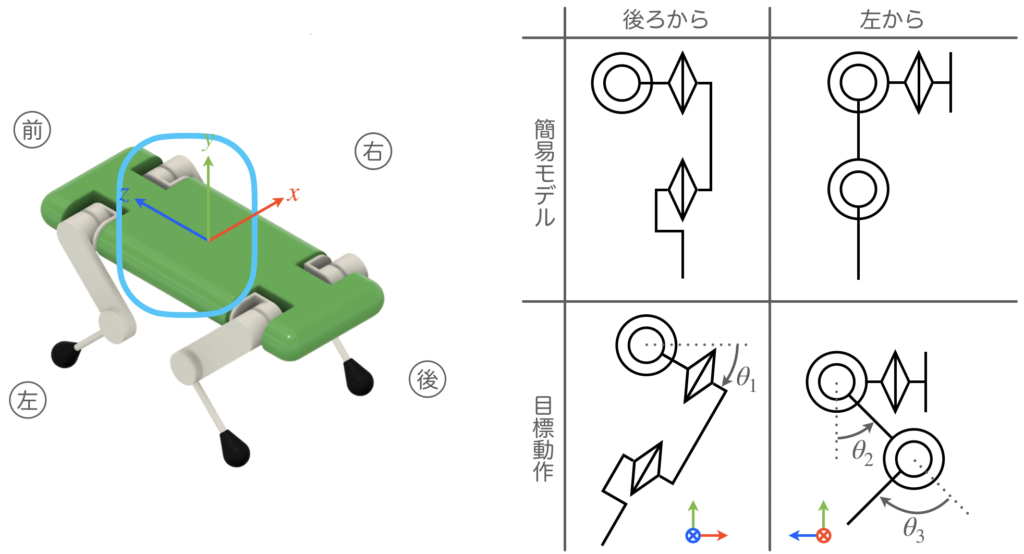
パターン④
$$\begin{eqnarray}
\begin{pmatrix}
x_e \\y_e \\z_e \\1
\end{pmatrix}&=&\begin{pmatrix}
\cos\theta_1 & \sin\theta_1 & 0 & x_r \\
-\sin\theta_1 & \cos\theta_1 & 0 & y_r \\
0 & 0 & 1 & z_r \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & L_2 \\
0 & \cos\theta_2 & -\sin\theta_2 & 0 \\
0 & \sin\theta_2 & \cos\theta_2 & L_1 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta_3 & \sin\theta_3 & -L_3 \\
0 & -\sin\theta_3 & \cos\theta_3 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\-L_4 \\0 \\1
\end{pmatrix}
\end{eqnarray}$$
$$\left\{
\begin{array}{ccl}
x_e &=& -L_4\sin\theta_1\cos(\theta_2 - \theta_3) - L_3\sin\theta_1\cos\theta_2 + L_2\cos\theta_1 + x_r \\
y_e &=& -L_4\cos\theta_1\cos(\theta_2 - \theta_3) - L_3\cos\theta_1\cos\theta_2 - L_2\sin\theta_1 + y_r \\
z_e &=& -L_4\sin(\theta_2 - \theta_3) - L_3\sin\theta_2 + L_1 + z_r
\end{array}
\right.$$
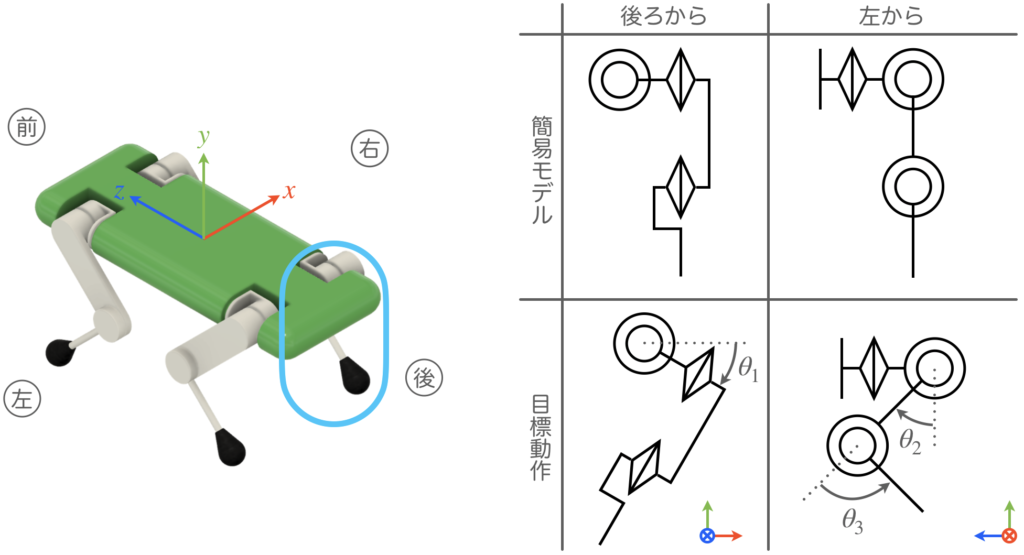
パターン⑤
$$\begin{eqnarray}
\begin{pmatrix}
x_e \\y_e \\z_e \\1
\end{pmatrix}&=&\begin{pmatrix}
\cos\theta_1 & \sin\theta_1 & 0 & x_r \\
-\sin\theta_1 & \cos\theta_1 & 0 & y_r \\
0 & 0 & 1 & z_r \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & L_2 \\
0 & \cos\theta_2 & \sin\theta_2 & 0 \\
0 & -\sin\theta_2 & \cos\theta_2 & -L_1 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta_3 & -\sin\theta_3 & -L_3 \\
0 & \sin\theta_3 & \cos\theta_3 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\-L_4 \\0 \\1
\end{pmatrix}
\end{eqnarray}$$
$$\left\{
\begin{array}{ccl}
x_e &=& -L_4\sin\theta_1\cos(\theta_2 - \theta_3) - L_3\sin\theta_1\cos\theta_2 + L_2\cos\theta_1 + x_r \\
y_e &=& -L_4\cos\theta_1\cos(\theta_2 - \theta_3) - L_3\cos\theta_1\cos\theta_2 - L_2\sin\theta_1 + y_r \\
z_e &=& L_4\sin(\theta_2 - \theta_3) + L_3\sin\theta_2 - L_1 + z_r
\end{array}
\right.$$
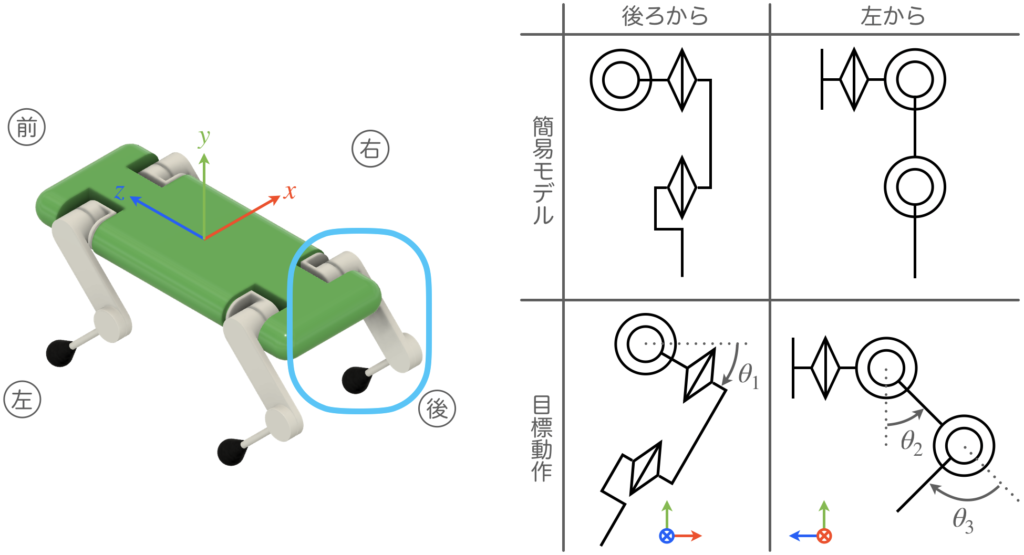
パターン⑥
$$\begin{eqnarray}
\begin{pmatrix}
x_e \\y_e \\z_e \\1
\end{pmatrix}&=&\begin{pmatrix}
\cos\theta_1 & \sin\theta_1 & 0 & x_r \\
-\sin\theta_1 & \cos\theta_1 & 0 & y_r \\
0 & 0 & 1 & z_r \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & L_2 \\
0 & \cos\theta_2 & -\sin\theta_2 & 0 \\
0 & \sin\theta_2 & \cos\theta_2 & -L_1 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta_3 & \sin\theta_3 & -L_3 \\
0 & -\sin\theta_3 & \cos\theta_3 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\-L_4 \\0 \\1
\end{pmatrix}
\end{eqnarray}$$
$$\left\{
\begin{array}{ccl}
x_e &=& -L_4\sin\theta_1\cos(\theta_2 - \theta_3) - L_3\sin\theta_1\cos\theta_2 + L_2\cos\theta_1 + x_r \\
y_e &=& -L_4\cos\theta_1\cos(\theta_2 - \theta_3) - L_3\cos\theta_1\cos\theta_2 - L_2\sin\theta_1 + y_r \\
z_e &=& -L_4\sin(\theta_2 - \theta_3) - L_3\sin\theta_2 - L_1 + z_r
\end{array}
\right.$$
一般化
上で示した6つのパターンについて、コントローラから全く同じ状態として扱いたいので、適切な係数を設定して1つの式にまとめました。以下に結果を示します。
式を比較すると、左右どちらの脚か、前後どちらの脚か、ロボットのタイプはどちらかの3種類について符号関数を用意することで、1つの式にまとめることができました。使用した3つの符号関数は以下の通りです。
$$sign_{lr} = \left\{
\begin{array}{lr}
1&\mbox{(left leg)}\\
-1&\mbox{(right leg)}
\end{array}
\right.$$
$$sign_{type} = \left\{
\begin{array}{lr}
1&\mbox{(type B, Type A and B)}\\
-1&\mbox{(type A)}
\end{array}
\right.$$
$$sign_{fb} = \left\{
\begin{array}{lr}
1&\mbox{(forward leg)}\\
-1&\mbox{(back leg)}
\end{array}
\right.$$
このとき、
$$\left\{
\begin{array}{ccl}
x_e &=& sign_{lr} × L_4\sin\theta_1\cos(\theta_2 - \theta_3) + sign_{lr} × L_3\sin\theta_1\cos\theta_2 - sign_{lr} × L_2\cos\theta_1 + x_r \\
y_e &=& -L_4\cos\theta_1\cos(\theta_2 - \theta_3) - L_3\cos\theta_1\cos\theta_2 - L_2\sin\theta_1 + y_r \\
z_e &=& -sign_{type} × L_4\sin(\theta_2 - \theta_3) - sign_{type} × L_3\sin\theta_2 + sign_{fb} × L_1 + z_r
\end{array}
\right.$$
と表すことができます。
4脚ロボットの逆運動学
上で求めた順運動学の式から逆運動学を導出します。導出手順は、以下の記事における3自由度マニピュレータの逆運動学の導出と全く同じなので、途中は省略し、結果のみ示します。
導出結果は以下のようになります。
$$
\theta_3 = - sign_{type}×cos^{-1}\left(\frac{(x_e - x_r)^2 + (y_e-y_r)^2 + (z_e - z_r - sign_{fb}×L_1)^2 - L_2^2 - L_3^2 - L_4^2}{2L_3L_4}\right)
$$
$$
\theta_2 = - sign_{type}×sin^{-1}\left(\frac{z_e - z_r - sign_{fb}×L_1}{-sign_{type}×\sqrt{(x_e - x_r)^2 + (y_e-y_r)^2 + (z_e - z_r - sign_{fb}×L_1)^2 - L_2^2}}\right) - tan^{-1}\left(\frac{L_4\sin\theta_3}{L_3 + L_4\cos\theta_3}\right)
$$
$$
\theta_1 = sign_{lr}×\left\{sin^{-1}\left(\frac{x_e - x_r}{sign_{lr}\sqrt{L_2^2 + A^2}}\right)+\tan^{-1}\frac{L_2}{A}\right\}
$$
ただし、
$$
A = L_3\cos\theta_2 + L_4\cos\theta_2\cos\theta_3 - L_4\sin\theta_2\sin\theta_3
$$
さいごに
本記事では、順運動学と逆運動学の応用先として、4脚ロボットの例をあげて説明しました。
Unityでプログラムを作成し、Unitree Go1の仮想モデルを歩かせてみたところ、全く問題なく自然に歩行できたので、上記の導出結果は間違っていないと考えられますが、改善すべき点は多く残っているので、追々、考えていけたらと思っています。
最後までお読みいただき、ありがとうございました。