当記事では数式を使わずに、LSTMとGRUのエッセンスを直感で理解できるように説明します。同様の説明をYouTube動画にアップしているのでぜひご活用ください!
当サイトはTwitterやYouTubeでも情報発信しています。ご気軽にフォロー(@AGIRobots)、チャンネル登録お願いします!
少し新しい情報を追加したリメイク動画も公開しています!⇓
これだけは(ポイント)
本記事で話す内容の中で、重要な部分をピックアップして箇条書きにしました。
ポイント
RNN: 再帰構造により系列データを学習可能にするニューラルネットワークの総称。最も単純なRNNには、勾配消失問題と重み衝突という二つの理由により長期的な特徴の学習は苦手であるため、内部に記憶素子やゲート機構(Attentionに似た仕組み)を取り入れたLSTMやGRUなどが提案された。
LSTM: 長期的特徴と短期的特徴を学習することができる。欠点は計算量が多いこと。
GRU: LSTMの代替となるモデルでLSTMより計算量が少なくてすむ。性能はLSTMと変わらないとされている。
順伝播型ニューラルネットワーク(FNN)
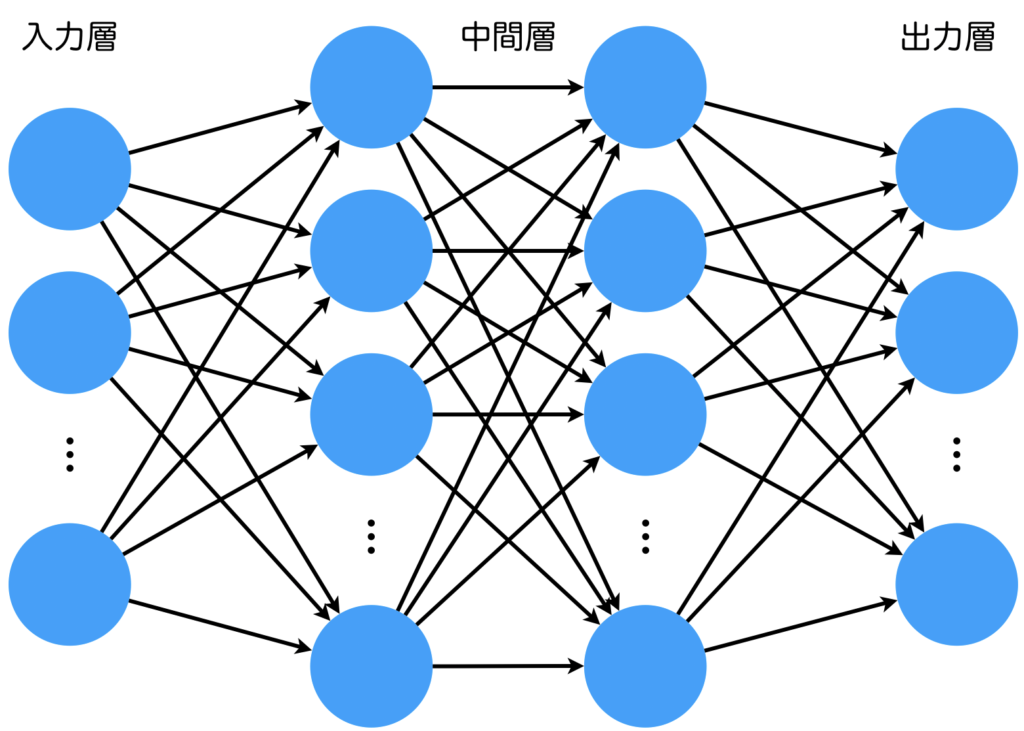
順伝播型ニューラルネットワーク(Feedforward Neural Network: FNN)とは、生体の神経細胞を数理的にモデル化し、何層もスタックしたニューラルネットワークのことです。最も単純な順伝播型ニューラルネットワークは、入力層、中間層、出力層の3層構造からなります。最近では中間層の数を2層以上にした深層ニューラルネットワーク(Deep Neural Network: DNN)が主流となってきています。ニューラルネットワークは古くから研究されていましたが、学習の難しさや、計算機のマシンパワー不足など、さまざまな理由が重なり、2010年頃まではあまり注目されませんでした。しかし、現在は、大規模なデータセット、高性能な計算機などが存在し、深層ニューラルネットワークを使った技術が驚くような性能を達成しています。学習では誤差逆伝播(Backpropagation: BP)を用いるのが一般的です。誤差逆伝播については以下の記事で詳しく説明しています。
再帰型ニューラルネットワーク(RNN)の基礎
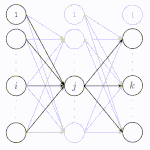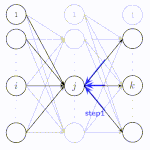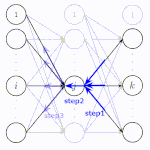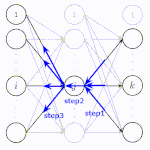
再帰型ニューラルネットワーク(Recurrent Neural Network: RNN)とは、順伝播型ニューラルネットワークの中間層に再帰的な構造を持たせたニューラルネットワークの総称です。矢印の終始が同じニューロンとなっている部分が再帰です。このニューロンのことを再帰セルと呼びます。再帰的な構造は過去の情報を未来の結果に伝播することを可能にするため、時系列処理において大きな成果を出しました。系列処理には、音声信号処理、言語処理などがあり、今でも基本的な技術はRNNに基づいているものがあります。RNNの学習では通時的誤差逆伝播(Backpropagation Through Time: BPTT)が用いられます。しかし、BPTTでは長期的特徴を学習することは苦手という問題があります。
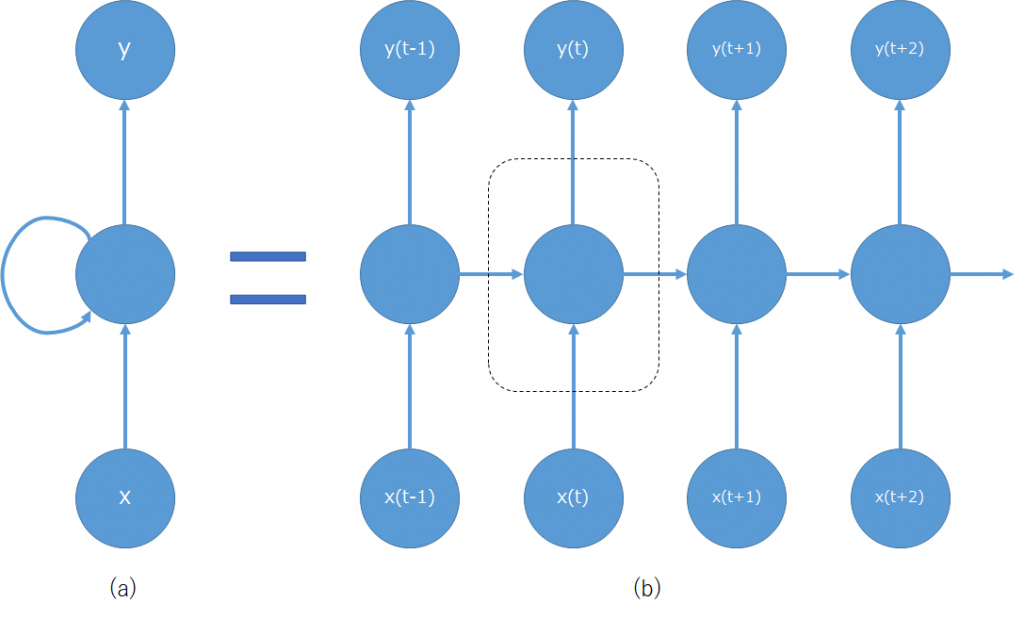
再帰型ニューラルネットワークには(a)のように時間軸上に展開されていない
(ノード間を通る情報がどの時刻のものか理解しにくい)表記と、
(b)のように時間軸上に展開されている表記の2種類がある。
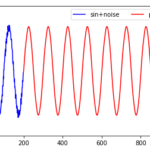
RNNで系列データを学習させてみたい場合は、以下の記事をご参考ください。以下の記事では正弦波を学習させています。
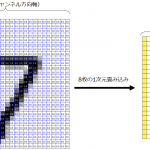
少し知識がある方だと系列情報はFNNでも扱えるのではないか?という疑問を持つかもしれません。その答えはYesです。入力データの形式を工夫することで可能になります。RNNでは内部の再帰構造により系列処理を可能にしているので、入力データは現在の時刻のデータのみですが、FNNは内部に記憶構造を持たないため、現在の入力と過去の入力を合体させてFNNに入力してあげる必要があります(工夫することで減らすことはできます)。
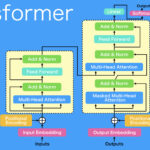
過去の情報を含めて入力するニューラルネットワークに1次元畳み込みや近年驚異的な知能を発揮しているTransformerがあります。興味がありましたら、以下のリンクの記事をお読みいただければと思います。
RNNの表記
先ほど示したRNNの図において注目してほしいのは、RNNの表記には2種類あることです。違いは時間軸での展開の有無です。(a)は時間軸で展開していません。(b)は時間軸で展開しています。単純なRNNなら(a)の表記でも問題ないですが、LSTMなど複雑な再帰セルを持つRNNの場合、再帰セルの内部を詳しく説明する図が多く登場してきますが、時間軸で展開しているかどうかで記される表が大きく変わりますので、しばしば初心者を混乱させる要因となっています。この点は十分に理解しておきましょう。
RNNの学習の難しさ
先ほど、RNNは長期的特徴を学習することは苦手ということを一瞬だけ触れました。ここでは、その要因である勾配消失問題と重み衝突の2つが関与しています。
勾配消失問題
勾配消失問題とは、FNNで誤差逆伝播を用いて重みを更新するとき、入力層側へ伝播していく際に勾配が消失してしまい、重みが更新されなくなってしまう現象です。こうなると、深層にしても学習しているのは出力層側の数層のみということになり、精度は上がらず計算コストは高いという最悪な状態になります。勾配消失の原因に、当時使用されていた活性化関数であるシグモイド関数(sigmoid)やハイパボリックタンジェント(tanh)の微分値が1より小さいことが挙げらました。多層になればなるほど、活性化関数の微分値を繰り返し乗算する回数が増えるため、どんどん伝播される値が小さくなってしまいます。
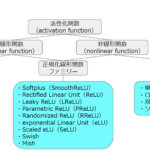
そこで、誤差逆伝播に向いているさまざまな活性化関数が登場しました。現在では、ランプ関数(Rectified Linear Unit: ReLU)が使用されることが多いです。さまざまな活性化関数に興味がある方は以下の記事をご参考ください。
FNNではニューラルネットワークを深層にすることで勾配消失問題が発生しましたが、RNNは再帰セルでループ構造を成すため、時間軸で展開すれば分かるとおりFNNで発生した勾配消失問題が時間軸方向に対しても発生します。すなわち、遠い過去の情報に対しては学習されないのです。では、FNNと同様に活性化関数を工夫すれば良いのかというと、そう単純な問題ではないことがわかります。それを理解するには次に説明する重み衝突問題について知る必要があります。そのため、FNNとは全く異なる方法で勾配消失に対処しました。
重み衝突
RNNでは系列データを扱います。系列データは、ある時刻のデータ単体ではなく系列であることで意味を成します。しかし、RNNは、1時刻ずつデータを処理します。それゆえ、重みの決定が難しいのです。説明が難しいですが、ある時刻における再帰セルへの入力に対して重みを決定するとき、現時点では重要性が低そうだということで重みを小さくしたくても、未来では重要だったので大きくしたいとなると、どちらに調節したら良いでしょうか?これが重み衝突です。
重み衝突は、再帰セルの入力側の重みと出力側の重みに対して考えることができ、それぞれ入力重み衝突と出力重み衝突と呼びます。
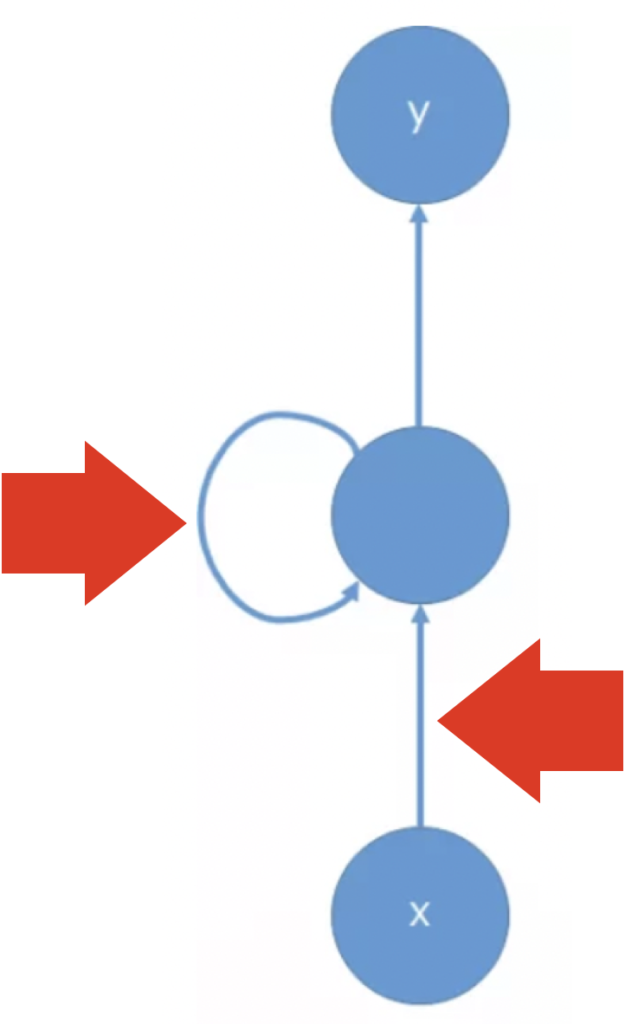
- 入力重み衝突とは、「現在の入力の重みを調節するとき、有用なら重みを大きく、無用なら重みを小さくしたいが、有用か無用かは将来になってみないと分からないため、有用として扱うことも無用として扱うこともできなず、重みを適切に設定することができない」という問題です。
- 出力重み衝突とは、「現時刻の出力の重みを調節するとき、有用なら重みを大きく、無用なら重みを小さくしたいが、有用か無用かは将来になってみないと分からないため、有用として扱うことも無用として扱うこともできなず、重みを適切に設定することができない」という問題です。
再帰セルに入力された入力層および再帰セルから信号が、長期的な特徴をもつのか短期的な特徴を持つのか分からない状態において、重みを大きくすべきか小さくすべきか決定できない問題を重み衝突といいます。RNNの再帰セルは単純なニューロンモデルが使用されるため、現在の入力が有用かどうかのみを判定することになり、必然的に短期的な記憶は学習できますが、長期的な記憶は学習することがきません。
以上の理由から、RNNではLSTMやGRUに代表されるような、記憶構造を持つ複雑なセルが考えられました。
LSTM
RNNの問題の対処
RNNが長期的な特徴を学習できない理由として、勾配消失問題と重み衝突の2つを説明しました。LSTMでは両問題を以下の方法で対処します。
- 勾配消失問題
→誤差を保存するセル(Constant Error Carrousel:CEC)を使用する(記憶セルを用意)。 - 重み衝突(入力重み衝突・出力重み衝突)
→入力ゲート・出力ゲートを使用する
CECセルについては、勾配消失問題により長期にわたる誤差逆伝播が不可能(すなわち、長期にわたる記憶が不可能)ならば、専用の記憶セルを用意して長期的な記憶が可能なアーキテクチャにすれば良いというアイディアです。
ゲート機構については、重み衝突に関して入力層から再帰セルに入力される信号や再帰セルから再帰セルに入力される信号を適切に処理(どの程度と通すか)するゲートを用意することで対処するというアイディアです。ゲート機構については、Transformerでも使用されているAttentionに近い構造ですね。
付随して必要になる仕組み
上で述べた対処法には2つの問題点が付随して生じます。
1つ目は記憶セルに記憶された情報をどのようにリセットするかです。リセットする仕組みがないと、永遠に入力ゲートからの入力が加算されることになり、過去の記憶が将来の判断に影響を及ぼす可能性があります。そこで、忘却ゲートをという忘れさせる仕組みを用意します。これにより、CECセルに記憶された情報を適切に忘却することができます。
2つ目はそれぞれのゲートをどのように操作するかです。入力信号の通過具合を調節する入力ゲート、再帰セルの出力信号の通過の程度を調節する出力ゲート、どの程度情報を忘却するか調節する忘却ゲートは神様ではないので、いつどのように処理すべきか学習しなければ分かりません。そこで、それぞれのゲートを操作するゲートコントローラ、すなわち新たなニューロンを用意します。ゲートでは乗算のみで通過する情報量を調節できるように、ゲートコントローラのニューロンは0~1を出力するように設定します。そのため、活性化関数としてシグモイド関数が使用されることが一般的となります。
Basic LSTM
ここでは、LSTMの中でも最も基本的な、Basic LSTMについて説明します。Basic LSTMの構成要素は以下の4つです。
- 記憶セル(CECセル)
- 入力ゲート・出力ゲート・忘却ゲート
- ゲートを操作するニューロン(3つ)
- セルへの入力を求めるニューロン(1つ)
Basic LSTMは、セルへの入力を求めるニューロンが1つ、CECセルを操作するゲートコントローラニューロンが3つの合計4つのニューロンで実現されていると解釈できます。それでは、時間軸で展開した基本LSTMセルの表記と時間軸で展開していない表記を見てみます。
時間軸展開していない表記
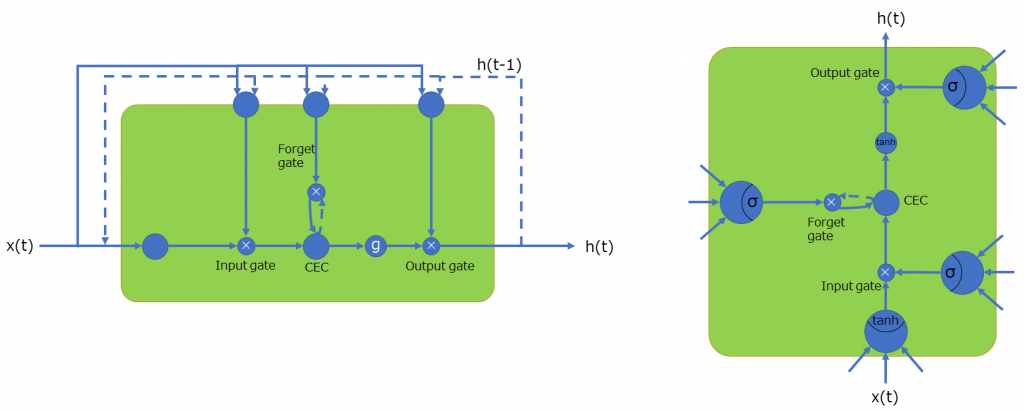
時間軸で状態を展開しない場合の表記を2つ示してみました。前時刻の情報は点線で示しています。左側の表記は入門書等で頻繁に見かける図ですね。また、右のような図もしばしば見かけます。主な違いは、どこがニューロンか一目で判断できることと、向きが横ではなく縦である点です。
左図の上に位置する3つのニューロンが入力ゲート・忘却ゲート・出力ゲートを操作するゲートコントローラです。ゲートはゲートコントローラからの出力値(0~1)を乗算します。\(g\)は活性化関数を表し、デフォルト値としてtanhが使用されることが多いです。また、gは省略されることがあります。
時間軸展開した表記
時間軸展開しない表記には、CECと\(h\)(もしくは出力\(y\))の2つが時間を扱う状態ベクトルであることが分かります。すなわち、この二つを時間軸上に展開して図を描けばいいのです。すると、以下の図になります。
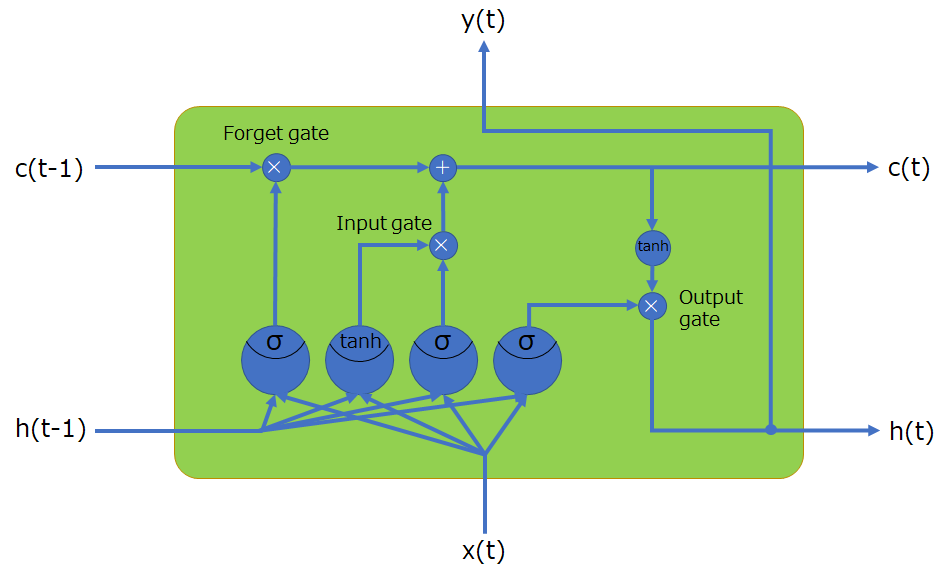
覗き穴結合(ピープホール結合)
実は、ここまでで説明してきたBasic LSTMはあまり使用されません。我々がLSTMというときに使用されるセルはこれから説明する覗き穴結合(ピープホール結合)という接続が内部的に存在します。
Basic LSTMの問題点:CECの気持ちが無視されている
ゲートコントローラは入力\(x(t)\)と直前の出力\(h(t-1)\)のみを判断材料として、全結合計算をするため、CECの記憶の忘却、更新や出力などに、CECセルが保持している長期記憶情報が考慮されません。
改善策:CECに耳を傾けてあげよう
改善策は簡単です。CECに耳を傾けられるように、ゲートコントローラと接続を作ればよいのです。具体的には、入力ゲートと忘却ゲートを操作するニューロンには時刻\(t-1\)の値が、出力ゲートを操作するニューロンには時刻\(t\)の値が届くように接続します。
一般的なLSTM
それでは、Basic LSTMに覗き穴結合(ピープホール結合)を加えた場合のLSTMセルの構造を先ほどと同様に時間軸で展開していない表記と展開した表記について見てみます。
時間軸展開していない表記
基本LSTMセルのモデルで示した図において、新たに3つ接続が増えていることが分かります。
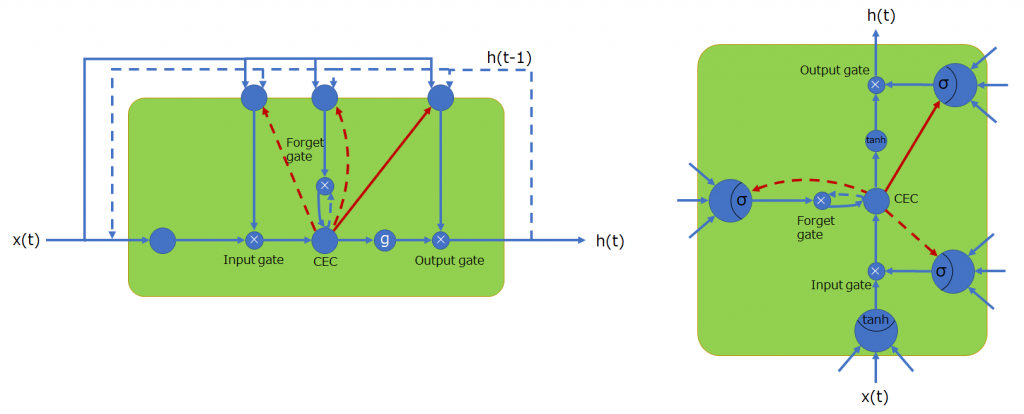
少し言及しましたが、出力ゲートのゲートコントローラには過去の状態ではなく、現在の状態が反映されるよう、現在の値が覗ける接続になっています。
時間軸展開した表記
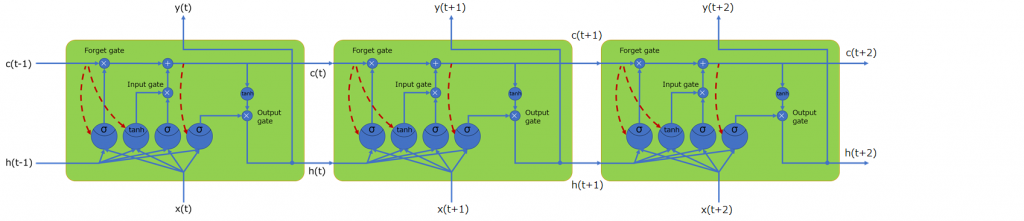
これも同様で、Basic LSTMセルモデルに、3つの覗き穴結合が追加されただけです。
※以下の図において、ピープホール結合を表す矢印が一か所間違っていました。tanhを活性化関数に持つニューロンではなく、その右のニューロン(入力ゲートコントローラ)へ矢印を引くのが正解です。
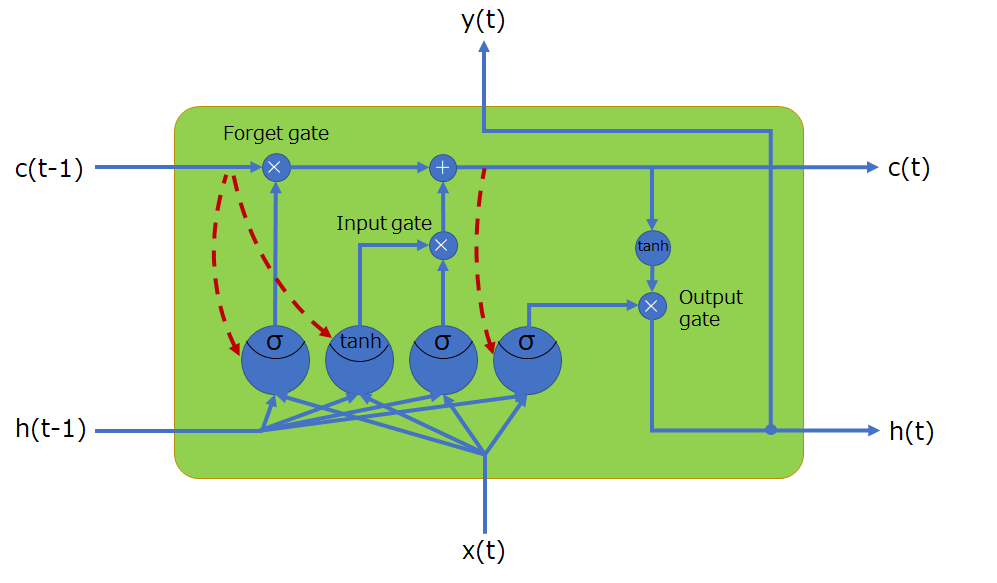
時間軸方向にセルを並べてみると、以下のような感じになります。
GRU
それでは、GRUについて説明します。GRU(Gated Recurrent Unit)セルは、LSTMと同様の性能を持つとされており、LSTMより計算量が少なく、高速に学習を進めることができます。
LSTMの欠点
LSTMはRNNで不可能だった長期的特徴の学習を可能にしたセルですが、計算コストが大きいという問題点があります。計算コストが大きいことは、機械学習に限らず好ましくありません。
アイディア
解決策として、状態ベクトル数を減らす、ゲートコントローラ数を減らすという主に2つのアプローチで改善策を考えていきます。
- 状態ベクトル数を減らす(時間依存の状態数を減らす)
LSTMではCECと\(h\)の2つが状態を保持していました。これを1つにまとめます。
これにより、記憶セルという構造は無くなります。 - ゲートコントローラ数を減らす
LSTMでは入力ゲート、忘却ゲート、出力ゲートに1つずつゲートコントローラが必要でした。そこで、忘却ゲートと入力ゲートの操作を1つのコントローラで操作するように変更します。
2つの方針における具体的な変更は上で述べたようなものですが、この変更に伴って、別の修正を加える必要性が生まれます。具体的には、
- CECと\(h\)をまとめたため、出力ゲートによる出力制限は望ましくない。すなわち、出力ゲートの仕組みを取り除く。
- 出力ゲートを取り除くと、重み衝突が発生する可能性があるため、入力値を求めるニューロンに再帰される経路上にリセットゲートを設ける。
です。
GRUセルの構造
LSTMセルと比較できるように2つを並べて示してあります。今までと同様に、時間軸で展開していない表記と展開した表記を見てみます。
時間軸展開していない表記
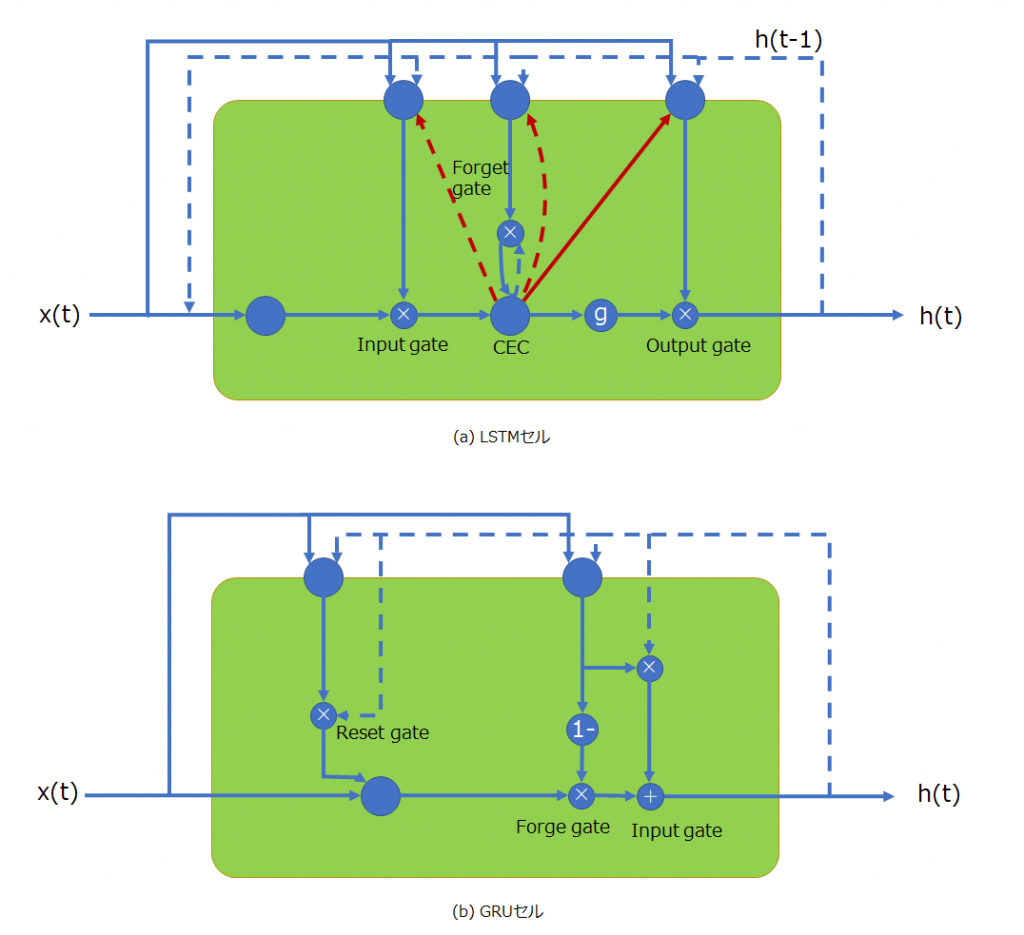
以下に時間軸展開していない表記のセルをそれぞれ示します。上がLSTMセルで、下がGRUセルです。とても簡素になっていることが分かると思います。CECセルがなくなったため、覗き穴結合はありません。注目すべき部分は、記憶の忘却と更新という操作が、1つのゲートコントローラで行われている点で、その手法は興味深いものがあります。忘却はゲートコントローラの値を1から差し引いたものを乗算することで、更新はゲートコントローラの値を1時刻前の状態ベクトルと乗算した後に加算することで実現されている点です。すなわち新たな記憶を保持するときは過去の記憶は忘れるように連動させることで構造を簡略化させています。
時間軸展開した表記
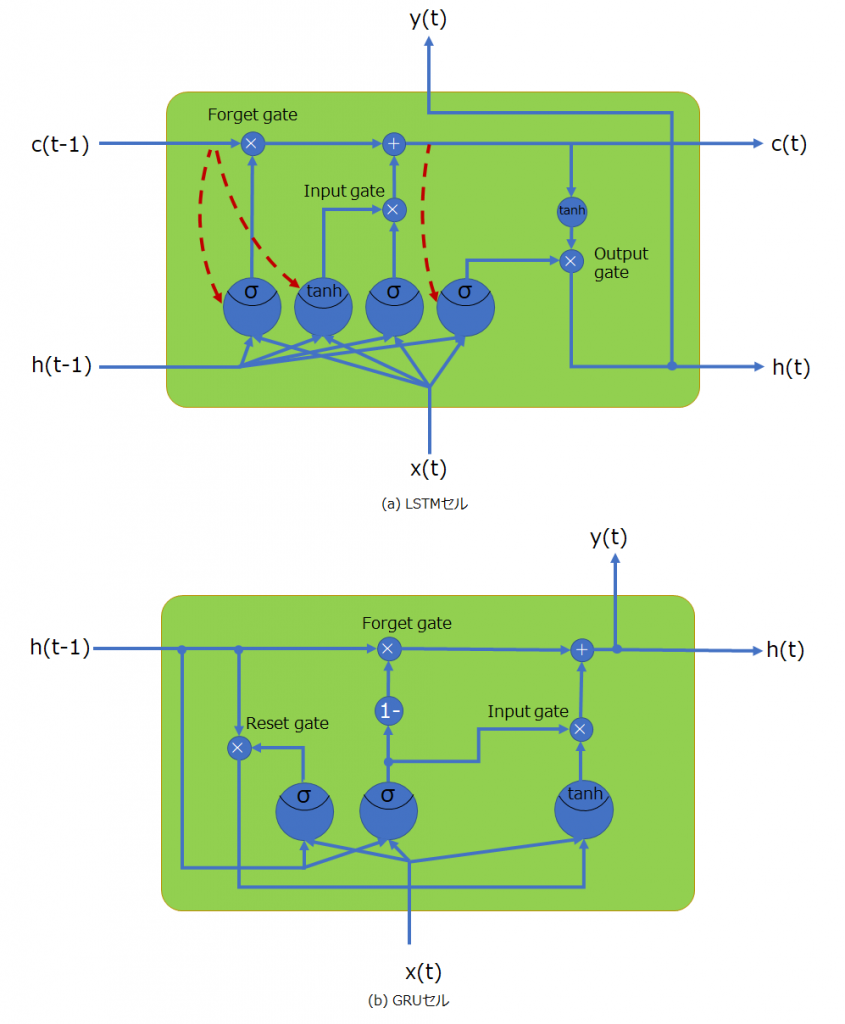
以下の図は、時間軸で展開したときの表記で、上がLSTMセル、下がGRUセルです。
GRUはLSTMに劣るのか
この点はかなり気になるところです。内部様態のバリエーションはGRUの方が確実にLSTMより少ないため、表現能力という点では落ちていると考えるべきだと思います。しかし、ハッキリとしていない部分が多く、性能は変わらないと結論付けている書籍が多くあるため、あまり気にする必要はないと思います。
念頭に置くべきことは、一般論として計算量と性能はトレードオフの関係にあるということです。絶対とは言い切れませんが、念頭に置いておくことで、壁にぶつかったときの解決策を見つけるきっかけにできるはずです。