本記事では粒子フィルタについて解説していきます。
動画でも解説しているので、よろしければご視聴いただけると嬉しいです!
粒子フィルタの概要
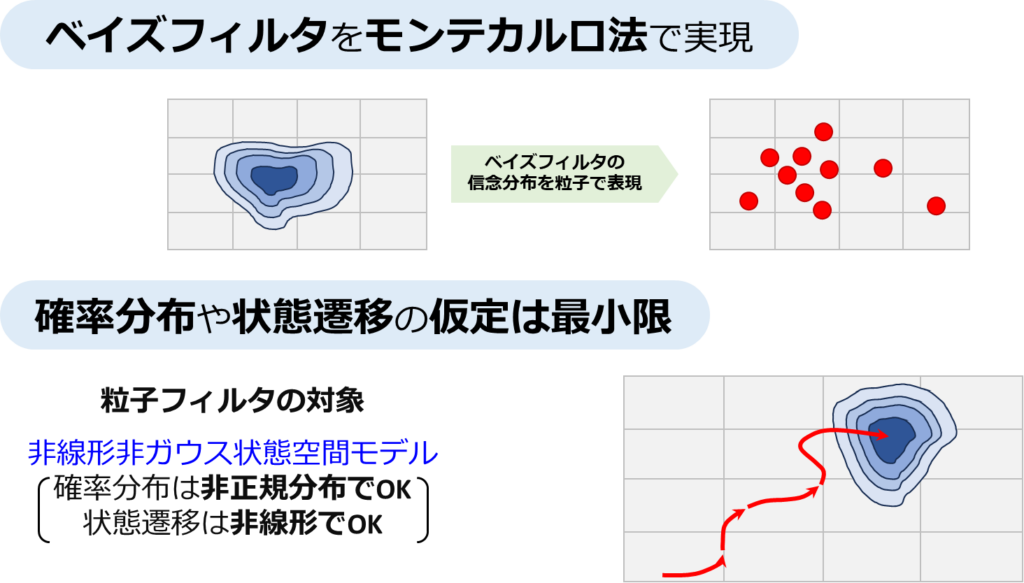
粒子フィルタとは、簡単に言えば、ベイズフィルタをモンテカルロ法を用いて実装したものです。この手法では、未知の分布を具体的な式で表現する代わりに、サンプルの集合(粒子)を用いて分布を近似します。これにより、分布の式を明確に知らなくても、その分布の変化を追跡することが可能になります。このアプローチは、計算上の利便性から派生したものであり、その有効性は広く認識されています。

ベイズフィルタとは、観測データからシステムの状態を推定するための一般的な枠組みであり、カルマンフィルタはその一例です。カルマンフィルタは線形遷移とガウスノイズの仮定に基づいており、そのため特定のシナリオに限定されます。一方、粒子フィルタはこれらの制約を設けず、確率分布や状態遷移に関する最小限の仮定のみで運用されます。その結果、粒子フィルタは正規分布に限らず、また非線形な状態遷移にも対応できるため、適用範囲が非常に広いです。
カルマンフィルタについては以下の記事で詳しく解説しています。
ベイズフィルタの基礎と状態空間モデル
ベイズフィルタの基礎と状態空間モデルについては、以下の記事で詳しく説明しているので、ぜひ、そちらを確認いただければと思います。
非線形非ガウス状態空間モデル
ここでは、非線形非ガウス状態空間モデルに焦点を当て、その特徴と利点について解説します。
非線形非ガウス状態空間モデルの利点
非線形非ガウス状態空間モデルの最大の利点は、その柔軟性にあります。カルマンフィルタが用いる線形ガウス状態空間モデルと比較すると、非線形非ガウス状態空間モデルはより複雑な現象のモデリングが可能です。例として自律移動ロボットの自己位置推定を考えると、線形ガウスモデルでは自己位置の信念を正規分布でのみ表現する必要がありますが、非線形非ガウスモデルでは、より一般的な分布を用いることができます。これは、実世界のダイナミクスが非線形であることや、観測ノイズが必ずしもガウス分布に従わないことを考慮に入れた結果です。
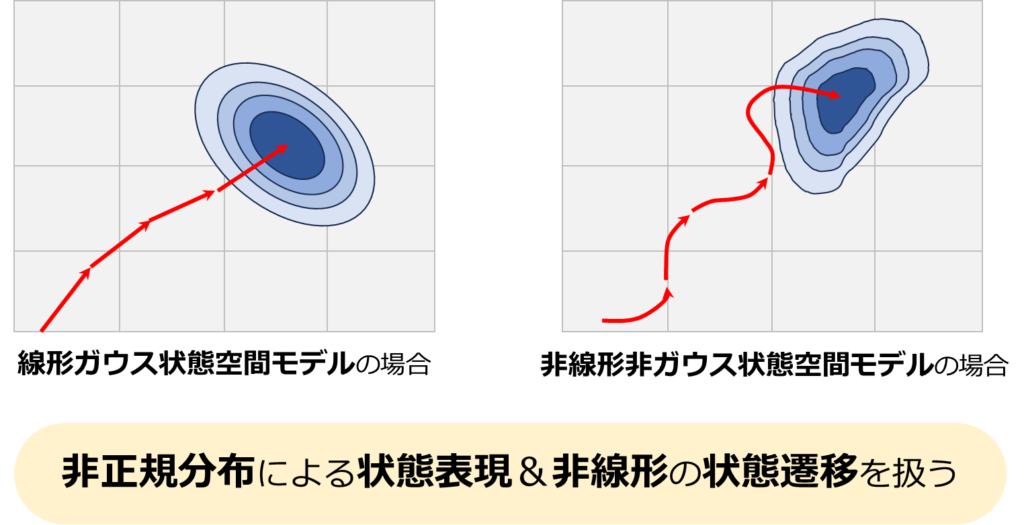
信念分布の予測の課題
しかし、非線形非ガウス状態空間モデルでは信念分布の予測が難しいという課題があります。線形ガウスモデルでは平均と共分散で分布を表現できるため、予測も比較的容易です。しかし、非ガウス分布を扱う場合、分布全体の変化を計算する必要があり、これは計算上非現実的な場合が多いです。
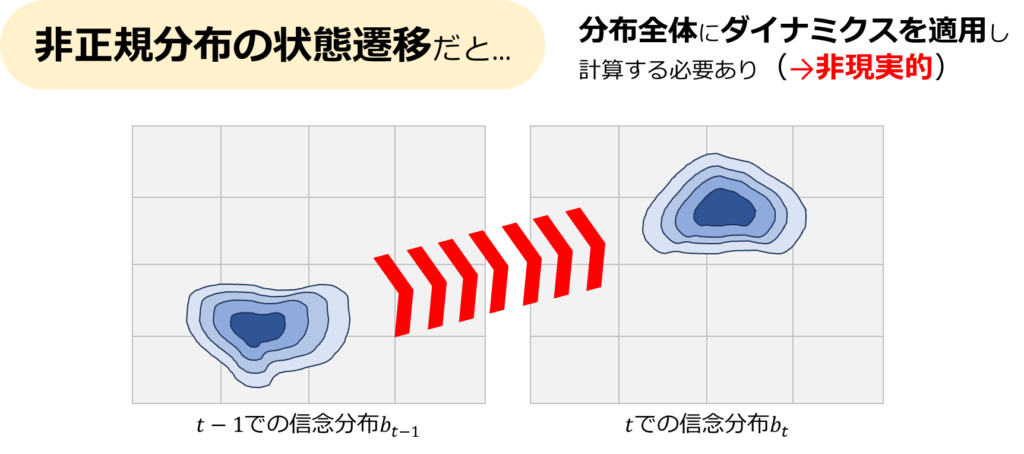
粒子フィルタの役割
この問題に対処するために、粒子フィルタ(逐次モンテカルロ法とも呼ばれる)が開発されました。粒子フィルタは、状態の推定をサンプル(粒子)の集合を通じて行うことで、非線形非ガウス状態空間モデルの計算課題を効果的に克服します。この方法では、モデルの複雑さにかかわらず、近似的だが精度の高い推定が可能になります。
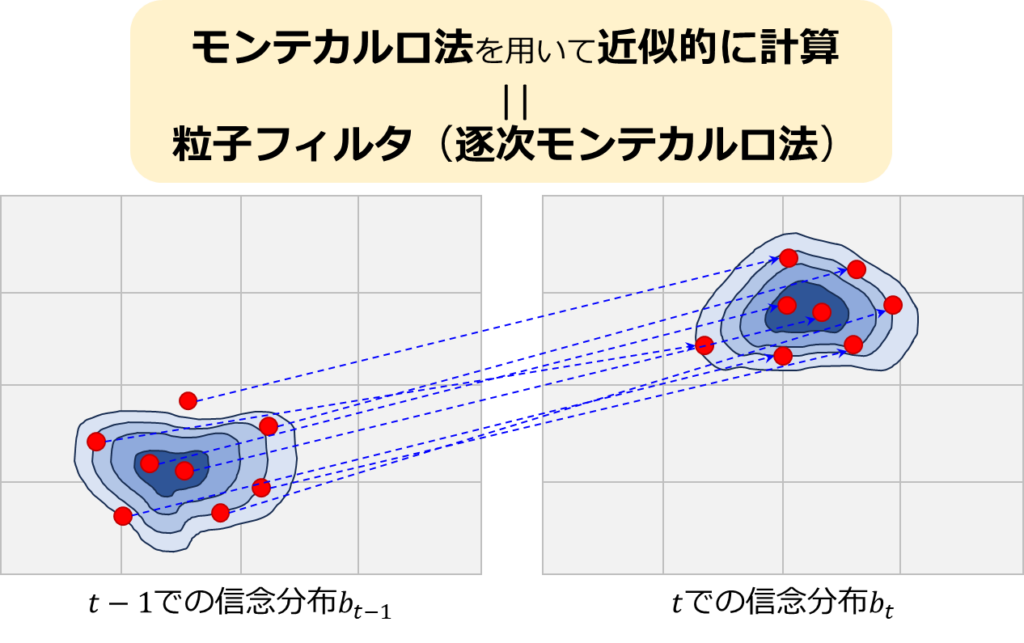
粒子フィルタの処理の流れ
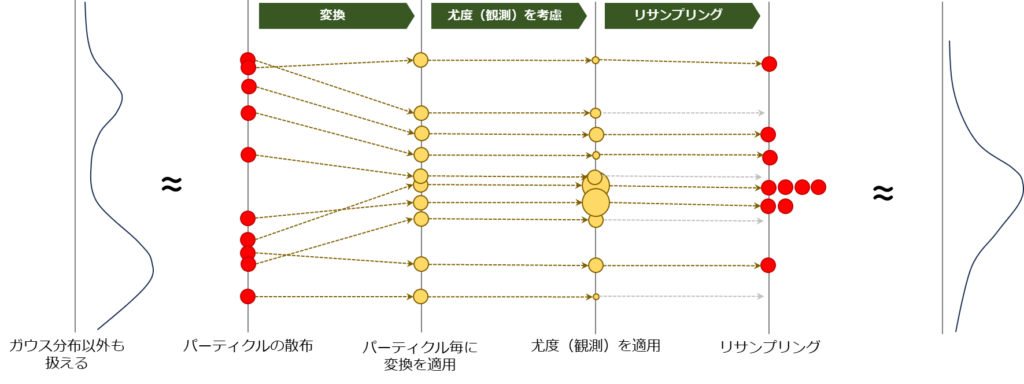
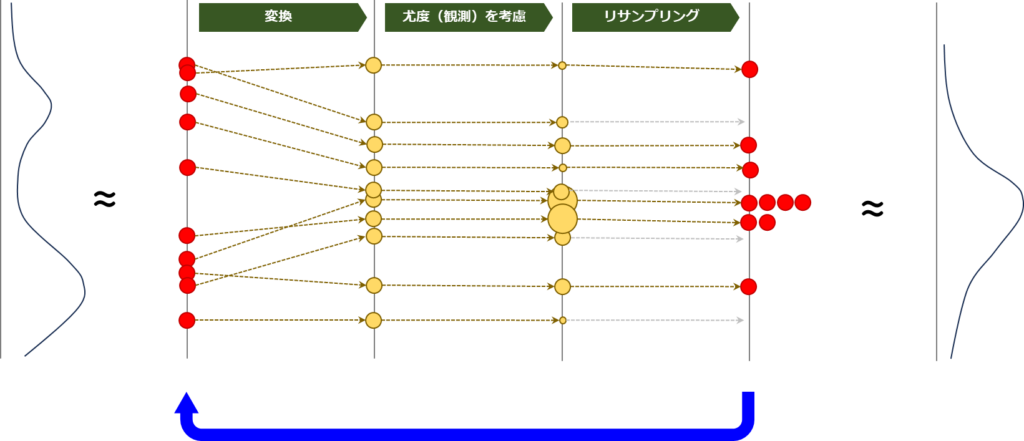
粒子フィルタを用いた信念分布の更新は、モンテカルロ法を活用して分布の変化を逐次的に追跡する方法です。具体的には、粒子フィルタは複数のステップを経て信念分布を更新します。まず、粒子を用いて現在の信念分布を近似し、次に予測モデルに基づいてこれらの粒子を変換し、さらに新しい観測データをもとに各粒子の重み(尤度に相当)を更新し、最後にこれらの重みに基づいて粒子を再サンプリングします。このプロセスを下図に示します。赤色の粒子が信念分布の近似を、黄色の粒子が変換課程での粒子をそれぞれ示しています。
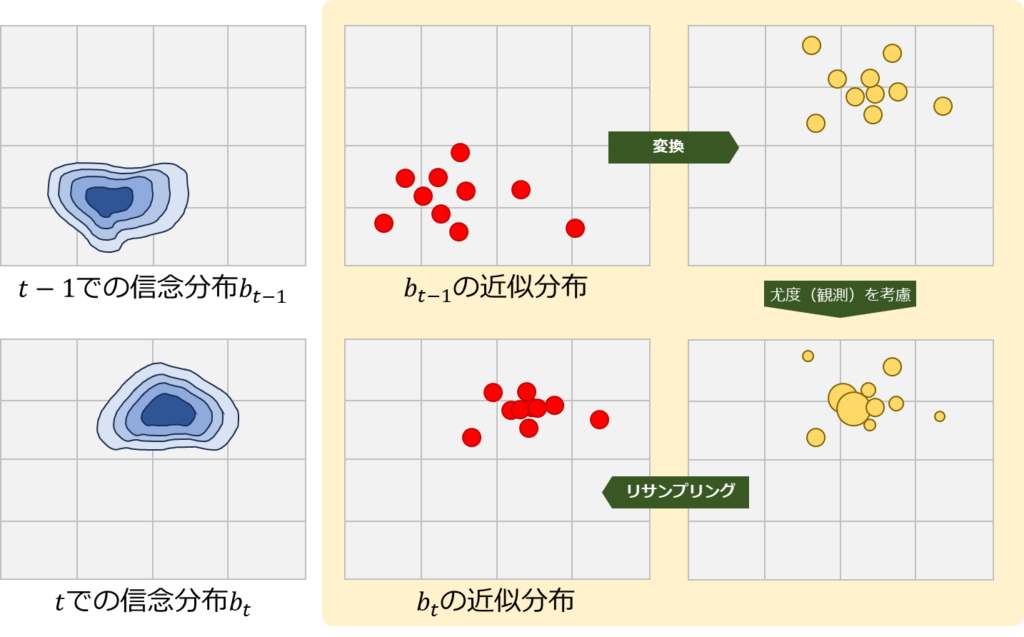
具体的な手順は次の通りです:
- 予測ステップ:時刻\(t-1\)の信念分布を粒子で近似し、これらの粒子にモデルの変換(予測モデル)を適用し、新しい粒子の集合を生成します。この時点の粒子は、まだ時刻\(t\)の信念分布を表しているわけではない点に注意が必要です。
- 更新ステップ:新たに得られた観測データに基づき、各粒子の重みを計算します。この重みは、実際の観測と粒子の予測状態との一致度(尤度)を示します。
- リサンプリングステップ:計算された重みに基づいて粒子を再サンプリングします。これにより、観測データとより一致する粒子が選択され、時刻\(t\)における信念分布のより精度の高い近似が得られます。
このプロセスを繰り返すことで、非線形非ガウス状態空間モデルの状態を逐次的に推定していきます。以下では、1次元の場合を考えて、それぞれのプロセスについて詳しく解説していきます。
状態空間が1次元の場合における粒子フィルタの処理
この章では、1次元の状態空間における粒子フィルタの適用を例にとって各ステップでの処理について説明します。
粒子による信念分布の表現
粒子フィルタにおいて、粒子の集合を使用して信念分布を近似する方法は、モンテカルロ法に基づいた非常に強力なアプローチです。この手法では、精確な分布の式を明確に定義する必要がなく、粒子の密度を通じて分布を表現します。ここで言う「粒子」とは、ディラックのデルタ関数を用いて表現される特定の点を指します。ディラックのデルタ関数は、特定の点\(x^{(i)}\)において無限大になり、それ以外の場所では0となる関数で、次のように定義されます。
$$
\delta (x-x^{(i)})=\left\{
\begin{array}{ll}
\infty & x=x^{(i)}\\
0 & x\neq x^{(i)}
\end{array}
\right.
$$
この関数により、連続空間上の個別の粒子が表現、つまり、粒子の位置においてデルタ関数が「立つ」ことで、その位置を数学的に表します。
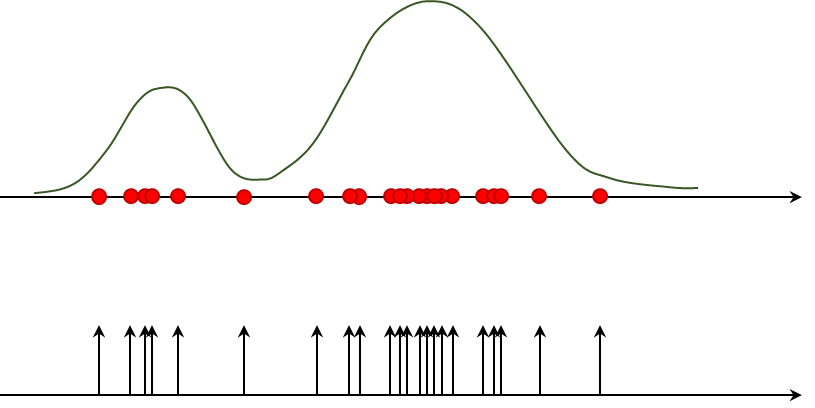
粒子を用いた信念分布の表現は、以下のように確率分布を近似する形で行われます。
$$
p(x) = \frac{1}{M}\sum_i^M\delta (x-x^{(i)})
$$
ここで、\(M\)は粒子の総数を表し、分布の積分が1になるように正規化されます。この正規化はディラックのデルタ関数の積分値が1であるため、可能になります。
※連続値で使用するディラックのデルタ関数を用いているので、より正確な式として表現するには積分記号が必要だが、粒子フィルタでは慣習としてこのように表記するのが一般的(らしい)。
この方法で確率分布を近似することに疑問を持つ人もいるかもしれませんが、重要なのは粒子の数\(M\)です。粒子の密度が高ければ高いほど、つまり粒子の数が多ければ多いほど、近似の精度は向上します。実際に、十分な数の粒子を用いることで、もともとの連続的な確率分布を非常に正確に近似することが可能になります。サンプリングされた粒子の集合が元の確率分布から得られたものと本質的に同じであると考えることができるのです。したがって、粒子の数がキーとなり、粒子フィルタの性能を大きく左右する要素の一つです。
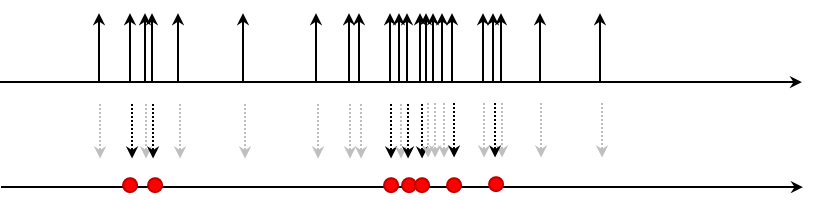
予測ステップ
システムダイナミクスの適用による予測ステップでは、粒子フィルタ内で各粒子が示す点(赤丸で近似された点)が、次の時刻にどこに移動するかを計算します。これは、各粒子に対してシステムのダイナミクスを適用し、新たな点を予測を生成するプロセスです。

更新ステップ
予測された粒子の位置に対し、尤度(観測データとの一致度)を適用しリサンプリングすることで更新ステップが行われます。このプロセスを下図に視覚化しました。各粒子の重み(尤度による影響)が変化する様子を、粒子のサイズとデルタ関数の矢印の長さで表現しています。

ここで、重み付けされた粒子を基にリサンプリングを行うと、尤度を考慮した新たな信念分布が形成されます。下図の上段は、尤度を適用して粒子に重みがついている様子を、中段は上段からサンプリングしてきた様子を、下段は、中段からデルタ関数の表示を消して、粒子だけにしたものです。
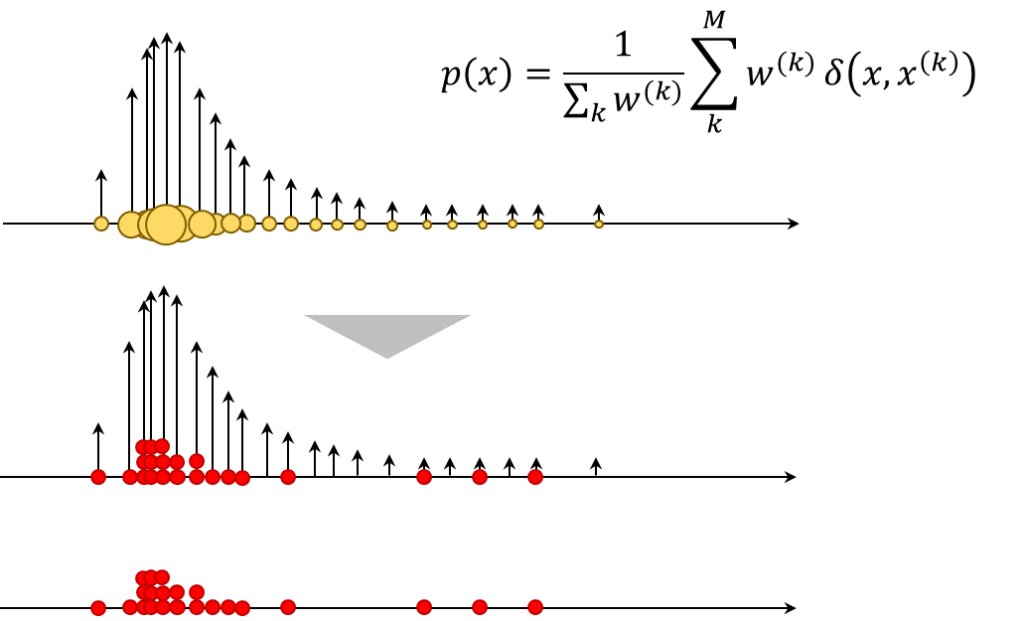
予測と更新による逐次的な信念分布の推定
粒子を用いた信念分布の予測と更新プロセスをご理解いただけたかと思います。粒子フィルタでは、予測と更新を繰り返すことにより、逐次的に実行されます。これは、下図の青色矢印で示されている通りです。
まとめ
ここまでの内容を簡潔にまとめると、粒子フィルタはベイズフィルタの概念をモンテカルロ法で近似する手法です。このアプローチにより、カルマンフィルタに見られるような大きな制約なしに、様々な分布や動きを捉えることが可能となります。粒子は連続空間上の点として数学的に扱われ、ディラックのデルタ関数を用いて信念分布を表現します。予測ステップでは、これらの点(デルタ関数)の位置を更新し、観測データに基づき各点の重みを再計算します。この重み付けを通じて粒子を再サンプリングすることで、新たな信念分布を形成します。粒子フィルタは、このプロセスを繰り返し実行することで動作します。
本記事の内容は以上です。ベイズフィルタやカルマンフィルタについては別の記事解説しているので、気になる方はそちらを見ていただければと思います。
最後までお読みいただきありがとうございました。


