本記事では、カルマンフィルタの基礎について解説しました。
解説動画も出していますので、ぜひご覧ください!
カルマンフィルタのモチベーション
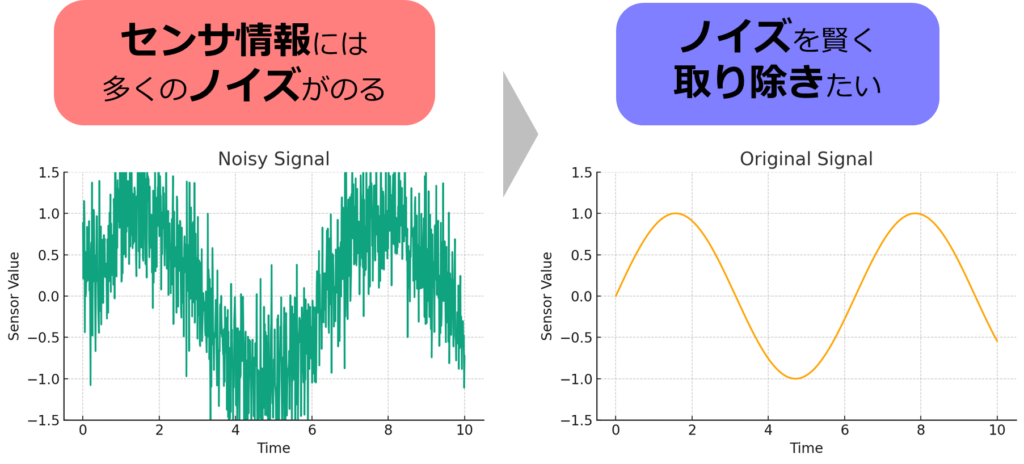
センサーからの情報には多くのノイズが含まれており、これをそのまま利用することは好ましくありません。目指すべきは、ノイズのない、真の情報を把握することにあります。しかし、このノイズフリーな状態を直接得ることはできません。このため、目に見えない「隠れ状態」としてこれを推定する必要があります。これについては、ベイズフィルタに関する以前の記事で状態推定問題として触れましたが、ベイズフィルタはその理論的基盤を提供するものであり、実際の実装にはコンピュータで扱える形式に落とし込む必要があります。カルマンフィルタは、この要求を満たす形でベイズフィルタの概念を実用化したものです。
ベイズフィルタについて知りたい方は以下の記事を参考にしてください。
具体例として4脚ロボットの姿勢推定を取り上げます。4脚ロボットにおける姿勢推定は、その動作の基礎を成します。一般的に4脚ロボットは、IMU(慣性測定ユニット)を搭載しており、位置決めと姿勢制御に不可欠な役割を果たしています。四脚ロボットがバランスを保ちながら効率的に移動するためには、正確な姿勢情報が必須です。この情報は、IMUなどの慣性センサから得られます。慣性センサは種類が豊富で、趣味のロボット製作などでよく用いられるIMUの例としてMPU6050の写真を以下に載せましたが、これらのセンサから得られるデータには多くのノイズが伴うことが多いです。そのため、センサから得た生データをそのまま姿勢情報として扱うのは適切ではありません。そのため、ノイズを含んだデータから正確な姿勢を推定するプロセスが必要となります。ここでカルマンフィルタが役立ちます。カルマンフィルタを使用することで、ノイズを含む観測データから、ノイズを可能な限り取り除いた姿勢情報をリアルタイムに推定することができます。さらに高い精度の姿勢推定を実現するためには、つま先の接触センサーを活用するなどの追加の工夫が行われることがあります。


線形ガウス状態空間モデル
線形ガウス状態空間モデルを理解する前に、予測、フィルタリング、平滑化の違い、ベイズの定理、ベイズフィルター、そして状態空間モデルの基本概念を把握しておくことが重要です。これらの基礎に関しては、ベイズフィルターの基本を扱った別の記事で詳しく解説していますので、そちらを参照してください。
本稿では、線形ガウス状態空間モデルにフォーカスして説明を進めます。このモデルは、部分観測マルコフ決定過程(POMDP)の枠組みにおいて、状態遷移の線形性とノイズのガウス性を仮定した具体的なモデリング手法です。モデルは主に二つの方程式で構成されます。
システム方程式
$$
\boldsymbol{x}_t = \boldsymbol{Ax}_{t-1} + \boldsymbol{Bu}_t + \boldsymbol{w}_t
$$
これは状態遷移を示す式で、次の状態\(\boldsymbol{x}_t\)は前の状態\(\boldsymbol{x}_{t-1}\)、制御入力\(\boldsymbol{u}_t\)、およびノイズ\(\boldsymbol{w}_t\)の線形結合で表されます。
観測方程式
$$
\boldsymbol{z}_t = \boldsymbol{Hx}_t + \boldsymbol{v}_t
$$
これは観測値\(\boldsymbol{z}_t\)が現在の状態\(\boldsymbol{x}_t\)とノイズ\(\boldsymbol{v}_t\)の線形結合で得られることを示します。
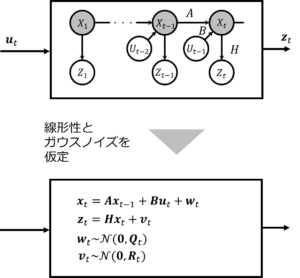
ここで、\(\boldsymbol{A},\boldsymbol{B},\boldsymbol{H}\)は時間によらず一定であり、ノイズはガウス分布に従うと仮定されています(\(\boldsymbol{w}\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{R}), \boldsymbol{v}\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{Q})\))。
今説明したことを、図にすると以下のようになります。このモデルの適用にあたっては、対象システムが線形ガウス状態空間モデルの仮定に適合している必要があります。対象がこのモデルで表せない場合、完全に不適合というわけではありませんが、非線形や非ガウス性を取り扱う他のモデル、例えば粒子フィルタなどの使用が適切かもしれません。
粒子フィルタについては以下の記事で解説しています。
カルマンフィルタ
カルマンフィルタは、線形ガウス状態空間モデルに基づいて、状態変数\(X\)の確率分布を推定することを目的としています。文章中で状態変数が大文字または小文字で表記される場合がありますが、これは同一のものを指しており、確率変数を表す際に慣例的に大文字を用いるためです。

カルマンフィルタの2ステップ
カルマンフィルタは、予測と更新の二つの主要なステップを繰り返し行うプロセスによってフィルタリングします。このプロセスは、直感的に理解すると、直前の状態から次の状態への移行を予測し、新たに得られた観測情報を用いてこれらの予測を修正することを繰り返すものです。具体的には、予測プロセスではシステム方程式を用いて未来の状態を予測し、更新(フィルタリング)プロセスでは観測方程式に基づき実際に得られた観測データを取り入れて、推定値の精度を高めます。更新の際には、カルマンゲインと呼ばれる重み付け係数を計算し、このゲインを用いて状態の平均値と分散(共分散)を更新します。このカルマンフィルタの基本的な動作原理は、連続的な予測と更新のサイクルによって、不確実性の中でも最も可能性の高い状態推定値を得ることにあります。

以降では、この図に登場した式について詳細を説明していきます。
予測プロセス
まずは、予測プロセスの式から導出を行いましょう。予測プロセスでは、システムダイナミクスを用いて、次状態の確率分布を計算します。
状態変数\(X\)の推定にあたっては、まず制御入力\(\boldsymbol{u}_t\)を確定的なものとして捉え、状態\(\boldsymbol{x}_{t-1}\)の分布を考えます。初期分布にガウス分布を仮定すると、システム方程式による線形変換の繰り返しによって、状態\(X\)の分布もガウス分布を保持します。これは、正規分布の線形変換が再び正規分布になる性質に基づいています。カルマンフィルタの予測プロセスでは、この性質を利用して状態の平均\(\hat{\boldsymbol{x}}_t^-\)と分散\(\boldsymbol{P}_t^-\)(多変量正規分布では平均ベクトルと共分散行列)を推定します。
では、まず状態の平均について考えます。平均に関しては、記号上で区別をつけるために予測値にはハット記号を上に、そして予測の更新前を示すためにマイナス記号を付けます。具体的には、次の式によって平均が計算されます。
$$\begin{eqnarray}
\hat{\boldsymbol{x}}_t^- &=& \mathbb{E}[\boldsymbol{x}_t | \boldsymbol{x}_{1:t}, \boldsymbol{u}_t]\\
&=& \mathbb{E}[\boldsymbol{Ax}_{t-1} + \boldsymbol{Bu}_t + \boldsymbol{w}_t] \\
&=& \boldsymbol{A}\mathbb{E}[\boldsymbol{x}_{t-1}] + \boldsymbol{B}\mathbb{E}[\boldsymbol{u}_t] + \mathbb{E}[\boldsymbol{w}_t] \\
&=& \boldsymbol{A}\hat{\boldsymbol{x}}_{t-1} + \boldsymbol{B}\boldsymbol{u}_t
\end{eqnarray}$$
この式では、\(\hat{\boldsymbol{x}}_{t-1}\)は直前の時刻で観測に基づき微調整された推定値を示し、制御入力\(\boldsymbol{u}_t\)は確定的なものと仮定され、システムノイズの平均は0と仮定されるため、最終的には最終行の式に簡略化されます。
次に、分散ですが、これは
$$\begin{eqnarray}
\boldsymbol{P}_t^- &=& \mathbb{E}[(\boldsymbol{x}_t - \hat{\boldsymbol{x}}_t^-)(\boldsymbol{x}_t - \hat{\boldsymbol{x}}_t^-)^T]\\
&=& \mathbb{E}[(\boldsymbol{Ax}_{t-1} + \boldsymbol{Bu}_t + \boldsymbol{w}_t - \boldsymbol{A}\hat{\boldsymbol{x}}_{t-1} - \boldsymbol{B}\boldsymbol{u}_t)(\boldsymbol{Ax}_{t-1} + \boldsymbol{Bu}_t + \boldsymbol{w}_t - \boldsymbol{A}\hat{\boldsymbol{x}}_{t-1} - \boldsymbol{B}\boldsymbol{u}_t)^T]\\
&=& \mathbb{E}[(\boldsymbol{A}(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})+ \boldsymbol{w}_t )(\boldsymbol{A}(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})+ \boldsymbol{w}_t )^T]\\
&=& \mathbb{E}[(\boldsymbol{A}(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})+ \boldsymbol{w}_t )((\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})^T\boldsymbol{A}^T+ \boldsymbol{w}_t^T)]\\
&=& \mathbb{E}[\boldsymbol{A}(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})^T\boldsymbol{A}^T + \boldsymbol{A}(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})\boldsymbol{w}_t^T + \boldsymbol{w}_t(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})^T\boldsymbol{A}^T + \boldsymbol{w}_t\boldsymbol{w}_t^T]\\
&=& \boldsymbol{A}\mathbb{E}[(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})(\boldsymbol{x}_{t-1} -\hat{\boldsymbol{x}}_{t-1})^T]\boldsymbol{A}^T + \mathbb{E}[\boldsymbol{w}_t\boldsymbol{w}_t^T]\\
&=& \boldsymbol{A}\boldsymbol{P}_{t-1}\boldsymbol{A}^T + \boldsymbol{Q}_t
\end{eqnarray}$$
のように表されます。以上より、予測プロセスにおける平均と共分散行列を導くことができました。
この予測値は、実測された観測を用いて更新、すなわちフィルタリングする必要があります。次では、その式の導出を行います。
更新(フィルタリング)プロセス
更新プロセスでは、カルマンフィルタの中核となるカルマンゲインの計算が行われます。このプロセスにおける目的は、新たに得られた観測データを用いて、予測された状態推定値を修正することです。カルマンフィルタは、以下のステップでこの更新を行います。
カルマンゲイン\(\boldsymbol{K}_t\)を用いて状態推定値を更新する式は以下の通りです。
$$
\hat{\boldsymbol{x}}_t = \hat{\boldsymbol{x}}_t^- + \boldsymbol{K}_t(\boldsymbol{z}_t - \boldsymbol{z}_{pt}) = (1-\boldsymbol{K}_t\boldsymbol{H})\hat{\boldsymbol{x}}_t^- + \boldsymbol{K}_t\boldsymbol{z}_t
$$
ここで、\(\boldsymbol{z}_t\)は時刻\(t\)における新たな観測値、\(\boldsymbol{H}\)は観測モデルを表す行列です。式中の\(\boldsymbol{z}_t - \boldsymbol{z}_{pt}\)は観測残差を表し、予測された観測と実際の観測との差を示します。
カルマンゲインの計算は、更新プロセスで得られる状態推定値\(\hat{\boldsymbol{x}}_t\)の分散を最小化することによって行われます。分散の最小化は、推定プロセスにおける不確実性が最低に抑えられることを意味し、これは推定の精度が向上することと同義です。カルマンゲインの最適値を求めるために、\(\hat{\boldsymbol{x}}_t\)の分散をカルマンゲインについて偏微分し、その結果が0になる点を探します。この点が分散を最小にするカルマンゲイン、すなわち最適カルマンゲインです。この導出過程は、ここでは紹介しませんが、分散の偏微分によって得られる等式を解くことで、複雑な式変形を経て最適カルマンゲインを導出することが可能です。
$$
\boldsymbol{K}_t = \frac{\boldsymbol{P}_t^-\boldsymbol{H}^T}{\boldsymbol{HP}_t^-\boldsymbol{H}^T+\boldsymbol{R}_t}
$$
ここで、\(\boldsymbol{P}_t^-\)は予測された誤差共分散、\(\boldsymbol{R}\)は観測ノイズの共分散を表します。
カルマンゲインを用いて更新された状態推定値の分散(誤差共分散)は以下の式によって更新されます。
$$
\boldsymbol{P}_t = (\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H})\boldsymbol{P}_t^-
$$
この式は、新しい観測を考慮して推定値の不確実性をどのように減少させるかを示しています。カルマンフィルタによるこの更新プロセスを通じて、システムの状態推定値は連続的に精度を高められていきます。以上が、カルマンフィルタの更新プロセスの詳細です。
まとめ
まとめると、カルマンフィルタの本質は予測と更新のプロセスを繰り返すことにあり、この連続したプロセスの中心には「カルマンゲイン」の計算があります。カルマンゲインは、ベイズフィルタリングの枠組み内、特に線形ガウス状態空間モデルにおける更新プロセスで、新たに得られた観測データの信頼度を定める決定的な役割を果たします。適切なカルマンゲインの計算によって、状態推定の精度は最大化され、不確実性は最小化されます。

カルマンフィルタの方程式やカルマンゲインの計算は初見では複雑に見えるかもしれません。しかし、この記事を通じて、これらの概念の導出方法、形式の理由、そしてカルマンゲインが更新プロセスをどのように最適化するかの理解が深まりましたら幸いです。
最後までお読みいただきありがとうございました。