この記事では、ベイズフィルタについて詳しく学びたい方向けに、ベイズフィルタが解決しようとする問題とその動機から始めて、ベイズフィルタによる解法へと説明を行います。具体的な解法を理解するために、状態空間モデルの概念を取り入れ、様々な場面でのベイズフィルタの式を導出します。そして、ロボットの自己位置推定を例に取り上げて、ベイズフィルタを用いた位置推定の理解を深めていきます。
本記事の内容は動画でも解説していますので、もしよければそちらもご覧ください。
状態推定問題とベイズフィルタ
状態推定問題は、移動ロボットやその他のシステムが自身の状態(位置、速度、姿勢など)を正確に把握するために必要な基本的な問題です。この問題では、システムが直接自身の状態を完全に知ることはできません。代わりに、センサーからの観測を通じて、間接的に状態を推定します。しかし、センサーからのデータにはノイズや不確実性が含まれており、これらを考慮して精度の高い状態推定を行う必要があります。
このような課題に対処するために、ベイズフィルタの概念が非常に重要となります。ベイズフィルタは、センサデータの不確実性を数学的に扱い、より正確な推定を行うための抽象的なフレームワークを実現します。実際にベイズフィルタを適用する際には、カルマンフィルタや粒子フィルタなどの具体的な手法が用いられます。これらの手法は、ベイズフィルタの原理を基にしており、多岐にわたる応用が可能です。
ベイズフィルタの応用例としては、ロボットの自己位置推定やモータの角度推定があります。基本的に、センサデータはノイズを含むため、ベイズフィルタを使用して不確実性を管理しながら、信頼できる情報を抽出することができます。このように、ベイズフィルタは不確かな情報から確実性を高めるための強力なツールと言えるでしょう。

ベイズフィルタの使用目的やモチベーションを把握したところで、一歩踏み込んで、フィルタリングが具体的に何を意味するのかを、また、予測や平滑化とどう異なるのかについて、疑問をお持ちの方もいるかもしれません。ですので、次で詳しく説明します。
予測・フィルタ・平滑化
先にベイズフィルタを用いた位置推定問題について説明しましたが、ベイズフィルタの使用範囲はそれに留まらず、より広い「状態推定問題」に適用されます。具体的には、直接観測が不可能な「状態」を推定する問題になります。ここでは、状態推定手法について概説し、予測・フィルタリング・平滑化の違いについて説明します。
状態推定には主に三つの方法があります。それは、予測、フィルタリング、平滑化です。これらの概念の違いを理解することは、データ解析やシステムモデリングにおいて非常に重要です。
- 予測は、時刻\(t-1\)までの情報を基にして、時刻\(t\)での状態を推定するプロセスです。未来の予測に役立ちます。
- フィルタリングは、時刻\(t\)までのデータを使用して、その時点での状態を推定することです。これはリアルタイムの状態推定に有用で、最新の情報に基づいて判断が必要な場合に活用されます。
- 平滑化は、未来のデータを含む過去の全データを再評価し、特定の時点での状態をより正確に推定する方法です。これにより、過去の状態のより詳細な理解が可能になります。
これらの手法は、ある時点の状態を推定するという共通の目的を持ちながらも、使用するデータの範囲が異なります。ベイズフィルタは主にフィルタリングに分類され、時刻\(t\)までの観測データを用いて、その時点の状態を推定する技術です。
下図は今説明した内容を図に表したものです。\(O\)は観測を、\(S\)は状態を表しています。状態ノードの背景が灰色なのは、それが実際には知れない隠れ状態であることを表しています。詳細は、後ほど説明します。
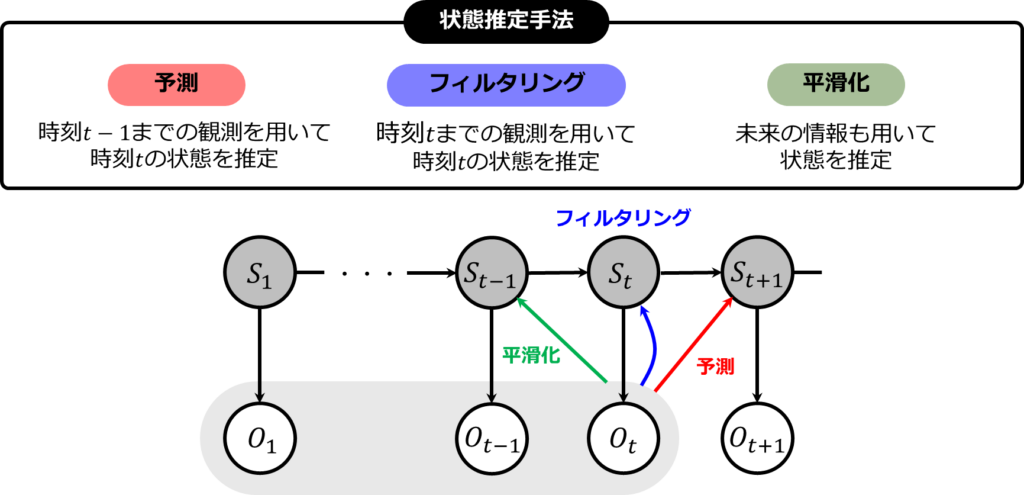
ここで、ベイズフィルタという名前についている"フィルタ"の意味についてご理解いただけたと思います。では、ベイズフィルタの詳細を理解するための第一歩として、次はベイズの定理について解説します。
ベイズの定理
ベイズフィルタを理解するには、ベイズの定理について理解している必要があります。この定理は、新たな情報が得られたときに、ある仮説の確率をどのように更新するかを教えてくれる数学的な枠組みを表します。
ベイズの定理は、事象\(B\)が起こった後に事象\(A\)の発生確率を更新する方法について述べています。この理論的な背景を持つことで、我々は不確実性の中でもより情報に基づいた推測を行うことが可能になります。具体的な数式は以下の通りです
$$
P(A|B) = \frac{P(B|A)P(A)}{P(B)}
$$
ここで、
| \(P(A|B)\) | 事象\(B\)が起きた条件下での事象\(A\)の起きる確率(事後確率) |
| \(P(B|A)\) | 事象\(A\)が起きた条件下での事象\(B\)の起きる確率(尤度) |
| \(P(A)\) | 事象\(A\)が起きる確率(事前確率) |
| \(P(B)\) | 事象\(B\)が起きる確率(周辺確率) |
ベイズフィルタの意義としては、不確実性のもとでの意思決定や、観測を用いた確率モデルの信念(=状態の確率分布)の更新が行える点です。
応用例としては、疾患の診断、感情推定、スパムメールのフィルタリング、ロボットの自己位置推定などがあります。
ベイズの定理は、とても基礎的な概念ですが、これがベイズフィルタのほぼすべてを表しています。
ベイズフィルタとベイズの定理
ベイズフィルタとベイズの定理の関係性について、分かりやすく解説します。
まず、ベイズフィルタの基本をおさらいしましょう。これは、センサなどの観測データを基に、状態を逐次的に推定する手法です。このプロセスは、ベイズの定理を活用しています。例として、「人の感情推定」を考えてみましょう。
ある情報に基づいて、ある人の感情を予測します。この初期予測をXとしますが、この段階では確信に欠け、あくまで仮説に過ぎません。次に、その人に実際に会った際の観測データから、感情が予測Xとは異なることが明らかになり、感情をYに更新します。この更新プロセスがフィルタリングに相当し、これを繰り返すことがベイズフィルタの本質です。このプロセス全体がベイズの定理に基づいています。
具体的には、事前に予測した感情\(P(A)\)を実際の観測データ\(P(B|A)\)に基づいて更新するプロセスです。感情の状態には「喜び」「平静」「悲しみ」「怒り」などがあり、\(P(A)\)はこれらの事前確率を示します。一方で\(P(B|A)\)は、観測データ(例えば、笑顔や元気な歩き方など)を指し、これらのデータが特定の感情状態においてどれくらいの頻度で観察されるかを示します。この情報をもとに、感情の状態を更新するわけです。
この例を通じて、ベイズフィルタとベイズの定理がどのように実世界の問題解決に応用されるかがお分かりいただけたでしょう。理論だけでなく、具体的な事例を挙げることで、これらの概念がより理解しやすくなったはずです。
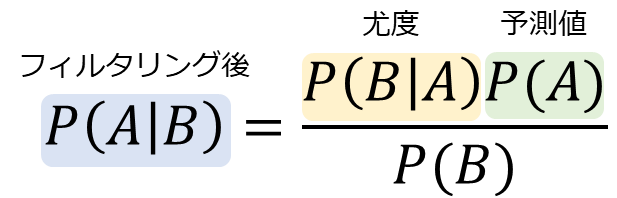
次に、具体的なシナリオを想定し、フィルタの式について詳しく説明します。ここでは、状態空間モデルという重要な概念が登場します。このモデルを理解することで、特定の状況下でのフィルタリングがどのように機能するかをより深く掘り下げることができます。
状態空間モデルの基本
状態空間モデルとは、システムの挙動を確率的に推論するための枠組みです。このモデルは、システムが時間とともにどのように変化するかを記述する「状態空間」と、その変化を捉える仕組みを提供します。主な例として、隠れマルコフモデル(Hidden Markov Model; HMM)や部分観測マルコフ決定過程(Partially Observable Markov Decision Process; POMDP)があります。
隠れマルコフモデルは、直接観測できない「隠れ状態」に基づいて、我々が観測可能なデータが生成されると考えます。ここで重要なのは、隠れ状態がマルコフ性を持つという仮定です。これは、隠れ状態の推定をマルコフ性があると仮定して行うということを意味します。
一方、部分観測マルコフ決定過程は、隠れマルコフモデルに意思決定のプロセスを組み合わせたものです。このモデルでは、行動を通じてシステムの状態遷移をコントロールできると考えられています。つまり、行動の選択によって、システムの未来が変わることを扱います。
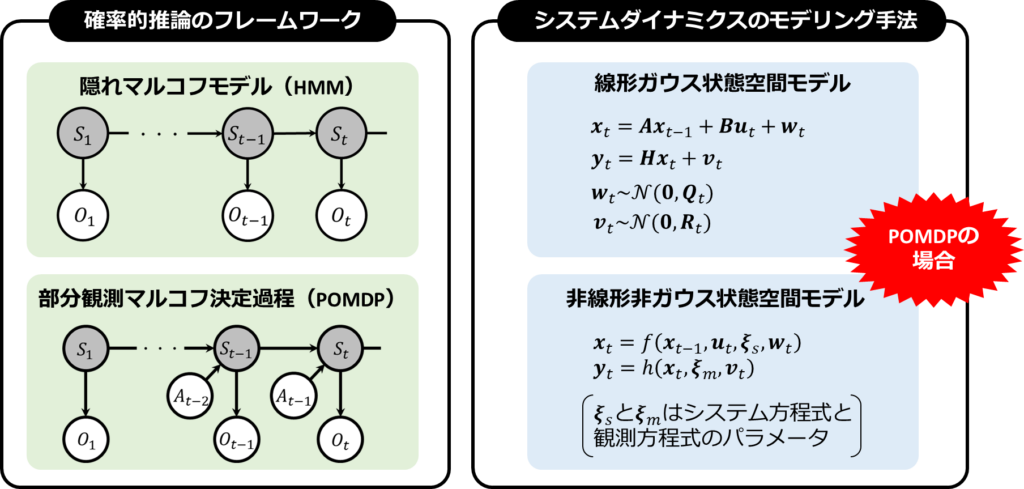
これらのモデルは、システムの動的な挙動を理解するための強力なツールです。具体的なモデリング手法としては、線形ガウス状態空間モデルや非線形非ガウス状態空間モデルがあり、これらはカルマンフィルタや粒子フィルタなどの詳細な解析手法へとつながります。今回はこれらの手法に深入りしませんが、状態空間モデルが分析の基礎となることを理解していただければと思います。
カルマンフィルタや粒子フィルタについては以下の記事で解説しています。
次に、隠れマルコフモデルや部分観測マルコフ決定過程について、より詳しく掘り下げて説明していきます。
隠れマルコフモデル
隠れマルコフモデルを理解するためには、まずマルコフモデル(Markov Model; MM)の概念を把握することが重要です。マルコフモデルでは、ある時点での状態が直前の時点の状態にのみ依存するとされています。この特性をマルコフ性と呼び、状態がこのマルコフ性を持つ場合、それをマルコフモデルと称します。
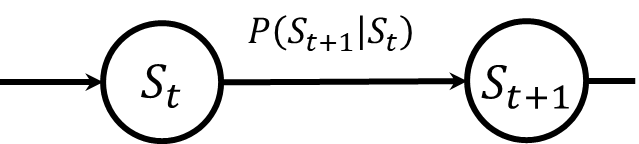
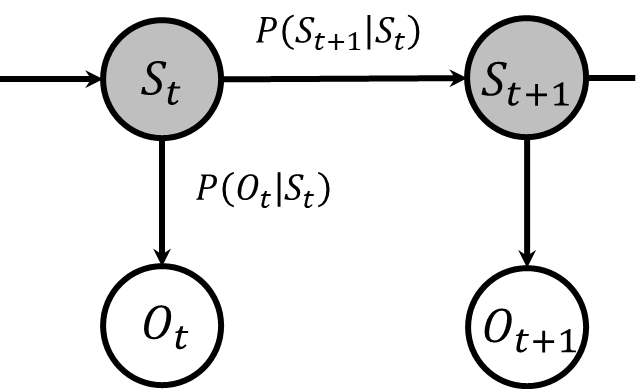
世の中の多様な現象をマルコフモデルで表現しようとする際には限界があります。いくら努力しても、マルコフモデルでは表現が難しい、または不可能な現象が存在します。こうした状況で重要になるのが、隠れマルコフモデルです。隠れマルコフモデルでは、直接観察することができないマルコフ性を持つ状態があり、その状態から生成される観測データを私たちが得ることができます。このモデルは、隠れ状態が直接観察できないため、状態のノードを灰色で表現しています。観測データ自体はマルコフ性を持ちませんが、隠れマルコフモデルを用いることで、観測される現象の背後にあるマルコフ性を持つ状態を推測することが可能になり、適用範囲が広がります。特に音声認識などの分野でその有用性が認められています。
部分観測マルコフ決定過程
マルコフモデルや隠れマルコフモデルでは、状態が自動的に変化していくシナリオを扱いますが、これらのモデルは人間のように主体的に行動し、環境に積極的に影響を与えるエージェントをモデル化するには不向きです。この課題に対処するために、意思決定プロセスをモデルに組み込むことが求められます。意思決定の過程を取り入れたマルコフモデルがマルコフ決定過程(Markov Decision Process; MDP)であり、さらに、状態が直接観測できない場合のモデルが部分観測マルコフ決定過程です。
マルコフ決定過程は、状態、行動、報酬から成るシステムを指します。これは強化学習の問題にも用いられる非常に重要な確率モデルで、現在の状態における行動の選択が、受け取る報酬や次の状態への遷移を決定します。
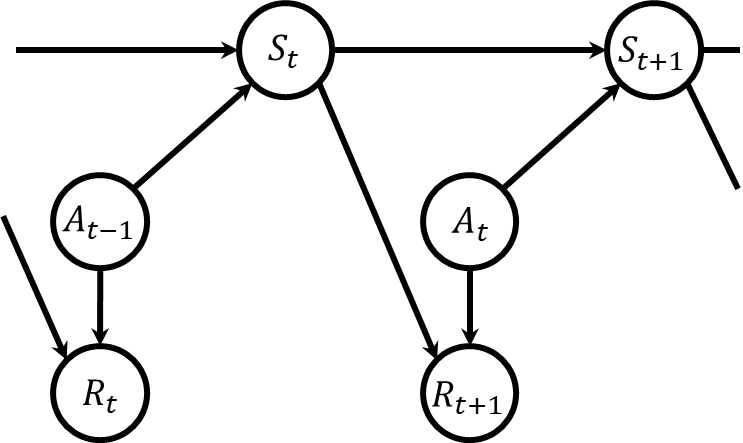
この記事では状態推定問題に焦点を当てています。そのため、状態が直接観測可能なマルコフ決定過程は主な対象ではなく、ここで重要となるのは状態が直接見えないマルコフ決定過程、すなわち部分観測マルコフ決定過程です。この過程は下図で示される通りです。つまり、マルコフ決定過程の状態は隠れ状態へと変わり、新たに観測が追加され、その観測は直前の時刻の行動と、その遷移後の隠れ状態に基づいて決定されます。
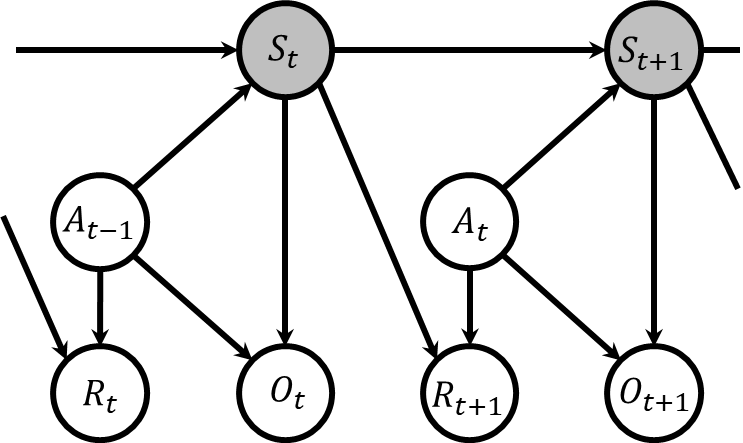
状態推定問題では、報酬の概念はあまり重要ではないため、しばしば部分観測マルコフ決定過程から報酬を除外した形で扱われます。また、行動から観測への直接的な矢印も省略されることが多く、これにより単純化されたモデルが用いられます。したがって、状態推定問題において言及される部分観測マルコフ決定過程は、以下のような単純化された形態を指すことが一般的です。
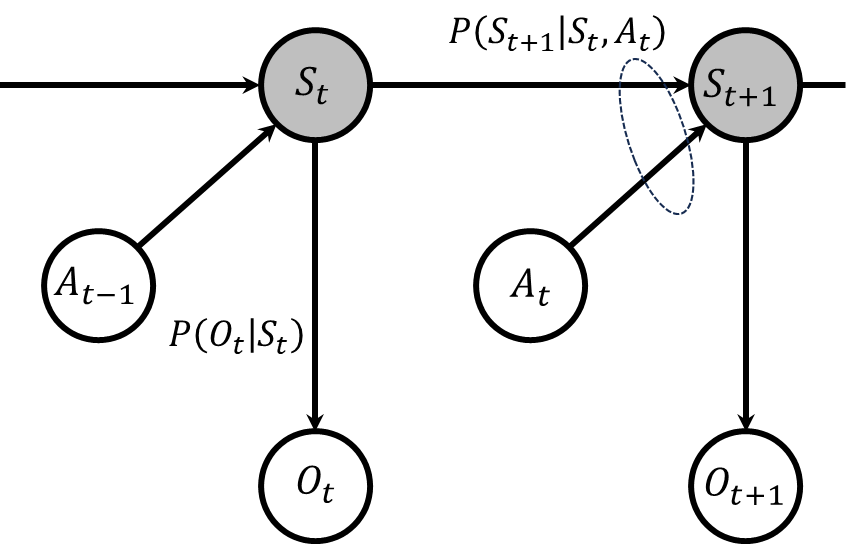
これまでに、状態空間モデルの典型的な例として隠れマルコフモデルと部分観測マルコフ決定過程を紹介しました。次に、これらのケースにおいてベイズフィルタをどのように適用するかについて説明します。
ベイズフィルタによる状態推定
隠れマルコフモデルの状態推定
隠れマルコフモデルにおける状態推定をベイズフィルタを使用して行う方法について見ていきましょう。
隠れマルコフモデルのフィルタリングでは、現在の時刻までに得られた観測データを基に、現在の時刻における状態を推定します。
式で示すと、以下のようになります。
$$
F(S_t) = P(S_t|O_{1:t})
$$
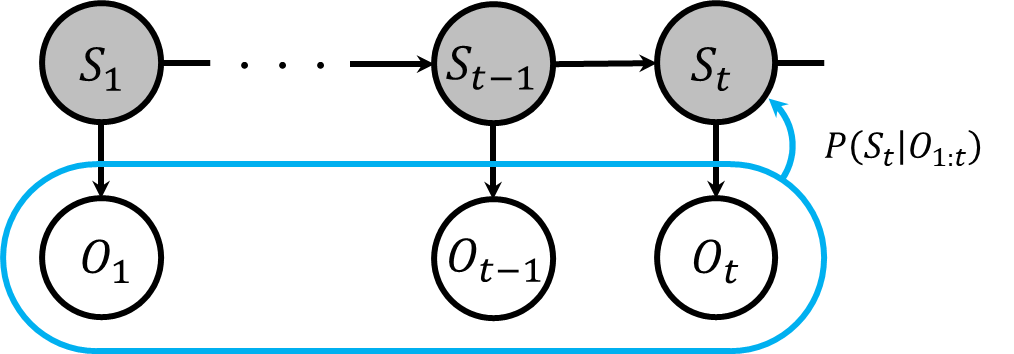
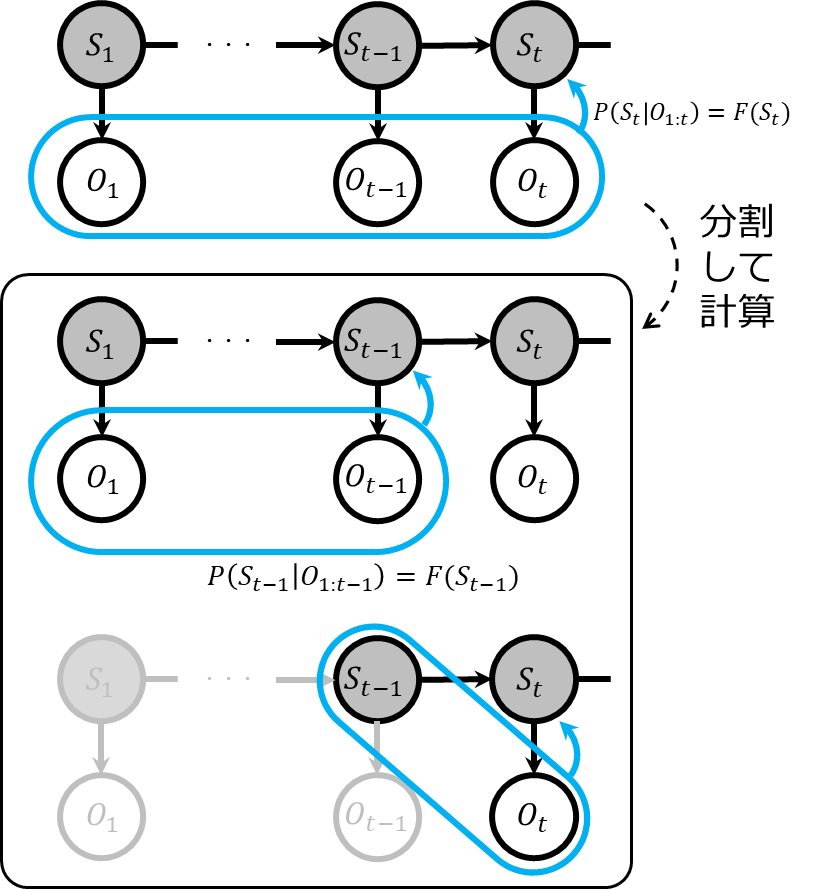
ここで、ベイズの定理を利用してこの計算を再帰的に行うことができます。具体的には、一つ前の時刻のフィルタリング結果\(F(S_{t-1})\)を使用して\(F(S_t)\)を求めます。式は以下の通りです。
$$\begin{eqnarray}
F(S_t) &=& P(S_t|O_{1:t}) \\
&\propto & P(O_t|S_t)\sum_{S_{t-1}}P(S_t|S_{t-1})P(S_{t-1}|O_{1:t-1})\\
&=& P(O_t|S_t)\sum_{S_{t-1}}P(S_t|S_{t-1})F(S_{t-1})
\end{eqnarray}$$
この式により、直前の時刻の状態推定値と現時刻の観測を使用して、現在の状態を推定することができます。このプロセスを各ステップごとに繰り返すことで、リアルタイムでの計算が可能となります。
部分観測マルコフ決定過程の状態推定
部分観測マルコフ決定過程の場合も、隠れマルコフモデルの状態推定と同じように考えることができます。
まず、部分観測マルコフ決定過程のフィルタリングでは、現在の時刻までに得られた観測データと行動データを基に、現在の時刻における状態を推定します。
式で示すと、以下のようになります。
$$
F(S_t) = P(S_t|O_{1:t}, A_{1:t-1})
$$
これは、以下のような式変形により再帰的に計算することができます。
$$\begin{eqnarray}
F(S_t) &=& P(S_t|O_{1:t}, A_{1:t-1}) \\
&\propto & P(O_t|S_t)\sum_{S_{t-1}}P(S_t|S_{t-1}, A_{t-1})P(S_{t-1}|O_{1:t-1}, A_{1:t-2})\\
&=& P(O_t|S_t)\sum_{S_{t-1}}P(S_t|S_{t-1}, A_{t-1})F(S_{t-1})
\end{eqnarray}$$
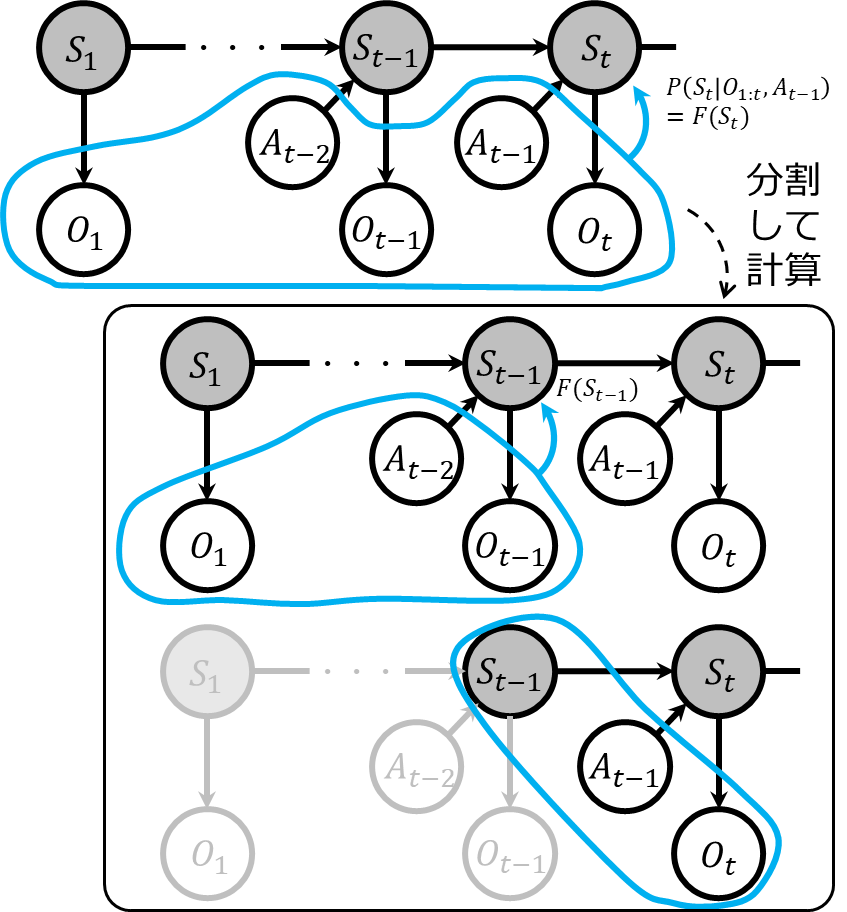
ベイズフィルタについては、ここで示した内容が基本となります。難しいと感じるかもしれませんが、実は特別複雑な操作を行っているわけではありません。どのようにして計算を行うのか、また、実際に計算が可能なのかと疑問に思う方もいるかもしれません。しかし、状態の遷移確率\(P(S_t|S_{t-1}, A_{t-1})\)や観測確率\(P(O_t|S_t)\)が既知であるという前提のもとでは、計算は可能です。次に、ベイズフィルタの状態推定をより具体的に理解してもらうために、自己位置推定問題について考えてみましょう。
ベイズフィルタによる自己位置推定
ベイズフィルタの理解を深めるために具体例として自己位置推定を見てみましょう。
自己位置推定の概要
自己位置推定とは何かというと、エージェントが自分自身の位置を特定するために必要なシステムです。これは自律移動ロボットがナビゲートする際に不可欠な技術とされています。
たとえば、下記のイラストのように9つのマスがあり、どのマスにいるのかを特定することが自己位置推定の一例です。実際には、この図のような部屋の単位での推定ではなく、もっと細かいミリ単位やセンチ単位での位置推定を行います。
自己位置推定にはいくつかの課題が存在します。例えば、ノイズを多く含むセンサーから得られる情報を元に、環境の変化に適応し、信頼性の高いデータを抽出する必要があります。ここでベイズフィルタを使用することになります。
その他の課題としては、非線形システムが非ガウスノイズに対応する場合などがあります。この動画では詳しく説明しませんが、ベイズフィルタベースの手法である粒子フィルタなどの手法でこれらの問題は解決可能です。

信念による自己位置の表現
信念とは、システムの現在の状態に関する確率分布を指します。この確率分布は「おそらくこうだろう」という確信の程度を示すものです。したがって、これを信念と見なすことができ、ベイズフィルターにおいては、推定された状態の確率分布を信念と称します。ベイズ更新は、典型的な信念更新のプロセスであり、初期分布(=初期信念)P(A)が外部情報によって事後分布(=新たな信念状態)P(A|B)へと更新されることを意味します。
自己位置推定における信念についてですが、自己位置はロボットが「恐らくここにいる」と確信する程度を表し、それを信念として扱うことができます。初期位置は事前分布(=初期信念)\(P(A)\)で示され、行動と観測に基づいて、移動後の位置(=事後信念)\(P(A|B)\)が求められます。
ベイズフィルタによる自己位置推定
自己位置推定に関する仮定として、地図情報、状態遷移確率(=環境ダイナミクス)、そして観測モデルが既知とします。
地図情報については、占有格子地図や点群地図などの表現方法があります。これらは私たちが普段使用している一般的な地図とは異なりますが、自己位置推定においてはこれらの表現方法がよく用いられます。
状態遷移確率\(P(S_{t+1}|S_t, A_t)\)とは、現在の状態\(S_t\)と行動\(A_t\)を基にした次の状態\(S_{t+1}\)への遷移確率であり、地図や環境の物理的特性に基づいたものです。例えば、滑りやすい地面では、80%の確率で意図した通りに移動でき、20%の確率で現在位置に留まる、といった具体的な確率を表します。
観測モデル\(P(O_t|S_t)\)は、ある特定の状態\(S_t\)で得られる観測データ\(O_t\)の生成確率を指します。これは、センサーの特性やノイズの影響を考慮したモデルです。

自己位置推定のプロセスを確率分布を使って具体的に考えてみましょう。下記にPOMDP(部分観測可能マルコフ決定過程)に基づく信念の更新プロセスで用いられる4つの主要な分布が示されています。まず、左上にあるのは更新前の信念分布です。これは、行動\(A_{t-1}\)を実施し、観測\(O_t\)を取得する前の状態\(S_{t-1}\)についての信念を示しています。右上の分布は行動\(A_{t-1}\)の結果として予測される信念分布であり、状態遷移確率を使用して移動の誤差を考慮した予測です。例えば、ロボットが1m前進する動作指示を受けた時、どの方向にどれだけ進むかを予測するということです。これは、我々が結果を知る前に予測を立てる一般的なプロセスに似ています。
次に、左下にある分布は尤度を示しています。これは、実際にセンサを通じて得られた観測から、ロボットがどこにいると判断されるかに関する情報です。最後に、右下の分布は更新後の信念分布であり、予測と尤度の情報を組み合わせて更新された信念です。予測と尤度が似ている場合は大きな更新はありませんが、もし予測と尤度に大きな差がある場合、これは予測誤差やセンサノイズなどを考慮して、より正確な位置情報に更新するための重要なプロセスです。つまり、このプロセスは予測のミスやセンサのノイズを相互に補正し合いながら、より正確な自己位置推定を行うために役立っています。
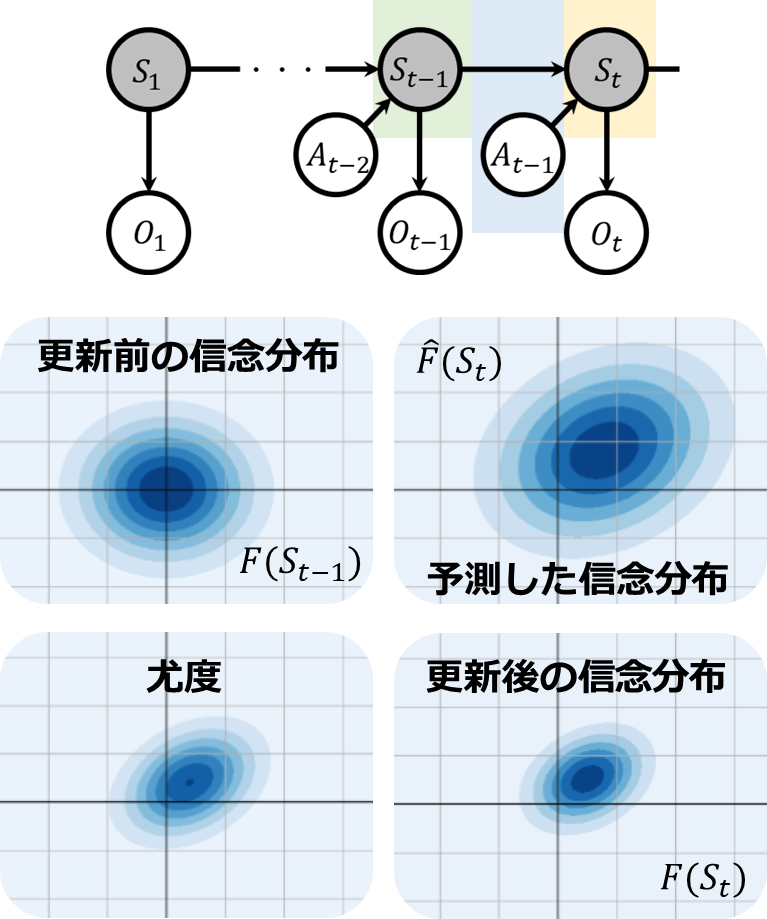
下図は、予測した信念と尤度の分布が異なる場合の例です。このように分布が異なっていても、融合した分布はノイズに大きな影響を受けにくいことがわかります。

ベイズフィルタの利点と欠点
ここまでの説明を踏まえると、ベイズフィルタの利点と欠点は次のようにまとめられます。ベイズフィルタの主な利点には、
- 不確実性の明示的な扱い:ベイズフィルタは不確実性を統計的に扱い、信念を確率分布で表現します。
- オンライン更新:データが入手されるたびに、即座に信念を更新できるため、動的な環境にも対応可能です。
- 柔軟性:異なるタイプのセンサーやモデルに容易に適用可能であり、多様な問題設定に対応できます。
一方、ベイズフィルタの欠点としては、
- モデルの複雑さ:正確なモデルを構築するには、システムの詳細な理解が必要になることがあります。
- 計算コスト:更新ステップにおいて膨大な計算量を必要とする場合があり、リアルタイム処理に制約が出ることがあります。
- スケーラビリティ:状態空間の次元が増加すると、計算コストやメモリ使用量が指数関数的に増大し、大規模な問題に対する適用が難しくなります。
といった点が挙げられます。これらの利点と欠点を考慮することで、ベイズフィルタを用いる場面を適切に選択し、問題解決に役立てることができます。
まとめ
本記事では、ベイズフィルタによる自己位置推定の基礎と応用について解説しました。ベイズフィルタは不確実性を統計的に扱い、データが入手されるたびに信念を更新することができる柔軟なフレームワークを提供します。これにより、動的な環境下でも高い精度の状態推定が可能になります。さらに、異なるタイプのセンサーやモデルに対しても適用可能であり、幅広い問題に対応できる柔軟性を有しています。
しかし、ベイズフィルタの使用にはいくつかの課題も存在します。特に、正確なモデルの構築が必要であり、そのためにはシステムの詳細な理解が求められます。また、更新ステップでの計算コストが高く、リアルタイム処理に制約が出る可能性があります。加えて、状態空間の次元が増加すると、計算コストやメモリ使用量が指数関数的に増大し、大規模な問題への適用が難しくなることも挙げられます。
余談として、ベイズフィルタを具体化した代表的な手法としてカルマンフィルタや粒子フィルタがあります。カルマンフィルタは線形システムとガウスノイズに最適化されたアプローチで、効率的な計算が可能ですが、非線形システムや非ガウスノイズには直接適用が難しいという制約があります。一方、粒子フィルタは非線形性や非ガウス性を持つ問題に対しても柔軟に対応できる利点がありますが、多数の粒子を使用することで計算コストが増大するデメリットがあります。これらのフィルタリング技術は、それぞれの長所と短所を理解し、適切な状況で選択・適用することが重要です。
これらの利点と欠点を総合的に考慮することで、ベイズフィルタを用いる場面を適切に選択し、問題解決に役立てることができます。ベイズフィルタの原理を理解し、その応用範囲を把握することで、さまざまな状況下での正確な状態推定が可能となり、自律移動ロボットのナビゲーションやその他多くの分野での応用が期待されます。
カルマンフィルタやベイズフィルタについては、別の記事で詳しく説明しているので、ぜひ、そちらもご覧ください。
カルマンフィルタや粒子フィルタについては以下の記事で解説しています。
最後までお読みいただきありがとうございました。