皆さんこんにちは。
この記事では、「【解説】ChatGPTでも使われるTransformerが賢い理由に迫る」というタイトルで、実はTransformerは非常に脳に似ており、ひょっとすると思考力を持っているのかもしれない、という話をしていきたいと思います(後半は私の妄想です)。
本記事のモチベーション
ではまず最初に、本記事のモチベーションについてお話ししたいと思います。つい先日、2024年3月27日に「The Topos of Transformer Networks」という論文がarXivに投稿され、それが少し話題になりました。この論文では、ChatGPTをはじめとして広く使用されているTransformerが、他のニューラルネットワーク、例えばMLPやCNN、RNNなどと比較して、表現力が圧倒的に豊かであることを数学的に証明しています。この記事ではその詳細を扱うわけではありませんが、この動画が投稿されたことをきっかけに、Transformerという高性能なアーキテクチャについてもう一度自分なりに考えてみたいと思った次第です。色々な論文を調査しながら考えた結果、Transformerは我々の脳にかなり似ているのではないかと感じましたので、この記事で扱いたいと思います。
Transformerのモチベーション
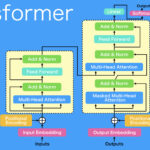
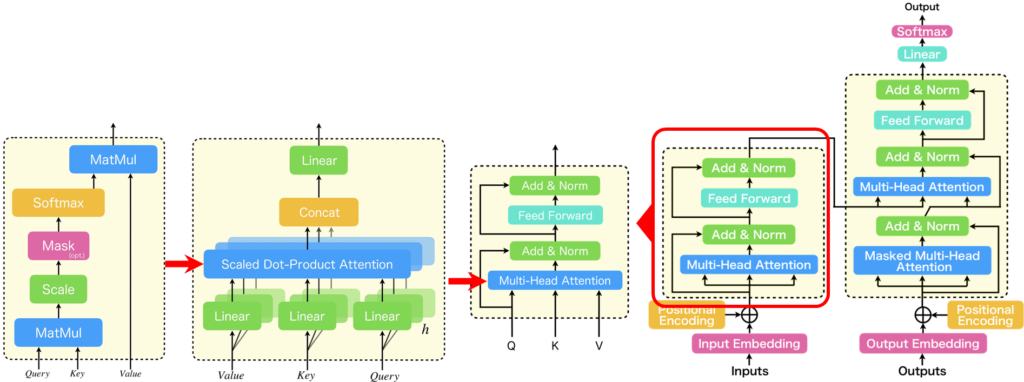
それではまず、Transformerの概要から説明していきます。Transformerは「Attention Is All You Need」と呼ばれる論文で提案された手法で、図に示すようなアーキテクチャをとっています。このTransformerは、従来の系列変換モデルが抱える位置依存性への弱さと、学習速度の遅さという課題に対処したものです。Transformerの基本ブロックは「Transformer Block」と呼ばれ、これが複数スタックされてエンコーダー・デコーダーモデルを構成しています。そして、このTransformerの「Multi-Head Attention」は、複数の「Scaled Dot-Product Attention」が並列に配置された構造をしています。この「Scaled Dot-Product Attention」は、図の1番左に示されるような構造となっており、Transformerにおいて非常に重要な役割を担っています。
Transformerについては以下の記事で詳しく解説しています。
Scaled Dot-Product Attention
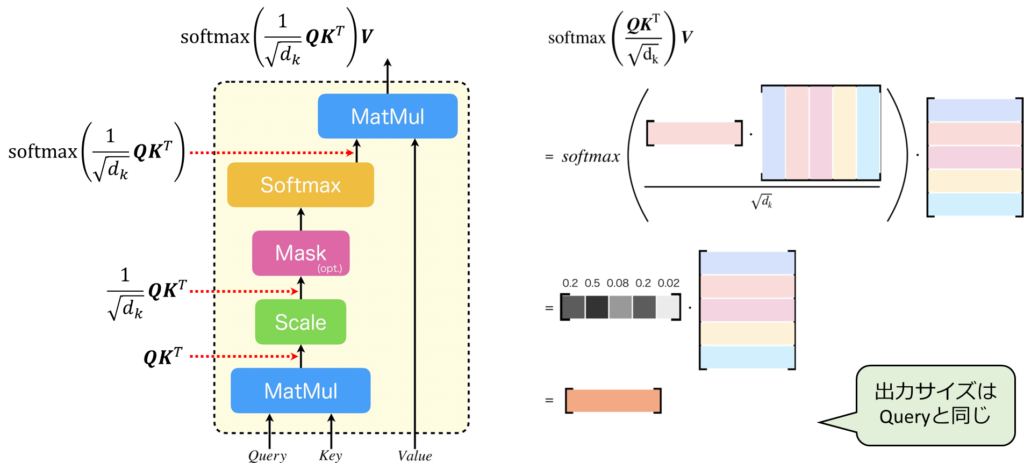
それでは、Scaled Dot-Product Attentionの式を見てみましょう。Scaled Dot-Product Attentionの入力には、「Query」、「Key」、「Value」の3つがあります。まず、左側の図を見てください。最初のMatMulでは、QueryとKeyが乗算されます。その後、\(\sqrt{d_k}\)でスケール化され、その結果にソフトマックス関数が適用されます。最後に、ソフトマックス関数が適用された行列とValueがMatMulによって掛け合わせられます。 次に右の図を見ながら実際にトークンベクトルをイメージしながら、どのように処理が行われるのかを見てみましょう。ある単語のトークンベクトルが図のような行ベクトルで表されると仮定します。この例で、Qはこの1個のトークンベクトルです。Kについては、トークンベクトルが5つ並べられた行列で、それが転置されています。VについてはKと同じです。つまり、これはSourceTarget Attentionです。この時、ソフトマックスの内部では、提供されたQueryとKeyとして与えられた行列の各トークンに対して内積が行われます。そして、\(\sqrt{d_k}\)でスケール化された後にソフトマックス関数が適用されると、すべての合計が1になるような行ベクトルが生成されます。その行ベクトルとバリューが掛け合わされ、新しいベクトルが計算されます。ここでの出力サイズはクエリーと同じです。Scaled Dot-Product Attentionでは、このような計算が行われます。
詳細は以下の記事で解説していますのでもしよければ、そちらをご参照下さい。
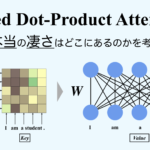
Scaled Dot-Product Attentionには、学習によってチューニングされる重み要素が存在しないという点が非常に興味深いです。下図をご覧ください。ここでは、QueryとKeyを入力とし、ソフトマックスを適用するまでの処理を行います。図の左側には、QueryとKeyを用いて計算された行列\(\boldsymbol{W}\)が示されています。そして最後のMatMulは、行列\(\boldsymbol{W}\)を重みとして用い、Valueを入力とする密結合層と解釈できます。ここで、行列\(\boldsymbol{W}\)はQueryとKeyの内積によって決まるため、入力によって動的に変化することになります。つまり、Scaled Dot-Product Attentionは学習によりチューニングされる重みは持たない一方で、入力に依存して動的に変化する重みをもつ密結合層として機能します。通常、ニューラルネットワークは学習時に重みをチューニングし、その後は重みを変更しないことが一般的ですが、このScaled Dot-Product Attentionは異なります。入力パターンが無限にある場合、この行列のパターンも実質的に無限になるため、表現力が非常に高いと言えます。
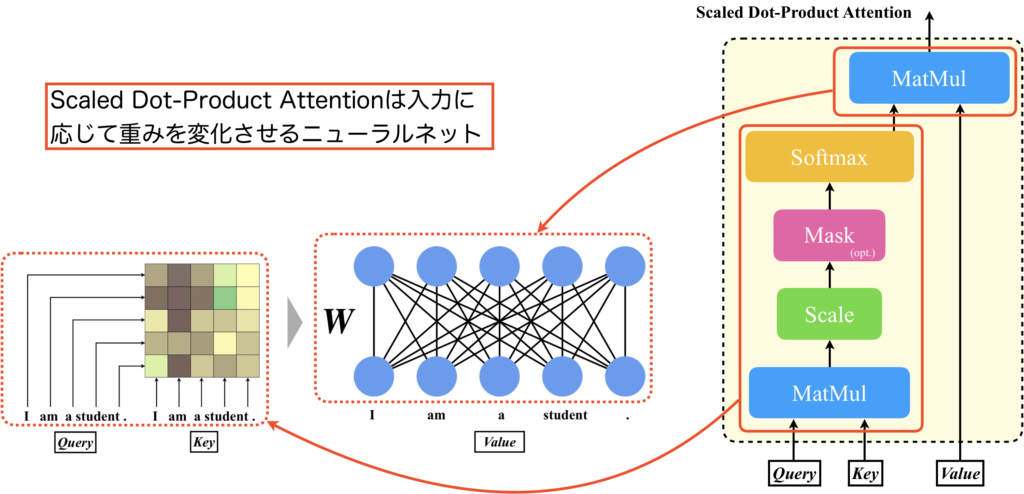
Transformerを構成する各層の重みの性質
ここで、Transformerを構成する密結合層の重みの性質について簡単に確認しておきましょう。下図の右にはTransformer Blockが、真ん中にはMulti-Head Attentionを拡大したものが記載されています。
赤で囲った部分がScaled Dot-Product Attentionで、先ほど説明した通り、重みが入力系列によって動的に変化する部分です。Transformerにはそれ以外にも多くの密結合層があります。具体的には、Scaled Dot-Product Attentionの直前のLinear層、それらをconcatした後のLinear層、そしてFeed Forward層です(青で囲った部分)。これらの層は学習時以外では重みが変化しません。
RNNやCNNなど、従来の系列処理モデルは学習時以外は重みが固定されている層のみで構成されていましたが、Transformerは入力によって重みが動的に変わる層が含まれる構造になっているため非常に革新的だと考えられます。
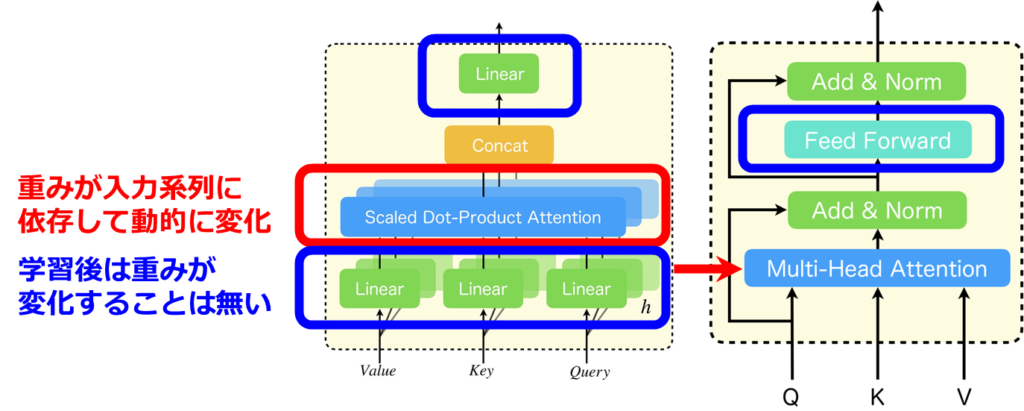
海馬と連想記憶モデル
それでは、次に海馬と連想記憶のモデルについて説明をしていきます。
大脳辺縁系と海馬
まず、基礎知識として大脳辺縁系と海馬について簡単に説明します。大脳辺縁系は、海馬、偏桃体、帯状回といった複数の構造から成り立っています。このシステムは基本的な感情の処理やストレス反応、記憶の形成と保存、長期記憶への転送など非常に重要な役割を果たしています。その中でも海馬は、短期記憶を長期記憶へと変換するプロセスに不可欠であり、適切に記憶を保持するなど思考に大きく関与しています。
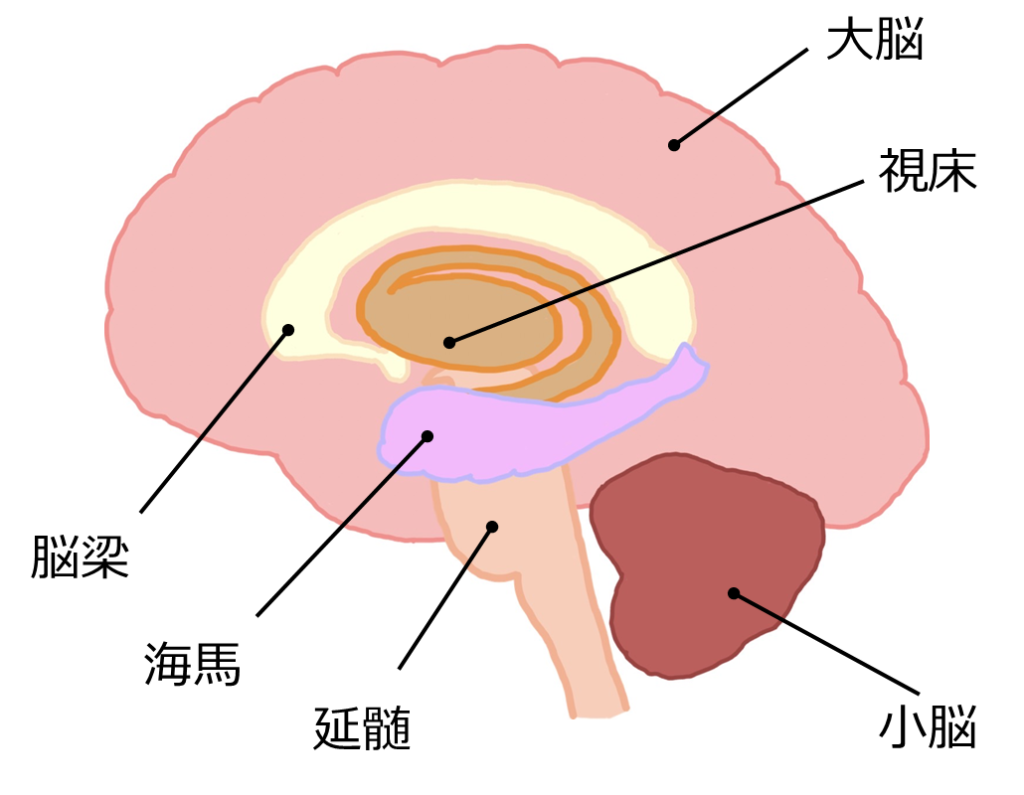
海馬の内部構造と数理モデル
では、海馬の内部構造と数理モデルについて説明します。海馬はCA1、CA2、CA3と呼ばれる領域に分けられており、それぞれが特有の機能と神経回路を持っています。CA1については、主に他の脳領域からの情報を受け取り、そして送り出すという操作を行っています。CA2は社会的記憶や行動に特に関与していると考えられています。CA3については、パターンの検出や記憶の再生、つまり連想記憶に強く関与しているとされており、下図の右に示すような相互結合ネットワークが見られます。
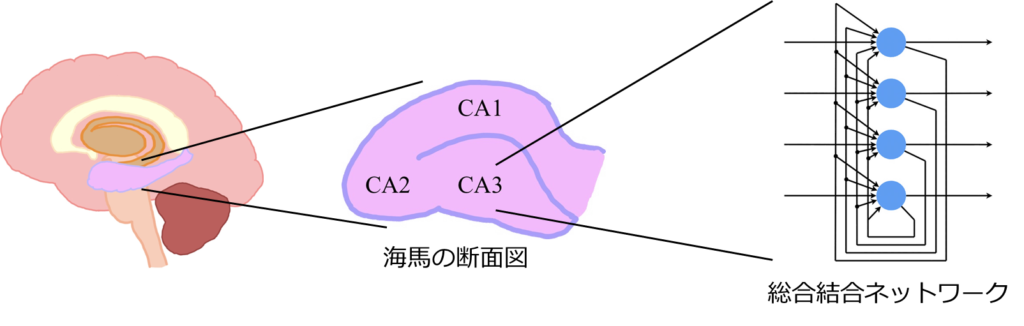
連想記憶モデルのHopfield Network
この相互結合型のネットワークは連想記憶のモデルとして重宝されており、その連想記憶のモデルの代表的なものにHopfield Networkがあります。ここでは簡単にHopfield Networkについて説明します。Hopfield Networkとは、下図右に示すように各々のニューロンが相互に結合する構造となっており、情報をネットワークの状態として記憶します。初期のHopfield Networkでは、結合の重みはヘブの法則を用いて決定します。このHopfield Networkで情報を思い出す、つまり想起する際には、初期状態から徐々にエネルギー関数の値が小さくなるようにネットワークの状態を更新していきます。このエネルギー関数において極小となっている部分がネットワークが記憶している状態です。ですから、どこから始まってもいずれどこかの極小値に到達し、何かしらを思い出すわけです。
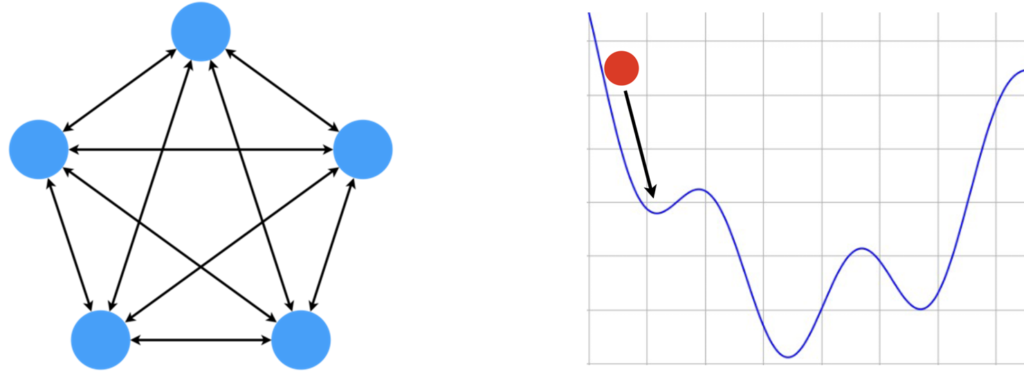
それでは、Hopfield Networkの具体的な使い方について簡単に説明します。ここでは、Hopfield Networkにリンゴの画像を覚えさせたとします。ここで、学習後のHopfield Networkに、一部が欠け画像を入力することを考えます。このように不完全な画像が与えられたとしても、Hopfield Networkは状態を更新するにつれて、欠けている部分を徐々に思い出すことができます。そして、最終的に極小値に到達したところで完全なリンゴの画像を思い出します。ここに示したイラストは、分かりやすくするために最初に覚えさせたリンゴの画像の一部を欠かせた画像を入力していますが、実際にはもっと異なる画像を入力しても適切に思い出すことができます。
Modern Hopfield Network
ただし、Hopfield Networkには記憶容量が少ないということや、別の記憶を誤って想起してしまったり、記憶同士が衝突して、最初に記憶させた記憶には存在しないはずの記憶が誤って引き出されてしまうという現象がありました。そのため、2020年に『Hopfield Network is All You Need』という新しい論文でModern Hopfield Networkが提案されました。
このModern Hopfield Networkは、従来のHopfield Networkの記憶容量の少なさを主に改善したもので、新しいエネルギー関数と更新ルールを提供することにより、指数関数的な膨大な記憶容量を実現しています。以降の話では、Modern Hopfield Networkが非常に重要な要素となってきます。
連想記憶モデルとAttention
それでは、連想記憶モデルとAttentionについてその関係を説明していきます。Hopfield Network is All You Needでは、Modern Hopfield NetworkとScaled Dot-Product Attentionの計算式が非常に似ているということが紹介されています。
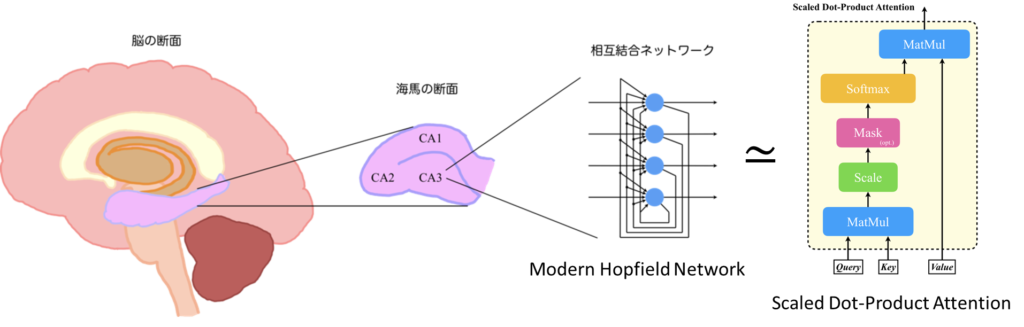
Modern Hopfield NetworkとScaled Dot-Product Attention
これはどういうことかと言うと、Modern Hopfield Networkの更新式からAttentionが導出できるということです。
本記事では、Modern Hopfield Networkの更新式からScaled Dot-Product Attentionの計算式を導出してみましょう。
まず、Modern Hopfield Networkの更新式は次のように表現されます。
$$
\boldsymbol{\xi}^{new} = \boldsymbol{X}\text{softmax}(\beta \boldsymbol{X}^T \boldsymbol{\xi})
$$
ここで\( \boldsymbol{X}\)とはベクトルで表された記憶パターンを複数並べて行列にしたもので、 \(\boldsymbol{\xi}\)はニューロンの状態を表すベクトルとなっています。ではModern Hopfield Networkの更新式の文字を置き換えていきたいと思います。まず、\( \boldsymbol{\xi}\)を\( \boldsymbol{Q}^T\)に、\( \boldsymbol{X}\)を\( \boldsymbol{K}^T\)に、\( \boldsymbol{\beta}\)を\( \sqrt{d_k}\)に置き換えると、このように表すことができます。
$$
(\boldsymbol{Q}^{new})^T = \boldsymbol{K}^T\text{softmax}\left(\frac{1}{\sqrt{d_k}}\boldsymbol{KQ}^T\right)
$$
そして、この式全体を転置すると、次のように書き換えることができます。
$$
\boldsymbol{Q}^{new} = \text{softmax}\left(\frac{1}{\sqrt{d_k}}\boldsymbol{QK}^T\right)\boldsymbol{K}
$$
ここで、最も右端の\(\boldsymbol{K}\)を\(\boldsymbol{V}\)に、そして新しい\(\boldsymbol{Q}\)(\(=\boldsymbol{Q}^{new}\))を\(\boldsymbol{Z}\)に書き換えると、Scaled Dot-Product Attentionの式になります。
$$
\boldsymbol{Z} = \text{softmax}\left(\frac{1}{\sqrt{d_k}}\boldsymbol{QK}^T\right)\boldsymbol{Z}
$$
ただし、ここでは説明を簡略化するために厳密性に欠ける式変形をしている点はご了承ください。そのため、正確な式変形を知りたい方は原論文をご参照ください。
ひとまず、Modern Hopfield Networkの更新式とScaled Dot-Product Attentionの計算式が類似(使い方によっては全く同じになる)していることをご理解いただけると思います。
Hopfield Networkは先ほど説明した通り、海馬のCA3のモデルとなっていますから、要するにここではScaled Dot-Product Attentionは海馬のCA3の役割を果たしていると解釈することができるのではないでしょうか。
Transformerは脳に似ているかも
それでは、Transformerが脳に似ているという話をしていきます。ここからは私の妄想がかなり入ってくるため、話半分で聞いていただければと思います。Transformerを構成する基本ブロックである「Transformer Block」は、海馬と大脳を持つとても脳に似た構造をしているのではないかと思っています。下図に示すように、Transformer Blockを、複数のScaled Dot-Product Attentionが並列になって構成された「Multi-Head Attention」を海馬に見立て、その後に続くFeed Forwardを大脳に見立てました。
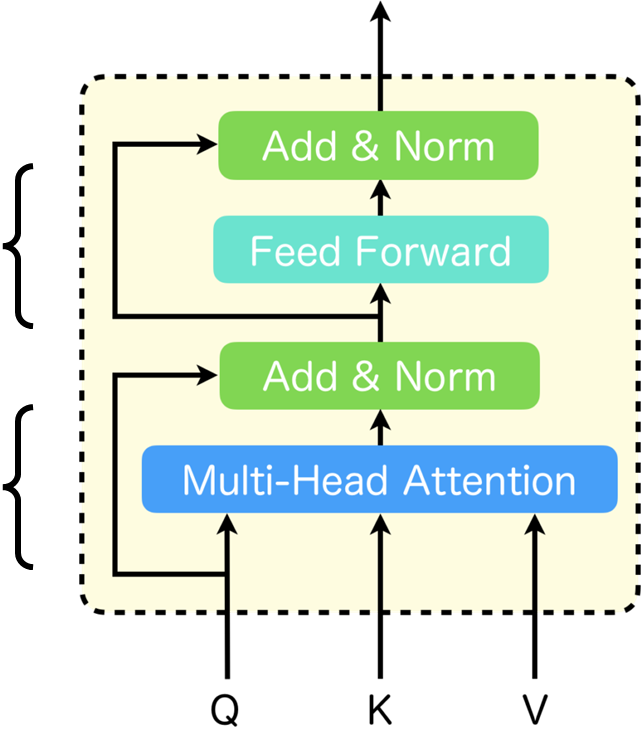
このFeed Forwardの部分が大脳なのか小脳なのか、大脳辺縁系なのか、または海馬の一部なのかについては特に意見が分かれると想像しますが、海馬は大脳と非常に密接に接続されているので、ここでは大脳としています。そして、TransformerではこのTransformer Blockが複数スタックされるわけですから、Multi-Head Attentionで連想した記憶をFeed Forwardで処理し、次の層のMulti-Head Attentionで更に連想するという処理を行います。
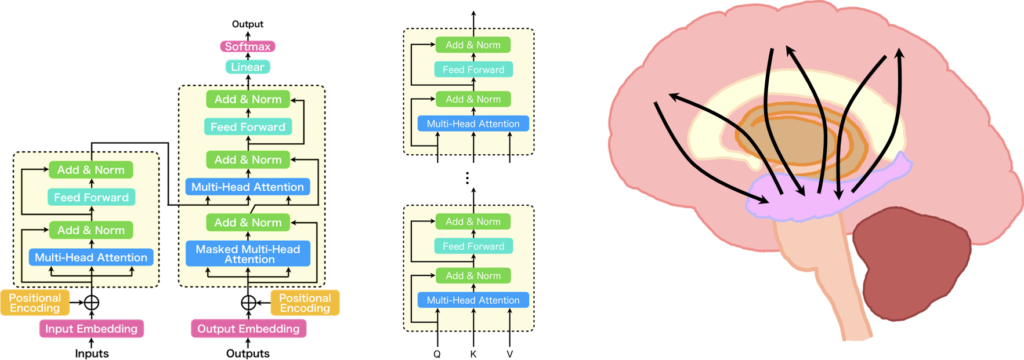
ですから、Transformerは海馬と大脳の間で行っている情報処理に近い処理を行っているという解釈ができるかもしれません。そうなると、Transformerはひょっとすると思考ができるのかもしれません。
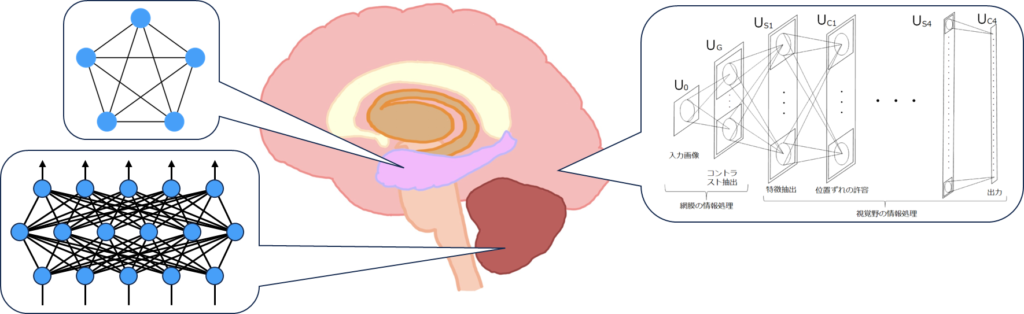
これまで、たとえば視覚野をモデル化したネオコグニトロンがCNNの提案につながったり、小脳が多層パーセプトロンの可能性を持つとされたことがあります。これらは脳の局所的なネットワーク構造の再現に留まっていましたが、Transformerは海馬として機能するAttentionメカニズムを取り入れることで連想する能力を獲得しました。MLPやCNNのような従来のニューラルネットワークは、入力に対する出力を単に対応付けて学習するだけでした。例えば、ある画像が入力された場合、それが何であるかを識別するCNNは、画像に対するラベルを学習するだけで、連想機能は持っていませんでした。また、時系列を扱うRNN、特にLSTMにはCECセルという記憶セルが含まれ、これは一見海馬と類似していますが、CECセルは単なる記憶機能に過ぎず、連想する力はありませんでした。しかし、Transformerは連想する力を持っており、私たちが思考する上で重要な連想が可能です。このため、Transformerが思考している可能性があります(思考の定義にはよると思いますが)。
では、改めてTransformerと従来のモデルとの違いを考えてみましょう。従来のニューラルネットワークは単なる丸暗記型ですが、Transformerは考えながら理解するタイプです。つまり、Transformerは連想プロセスを通じて知識を学習します。従来の系列モデルが文章をトークン列として扱っていたのに対し、Transformerは文章の全体像を状態として一度に捉えて入力するため、文章の状態を連想し、未知の文章にも柔軟に対応できると考えられます。これは丸暗記型ではないからこそ実現できることです。もう一度言いますが、Transformerは思考しているのかもしれません。
さいごに
本記事には、Transformerが従来型のニューラルネットワークに比べて、その表現力が圧倒的に豊かであることが数学的に証明されたことを切っ掛けに、私なりにTransformerについて考えたことを記載しました。Attention機構は会話の流れを理解し、文章全体を一つの状態として捉え、連想を通じて記憶から適切な知識を引き出すのに重要な役割を果たしていると考えられます。Transformerの構造は、海馬と大脳を持つ脳構造に似ており、これにより思考が必要な複雑な処理にも適応できるのかもしれません。
以上で本記事の内容は以上です。後までお読みいただきありがとうございました。