Transformer[1]の核心となる仕組みであるAttentionは、入力シーケンス内の各トークン間の関連性に基づいて注意の計算を行います。それにより、Transformerは従来の系列処理において主流であったRNNの性能を凌駕する性能を実現し、更には画像処理などの領域でも大きな成果を上げることができました[2]。このように従来のモデルでは成し得なかったような成果を達成できる万能な仕組みであるAttentionですが、その計算コストは入力シーケンス長\(n\)に対して指数関数的に増加するという大きな課題を持ちます。つまり、扱えるシーケンスの長さは計算機のハードウェア性能に大きく影響され、ある程度のシーケンス長を扱うには、高い処理能力と大容量のメモリを持つ計算機が必要となります。そのため、如何にすればAttentionの計算コストを下げることができるのか、計算量を減少させられるかが研究されています。様々なアプローチで研究がされていますが、本記事で紹介するのは、Attentionの計算をスパースにするという手法である、Sparse Attention[3]について紹介します。Sparse Attentionは本記事の執筆時点(2023年)でも利用されている重要な手法です。本記事を通じて、Sparse Attentionのエッセンスについてご理解いただければ幸いです。
本記事の構成について説明します。前半部分では、Sparse Attentionを理解するために必要な基礎知識を説明します。具体的には、2017年に発表されたTransformerや、Attention、Attention Matrixについて、図や数式を用いて詳しく説明します。後半は、本記事の本題であるSparse Attentionについて詳しく説明します。
前提知識
まず、前提知識としてTransformer、Attention、Attention Matrixについて説明します。Transformerについては、Attentionをはじめて一般化しそれを中心に添えたモデルとなっており、Attentionを知るうえで欠かすことのできないアーキテクチャです。そして、Transformerで使用されたAttentionはその後の改良型Attentionの基礎となり、特にSparse AttentionはAttention Matrixと密接に関連しています。それらについて順番に説明します。
Transformer
Transformerは、2017年に発表された「Attention is All You Need」[1]という論文にて提案された機械翻訳モデルです。Transformerは下図に示すように、Seq2Seqをベースとしたモデル構造をしています。
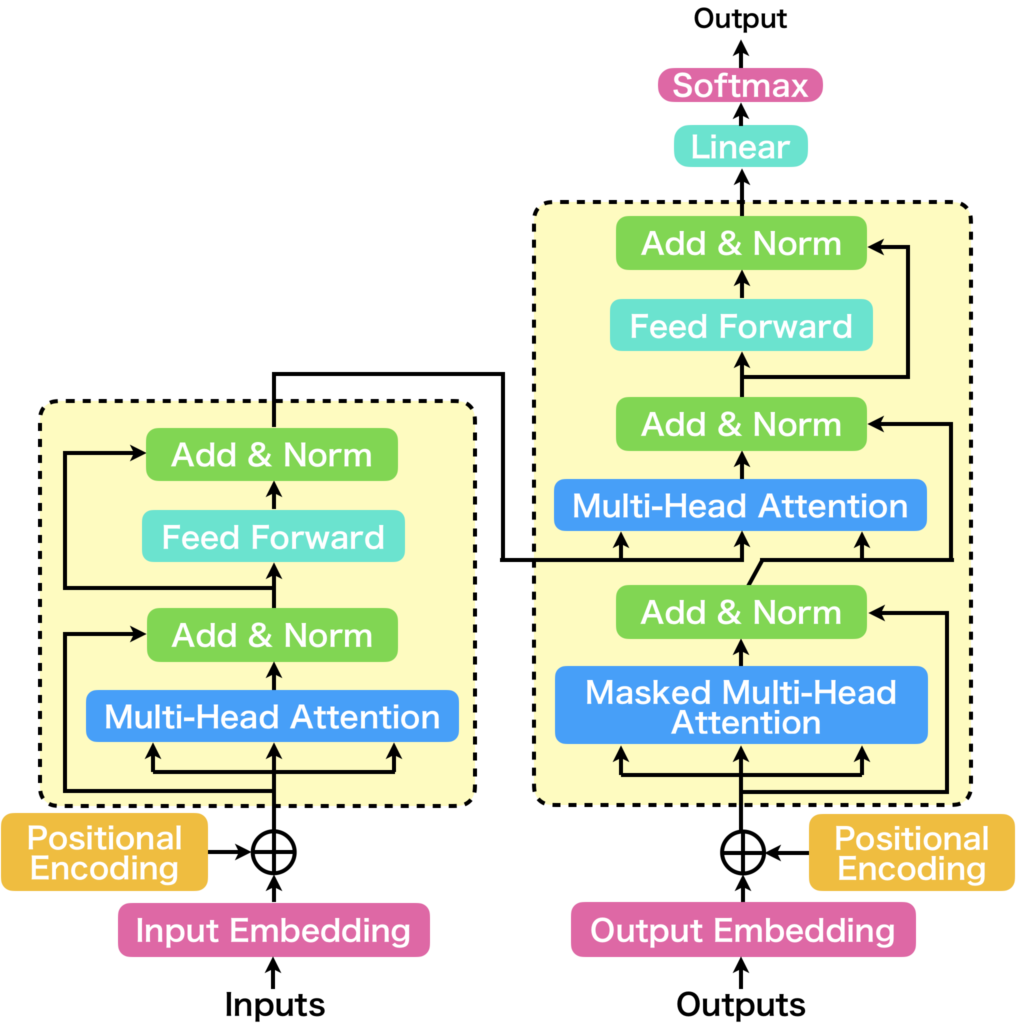
現在は、自然言語処理の枠を超えた多種多様な領域において大きな成果をあげています。Transformerの主な構成要素は以下の3つです。
- Positional Encoding
- Multi-Head Attention
- Position-wise Feed Forward
Positional Encodingは、Transformerに入力された各トークンの系列情報に位置情報を表すベクトルを加えます。Transformerは系列モデルとはいえ、RNNのように過去の情報を記憶するような記憶機構は持たないため、Positional Encodingが無い場合、系列情報内の時間的な流れをとらえることが難しくなります。
Multi-Head Attentionは、単一のAttention(Scaled Dot-Product Attention)の入力に線形層を追加した構造(Single-Head Attention)を複数並列化することで、多様な注意情報を取得できるように設計されています。Scaled Dot-Product Attentionとは、簡単に説明すると入力された系列情報間の各トークンベクトル間で内積を計算し、それに基づいて内積の大きいワードに多くの注意を向けて線形結合することで次のベクトルを生成する仕組みです。詳しい内容は次に説明します。
Position-wise Feed Forwardは、Multi-Head Attentionの出力を各トークンごとに変換するネットワークです。トークン毎にという点が重要で、それがPosition-wiseの意味になります。使用されているニューラルネットワークは単純な3層型です。
ここまでTransformerの主な構成要素について簡単に説明してきました。Transformerが開発された背景事情など、本記事では説明していない内容に興味のある方は以下の記事を参考にしていただければと思います。
Attention(Scaled Dot-Product Attention)
Transformerで使われているAttentionの最小単位のScaled Dot-Product Attentionについて説明していきますが、その前に、Scaled Dot-Product Attentionが、どこにどう使われているかを下図に示しましたので、Scaled Dot-Product Attentionの説明に入る前に簡単に紹介します。
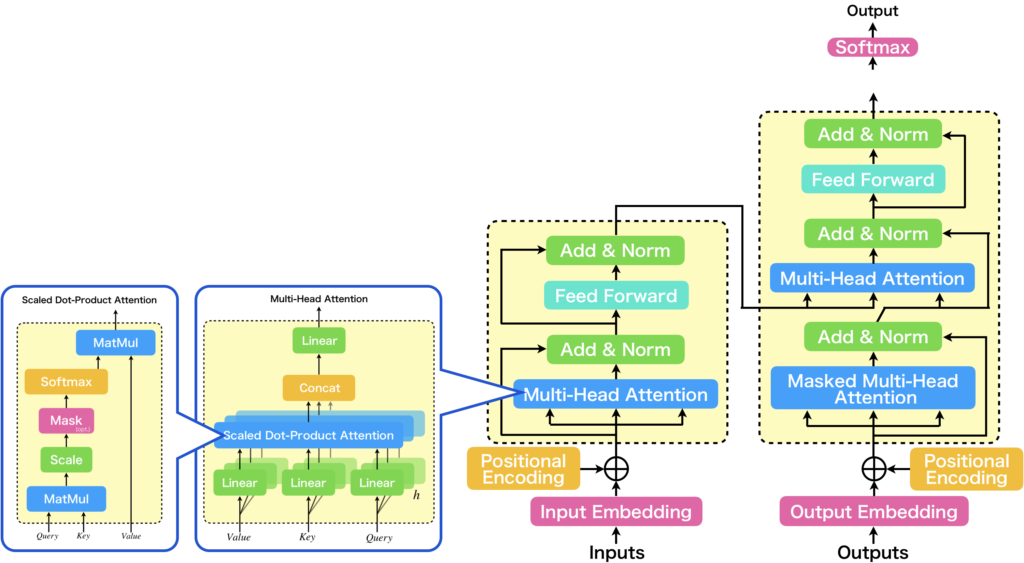
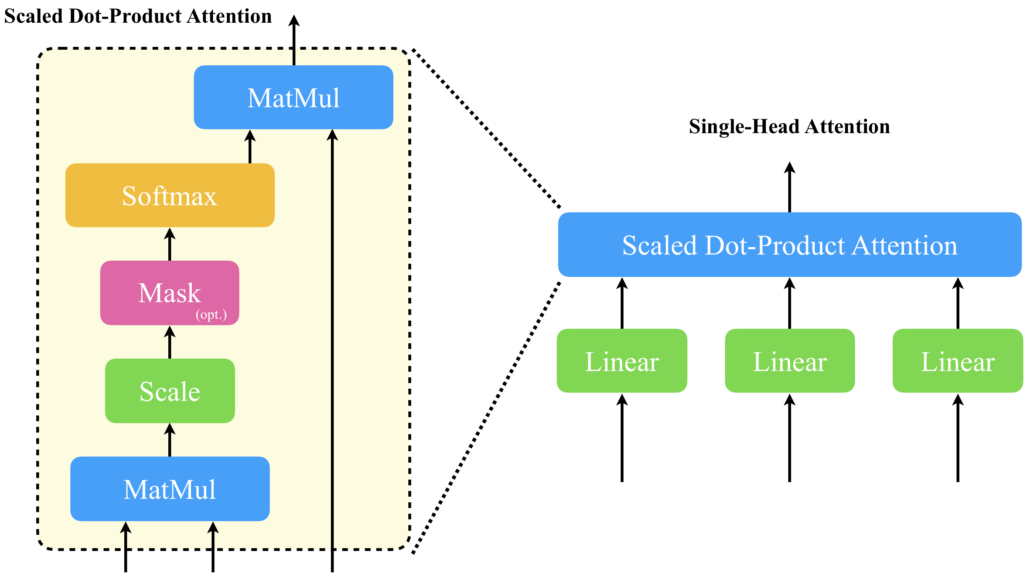
右側に、先ほど示したTransformerモデルが記載されています。Transformerの主な構成要素の1つとして紹介した、Multi-Head Attentionに注目した図が中心から少し左に記載されています。Multi-Head Attentionは、Scaled Dot-Product Attention(図中左)の入力に線形層を付与したSingle-Head Attentionを複数並列に並べ、それらの出力をconcatとLinear層でフュージョンする構造をしています。Scaled Dot-Product Attentionを単に並列化するだけでは不十分な理由は、Scaled Dot-Product Attentionが入力シーケンスの各トークン間で内積を計算するだけで、それ自体に学習パラメータが存在しないからです。これが何を意味するかというと、Scaled Dot-Product Attentionだけを複数並列化したところで、それぞれからの出力は全て同じであり、表現可能な注意表現を増やすことに寄与しないということです。表現可能な注意表現にバリエーションを持たせるには、並列に並べられた各々のScaled Dot-Product Attentionに入力されるベクトルを違うものにする必要があります。そこで使用されているのが、Linear層です。Linear層は活性化関数を持たない、もしくは活性化関数が恒等関数の層と考えることができ、これをScaled Dot-Product Attentionの入力の直前に追加することで、多種多様な注意表現を表現することが可能になります。これが、Multi-Head Attentionです。Multi-Head Attentionについて更に詳しい内容を知りたい方は、以下の記事をお読みいただければと思います。
では、Scaled Dot-Product Attentionの計算について説明します。Scaled Dot-Product Attentionの入力は、(\(Q\))、キー(\(K\))、値(\(V\))の3つで、これらの成分を用いて注意を計算します。具体的には、クエリと各キーの間の内積を計算し、その結果をスケーリング(通常は次元の平方根で除算)します。これにより、各キーとクエリの間の適合度が計算されます。次に、これらのスケーリングされた適合度をソフトマックス関数に通すことで、確率的な重み(すなわち、注目度)を得ます。最後に、これらの重みを値に適用(通常は重みの和で)することで、最終的な出力を得ます。
このメカニズムは、ネットワークがクエリに最も関連性の高い情報(値)に「注目」する能力を提供します。また、スケーリングは、ドット積が非常に大きくなることによるソフトマックス関数の勾配消失問題を緩和します。
以下に、Scaled Dot-Product Attentionの計算の概要を示します:
- クエリ(\(Q\))とキー(\(K\))のドット積を計算します:\(QK^T\)
- スケーリングを行います:\(QK^T / sqrt(d_k)\) (ここで、\(d_k\)はキーの次元数)
- ソフトマックス関数を適用して確率的な重みを得ます:\(softmax(QK^T / sqrt(d_k))\)
- これらの重みを値(\(V\))に適用します:\(softmax(QK^T / sqrt(d_k))V\)
この計算は、各クエリに対して行われ、結果として注目度によって重み付けされた値の集合が得られます。これが、Scaled Dot-Product Attentionの出力となります。
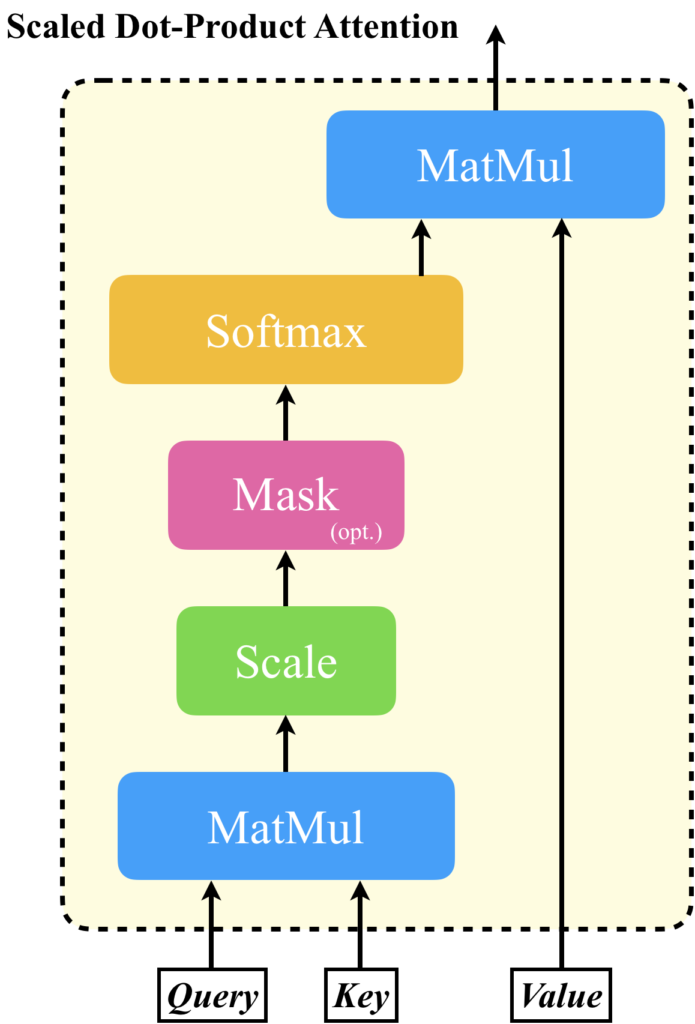
ベクトルや行列の形を考えてみるとイメージしやすいでしょう。入力されるトークンベクトルを行ベクトルとし、それらが縦方向に並べられた行列によりシーケンスデータが表現されているとします。これを、KeyとValueに与えるとします。Queryにも同じ行列を与えることができますが、ここでは説明の都合上、任意のトークンベクトルを1つだけ与えることを考えます。すると、Scaled Dot-Product Attentionの計算によるベクトルや行列の変化は以下の図のようになります。簡単に説明すると、Queryとして与えられたトークンベクトルと、Keyに与えられたシーケンスの各トークンベクトルと内積を計算し、どのトークンとの関連度が近いか計算し、それに基づいてValueのトークンベクトルを線形結合することで、Queryに対する出力ベクトルを計算します。
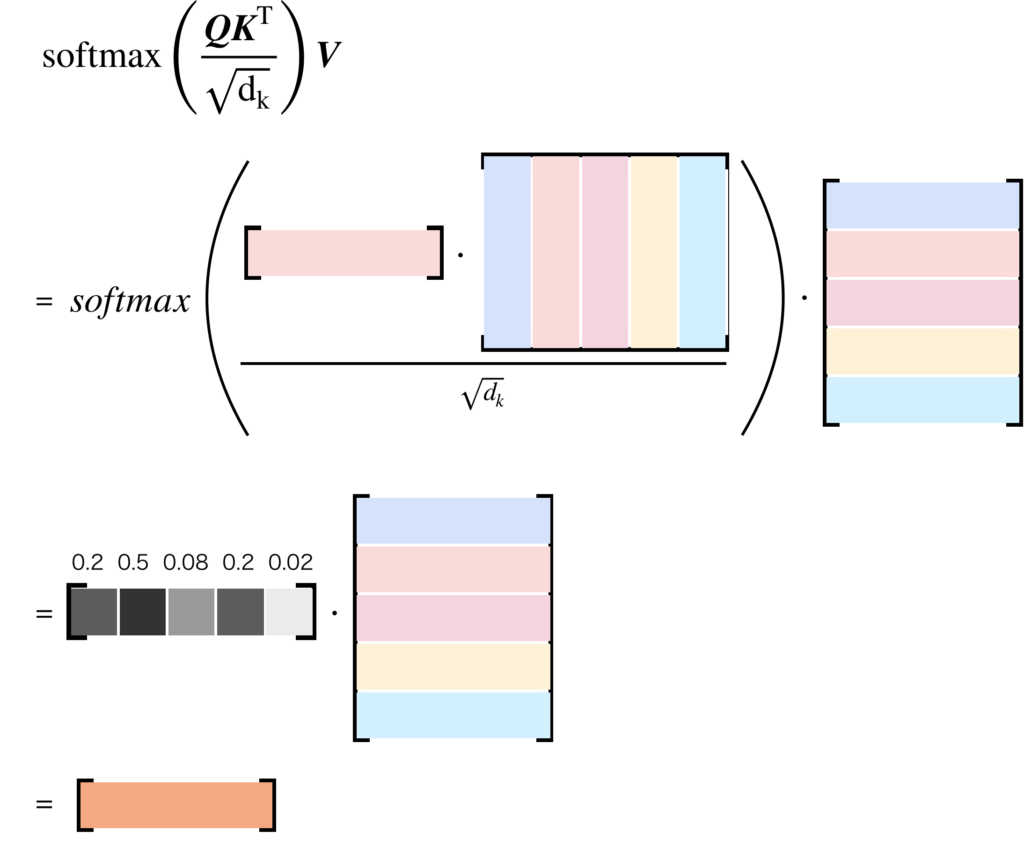
Scaled Dot-Product Attentionの処理を理解していただけたところで、この仕組みのどこが原因で、入力シーケンス長に対して2乗のオーダで計算コストが増加してしまうのだと思いますか?
その原因は、Scaled Dot-Product AttentionにおけるQueryとKeyの内積を計算するMutMul操作にあります。
Linear層の計算コストはあまり問題にならないのか、という疑問が生じるかもしれません。結論から言うと、Scaled Dot-Product AttentionのQueryとKeyの内積を行うMutMulのようには問題になりません。Linear層は入力された各々のトークンベクトルに対して適用されます。シーケンス長が \(n\)から\(2n\)になることで増える計算コストは2倍です。つまり、計算量は\(O(n)\)です。
Attention Matrix
Scaled Dot-Product AttentionのQueryとKeyの内積を行うMutMulで生成された行列は、スケール処理、マスク処理、softmax関数の適用が行われます。この行列を、Attention Matrixといいます。入力シーケンス長に応じてAttentionの計算コストが2乗のオーダーで増加するのは、Attention Matrixの成分数が入力シーケンス長に対して2乗で増加するからです。
では、Attention Matrixについて具体的に見ていきましょう。以降では入力シーケンスは、自然言語による文章をトークン化して並べた行列とします。この行列を、Scaled Dot-Product AttentionのQuery、Key、Valueに入力すると、Attention Matrix(下図左)はクエリとキーの間のスケーリング&softmaxが適用された行列を表します。具体的には、行列の各要素は、対応するクエリとキーの間の関連性(または「適合度」)を表します。
デコーダの場合、未来の情報に対する「注目」を防ぐために、マスクが必要となります。具体的には、Attention Matrixの特定の要素を無限大の負の値(通常は-∞)に設定することで、ソフトマックス関数がこれらの要素に対してゼロの重みを割り当てるようにします。これにより、デコーダは自身の未来の出力に「注目」することができなくなります。
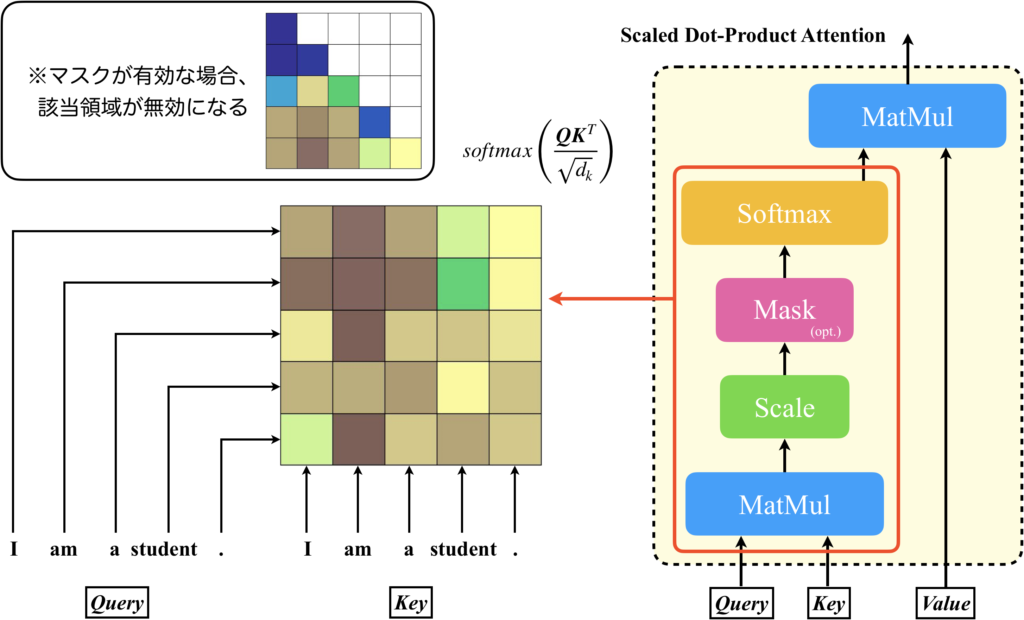
このAttention Matrixは、Single-Head AttentionやMulti-Head Attentionのように入力に線形層を追加してもサイズは変わりません。線形層によりトークンベクトルの次元数が小さくなったとしても、そのベクトルが並ぶ数はシーケンス長に依存するからです。線形層を追加するメリットは、Attention Matrixのバリエーションを増やすことができることです。
下図は、線形層を追加することでAttention Matrixが変化することを表しています。
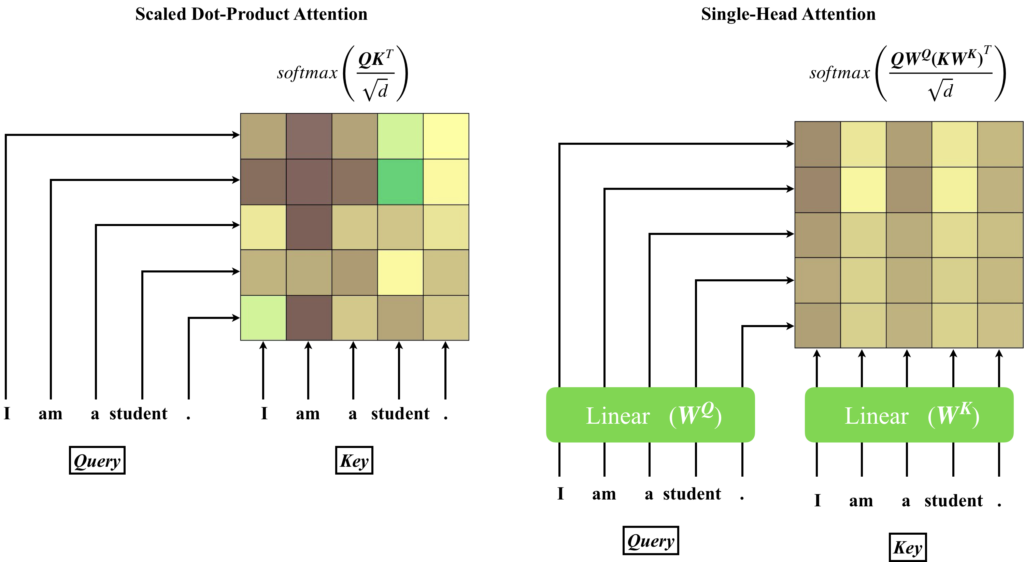
以上が、Attention Matrixの説明です。
Sparse Attention
Sparse Attentionとは
さて、本題のSparse Attentionの説明をしていきます。Attention Matrixは、入力テキストの各単語(またはトークン)が他のすべての単語とどの程度関連しているかを示すため、入力テキストの長さに応じて二乗で大きくなります。
入力シーケンスが\(n\)個のトークンからなる場合、Attention Matrixは\(n × n\)のサイズとなり、長いテキストを扱う際に計算量とメモリ使用量が大きくなるという問題を引き起こします。そのため、長いシーケンスを効率的に処理するための様々な手法が提案されており、今から説明するSparse Attentionもその1つです。
Sparse Attentionは、Attention MatrixをスパースにすることでAttentionの計算の効率化を実現する手法です。スパースな行列に関する研究は様々行われており、スパース性を活用すれば計算効率化やメモリ削減を達成できる可能性を秘めています。Sparse Attentionは、スパース化の恩恵を享受したものになります。では、Sparse Attentionというのは、いったいどのような計算で実現され、どのような種類があるのでしょうか。順に説明していきます。
Sparse Attentionの数式表現
Scaled Dot-Product Attentionの数式をもう一度示します。
$$
Softmax\left(\frac{QK^T}{\sqrt{d_k}}\right)V
$$
ここでAttention Matrixは、数式中の\(Softmax\left(\frac{QK^T}{\sqrt{d_k}}\right)\)ですので、\(A=Softmax\left(\frac{QK^T}{\sqrt{d_k}}\right)\)と置くと、Attentionの出力は\(AV\)になります。ここで、正規化とソフトマックス関数を適用する前のAttention Matrixを\(\hat{A}\)と置いたとき、Sparse Attentionは以下のような式で表されます[4]。
$$
\boldsymbol{\hat{A}_{ij}} = \left\{
\begin{array}{]]}
\boldsymbol{q}_i \boldsymbol{k}^T_j & \text{if token }i\text{ attends to token }j, \\
-\infty & \text{if token }i\text{ does not attend to token }j,
\end{array}
\right.
$$
つまり、シーケンス中の\(i\)の位置のトークンベクトルが、\(j\)の位置のトークンベクトルに注目を向けないところは、\(-\infty \)にしてしまうのです。あれ、これってMask操作と同じではないかと思った方、鋭いです!
TransformerのDecoderでは先読みしないように\(j>i\)のトークンベクトルは使用しないようにマスクされていたわけです。その時のAttention Matrixは以下のようになっています。

一旦、Decoderの話は置いておくとしつつも、このように注意を向けない部分を用意して、スパースにするということです。
このSparse Attentionを具体的な式に落とし込むと下のようになります[3]。
接続パターン\(S=\{S_1, \cdots, S_n\}\)において、\(S_i\)は\(i\)番目の出力ベクトルが入力ベクトルのセットを表します。
$$
\text{Attend}(X, S) = \left(a(\boldsymbol{x}_i, S_i)\right)_{i\in\{1,\cdots,n\}}
$$
$$
a(\boldsymbol{x}_i, S_i) = \text{softmax}\left(\frac{(W_q \boldsymbol{x}_i) K^T_{S_i}}{\sqrt{d}}\right)V_{S_i}
$$
$$
K_{S_i} = \left(W_k\boldsymbol{x}_j\right)_{j\in S_i}, V_{S_i} = \left(W_v\boldsymbol{x}_j\right)_{j\in S_i}
$$
\(j\in S_i\)で使用する情報を制限しているので、\(K_{S_i}\)のサイズが小さくなっていることが理解できると思います。
ここで、\(S_i = \{j:j\le i\}\)とすれば、DecoderのAttentionになります。
Sparse Attentionの種類
Sparse Attentionの種類について説明します。Sparse Attentionの接続パターン\(S\)を学習により獲得するか、決め打ちにするかで分類することができます。前者をDynamic Sparse Attention[5]、後者をStatic Sparse Attentionといいます。Static Sparse Attentionには、全体に注意を向けられる成分を持つGlobal Attentionと、局所的な注意に特化したLocal Attention、ランダムに注意を向けるRandom Attentionなどがあります。それらのAttention Matrixは下図のようになります。そして、これらは単体で使われるというよりは、Global AttentionとLocal Attentionを組み合わせる使い方が一般的です。
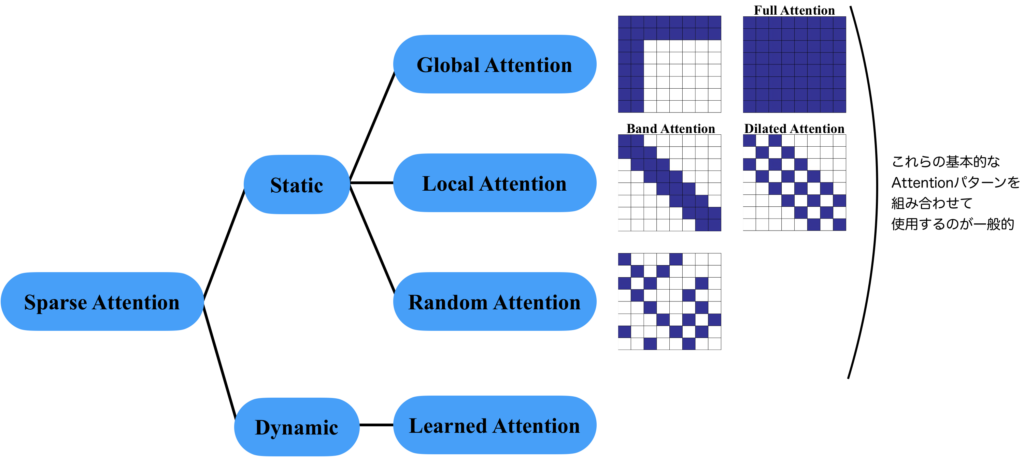
表現能力はSparseで十分なのか
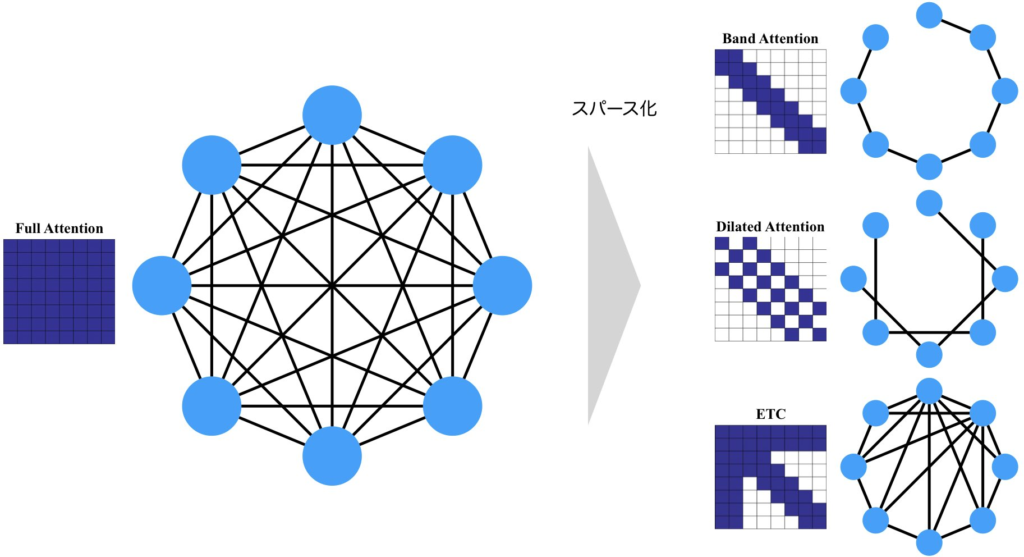
任意のトークンは、他の全てのトークンに注意を向けられるべきでしょう。しかし、学習された注意表現はスパースであることが多いので、構造的にスパースにしてしまっても問題はないのではないかというのがアイディアのベースにあります。Sparse Attentionの接続関係をグラフとして考えてみると分かりやすいです。全てが接続されている完全2部グラフは、Full Attentionを表します。1層のAttentionでは、直接接続されているノード同士の情報のみを考慮することができます。しかし、多層になると、何回か辺を辿ることで到達できるノードの情報も考慮することが可能になります。つまり、下図のBand Attentionであれば、1層で考慮できるのは、自分自身と隣り合った2つのノードのみですが、複数の層を重ねることで、隣接していない遠くのノードの情報も考慮することが可能になります。Dilated Attentionは興味深いことに、完全に2つに分かれていて、重ならないので、何層スタックしても、全てを考慮することはできません。つまり、何が言えるかというと、最下層のETCに示すように、複数のAttentionパターンを組み合わせて使うことが重要になるのです。
まとめ
この記事では、Sparse Attentionについて解説してきました。Sparse Attentionは、Attention Matrixをスパースにすることで、計算量を大幅に削減し、効率的な学習を可能にする技術です。具体的には、Global Attention、Local Attention、Random Attention、それらを組み合わせたAttentionなど、さまざまなSparse Attentionの形式があります。これらの技術は、Transformerのパフォーマンスを向上させるための重要な手段となります。
参考文献
[1] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin, "Attention is all you need," in Proc. NeurIPS, 2017.
[2] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby, "An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale," arXiv, 2020.
[3] Rewon Child, Scott Gray, Alec Radford, and Ilya Sutskever, "Generating Long Sequences with Sparse Transformers," CoRR, 2020.
[4] Tianyang Lin, Yuxin Wang, Xiangyang Liu, and Xipeng Qiu, "A Survey of Transformers," arXiv, 2021.
[5] Liu Liu, Zheng Qu, Zhaodong Chen, Yufei Ding, and Yuan Xie, "Transformer Acceleration with Dynamic Sparse Attention," arXiv, 2021.


