Deep Learning アドベントカレンダー2日目の記事では、現在の深層学習の基礎となる人工ニューラルネットワーク(Artificial Neural Network:ANN)のホップフィールドネットワーク(Hopfield Network)について学んでいきたいと思います。
アブストラクト
まず、ホップフィールドネットワークの要点と、それを学ぶことで得られる知見を先に示したいと思います。
ホップフィールドネットワークの要点
以下にポイントとなる性質・語句を示します。
- 自己結合をもたない相互結合型ニューラルネットワーク
- 相互結合の重みは等しい
- 決定論的ニューロン
- ヘブ則
- エネルギー関数
ホップフィールドネットワークは自己結合をもたない相互結合ニューラルネットワークで、相互結合(\(w_{ij}=w_{ji}\))の重みは等しいです。そして、ニューロンは決定論的ニューロンが使用され、具体的にはマカロック・ピッツ型の人工ニューロンが使用されます。学習は、近くの細胞が同時に発火すると関連性が高いとして結合を強くするヘブ則(Hebb's rule)が使用されます。これだけの知識でホップフィールドネットワークの学習や想起は実現できますが、連想記憶を実現する際にネットワークの状態が分かると便利です。そこで、想起のステップごとに値が減少するエネルギー関数を導入します。
ホップフィールドネットワークを学ぶことで得られる知見
以下に、ホップフィールドネットワークを学ぶことで得られる知見を示します。
- 生物学的な妥当性のあるヘブ則による学習が可能であることが体験できる
- 局所解が生まれる原理・どう対処したらいいかという基礎的な考えかたを学べる
まず、生物学的妥当性のあるヘブ則による学習が可能であることが体験できるというのは、いまのニューラルネットワークの学習で重要な誤差逆伝播は生物学的な妥当性がないため、より生物学的な学習メカニズムに近い形で生物の知が生まれる仕組みを体験できます。二つ目の、局所解が生まれる原理・どう対処したらいいかという基礎的な考えかたを学べるというのは、以下の実験で順番に文字を学習させていきますが、あるときから、急に収束先が疑似パターン、すなわち局所解に陥るようになります。大規模な深層学習を行う際、パラメータ数や学習データ数が多いため、たとえ局所解に陥っていても、あまり目立たないことが多い一方で、ホップフィールドネットワークは局所解に収束するのが目に見えて体験できます。この対処法を考えることで、次回のボルツマンマシンへ話を繋げていくことができます。
ホップフィールドネットワークとは
ホップフィールドネットワークとはアメリカの物理学、生物学者のジョン・ホップフィールドが提案した相互結合型ニューラルネットワークで、人工ニューロンが集団状態として情報を記憶するモデルで連想記憶を実現することができます。生物の脳の海場は短期記憶で広く知られていますが、海場は連想記憶を得意としており、このホップフィールドネットワークは海馬を抽象化したモデルと捉えることが可能です。
以下の図はホップフィールドネットワークのモデルを示したものです。無向グラフで実現されている点に注目してください。
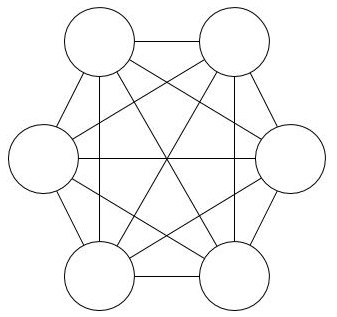
ホップフィールドネットワークの定式化
ホップフィールドネットワークは普段私たちが一般的に使用するフィードフォワード型ニューラルネットワーク(Feedforward Neural Network:FNN)の学習方法とは異なる部分が多々あります。ここでは、最初にニューロンを定式化、ヘブ則を定式化し、エネルギー関数について紹介します。
マカロック・ピッツの形式ニューロンの定式化
マカロック・ピッツの形式ニューロンは神経生理学者のウォーレン・マカロック(Warren Sturgis McCulloch)と論理学者であり数学者でもあるウォルター・ピッツ(Walter J. Pitts)によりモデル化された人工ニューロンで、ニューロンの複雑なふるまいを数学的に簡単な式で表現したものです。
まずは、以下のニューロンの図において、前半部分(黒線で囲った部分)を数式化してみます。前半で行われることは、シナプス前ニューロンからの入力の空間的加算と時間的加算です。ここでは、空間的加算のみ数式化します。
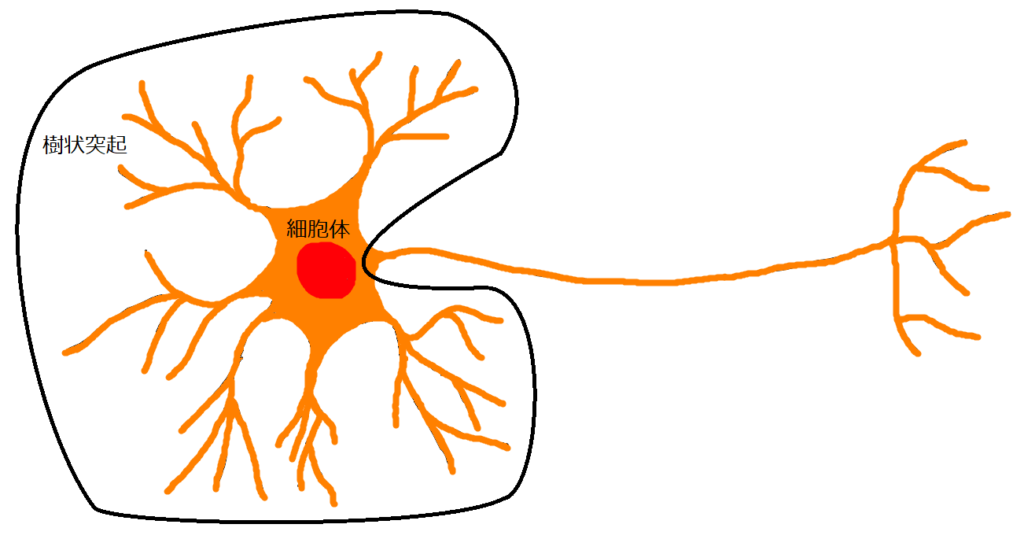
シナプス前ニューロンからのデータを\(x_i\)、シナプスの結合重みを\(w_i\)とし、またバイアスを\(\theta\)とします。このとき、ニューロン前半部分では
$$
u = \sum_{i=1}^nw_ix_i + \theta
$$
のように計算が行われることが分かります。
次に、後半部分(黒線で囲っていない部分)を定式化します。ここでは、前半で計算された値が正過負荷に応じて階級関数で離散化する操作になるので、
$$
f(u) = \left\{
\begin{array}{ll}
1 & if\ \ u >= 0\\
0 & if\ \ u < 0
\end{array}
\right.
$$
と写像する単位ステップ関数を考えます。これにより、マカロック・ピッツ型の人工ニューロンは、
$$
f\left(\sum_{i=1}^nw_ix_i + \theta\right)
$$
となります。
ホップフィールドネットワーク用に少し拡張
ここでは、先ほど定義した人工ニューロンを相互結合型に合わせた表記、時間的概念を導入した表示に変更していきます。
\(n\)個のニューロンからなる相互結合ニューラルネットワークを考えます。このとき、\(i\)番目のニューロンに注目し、\(j\)番目のニューロンとの結合重みを\(w_{ij}\)、バイアスを\(\theta_i\)とします。時刻\(t\)の\(j\)番目ニューロンからの入力\(x_j(t)\)より、重み付き和として、以下のように\(u_i(t)\)を書き換えます。
$$
u_i(t) = \sum_{j=1}^nw_{ij}x_j(t) + \theta_i
$$
このとき、\(u_i(t)\)の値をステップ関数に適用します。
$$
x_i(t+1) = \left\{
\begin{array}{ll}
1 & if\ \ u_i(t) > 0\\
x_i(t) & if\ \ u_i(t)=0\\
0 & if\ \ u_i(t) < 0
\end{array}
\right.
$$
これで、ホップフィールドネットワーク用にニューロンの定義ができました。
※注意点として自己結合はありませんので、\(w_{ii}=0\)となります。
学習の定式化
ヘブ則
ヘブ則とは心理学者のヘブが唱えた自己組織化学習において重要なシナプス可塑性のルールのことです。バックにある考え方は信号伝達の効率化で、ニューロンとニューロンの間を信号が通り抜けたら、その部位のシナプスを増強し信号が通りやすくしようという単純なルールです。

上の図は、左のニューロンが反応したとき、右のニューロンも似たような反応を示したので、結合を強くしたことを表しています。
これを式で表現するのは簡単で、
$$
w_{ij} \leftarrow w_{ij} + \Delta w_{ij}\ \ (= w_{ij} + \eta\ x_ix_j)
$$
となります。ニューロンの出力の近さは内積で表されるので、その値を更新前の重みに足せばいいのです。\(\eta\)は学習係数ですが、1にして問題ありません。
記憶パターンを教える
記憶はホップフィールドネットワークの全ニューロンの状態で表されます。そのため、教える記憶の形状は、ホップフィールドネットワークのニューロン数を\(n\)とすると、ベクトル\((x_1, x_2, x_3, \cdots, x_n)\)で表されます。ただし、この表記だと、記憶が複数ある場合の定式化がしにくいので、一般に、\(Q\)個の記憶を\((x^s_1, x_2^s, x^s_3, \cdots, x^s_n)\)ただし\(s=1,2,\cdots, Q\)と表記することにします。右肩にある文字\(s\)は記憶の状態stateのsです。
それでは、\(w_{ij} \leftarrow w_{ij} + \Delta w_{ij}\ \ (= w_{ij} + \eta\ x_ix_j)\)に従って、学習をさせようと思いますが、この式は、1つづつパターンが与えられた時の学習方法であり、さきに記憶すべきデータがすべてそろっている場合は、以下のように簡単に数式化できます。
重みはヘブ則より
$$w_{ij} = \frac{1}{Q}\sum_{s=1}^Qx^s_ix^s_j$$
で計算でき、\(s\)番目の状態を行ベクトル\(\boldsymbol{x}^s\)で表すと、さらに
$$W = \frac{1}{Q}\sum_{s=1}^Q(\boldsymbol{x}^s)^T\boldsymbol{x}^s$$
と計算できます。
想起の定式化
想起とは以前のことを思いだすことをいいます。既に特定の記憶を学習したホップフィールドネットワークは任意の入力からその記憶を連想することができます。では、どのように連想していくのか説明していきたいと思います。
まず、任意の入力ベクトル\((x_1, x_2, x_3, \cdots, x_n)\)が与えられたとします。これは、ホップフィールドネットワークの初期状態を表す状態ベクトル\(s(0)=(x_1(0), x_2(0), x_3(0), \cdots, x_n(0))\)になります。ここで、ランダムにニューロンを1つ選びます。ここでは、\(i\)番目のニューロンを選んだとします。このとき、先ほど示した式で、まず\(u_i(0)\)を求め、次の出力\(x_i(1)\)を求めます。この際、新しく求まった状態は、\(s(1) = (\cdots, x_i(1), \cdots)\)となります。後で説明しますが、状態\(s(t)\)から状態\(s(t+1)\)に遷移する前後でエネルギー関数の値は必ず減少し、ネットワークは安定状態に近づきます。これを簡潔に表すと、
- \(n\)個のニューロンから1つランダムに選ぶ
- 上で選んだニューロンの値を更新する。
を繰り返すことになります。これを繰り返せば繰り返すほど連想記憶は鮮明になります。しかし、どこまで繰り返すかの指標は必要で、それが次に説明するエネルギー関数になります。
エネルギー関数
上で説明したように、ネットワークが安定しているかどうかの指標が必要です。物理法則に目を向ければ基本的にエネルギーが高い状態から低い状態に遷移しようとします。ホップフィールドネットワークも同じで初期状態からより初期に覚えた記憶に収束しようと遷移します。このとき、以下のような式を定義すると、遷移によってエネルギーが減少するような状況を表現できました。
$$
E(t) = -\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^nw_{ij}x_i(t)x_j(t) - \sum_{i=1}^n\theta_ix_i(t)
$$
これをエネルギー関数といいます。これは、物理法則でいう本当のエネルギーを表しているのではなく、関数の値の変化の性質がエネルギーが収束し安定状態に遷移することを表しているように見えるため、エネルギー関数と名付けられただけのようです。
ホップフィールドネットワークで連想記憶を試す
ここでは、単純なホップフィールドネットワークを実装してみようと思います。
事前知識となる状態(記憶パターン)を埋め込む
まずは、記憶をネットワークに埋め込みしようと思います。これは、新しい未知の入力(ネットワークの状態)がきたときに連想可能なディスティネーションとなる状態を定義していることにつながります。
まずは、必要なライブラリをインポートします。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltつぎに、予め記憶させておくデータを作成します。
# 文字画像を格納するための配列を用意
x_n = np.full((7, 7), -1)
x_e = np.full((7, 7), -1)
x_u = np.full((7, 7), -1)
x_r = np.full((7, 7), -1)
x_a = np.full((7, 7), -1)
x_l = np.full((7, 7), -1)
# すべての配列をリストとして管理
X = np.array([x_n, x_e, x_u, x_r, x_a, x_l])
# 黒く塗りつぶすピクセルの位置を指定
list_N = [2, 6, 9, 10, 13, 16, 17, 20, 23, 25,
27, 30, 33, 34, 37, 40, 41, 44, 48]
list_E = [2, 3, 4, 5, 6, 9, 16, 23, 24, 25, 26,
27, 30, 37, 44, 45, 46, 47, 48]
list_U = [2, 6, 9, 13, 16, 20, 23, 27,
30, 34, 37, 41, 45, 46, 47]
list_R = [2, 3, 4, 5, 9, 13, 16, 20, 23, 24,
25, 26, 30, 34, 37, 41, 44, 48]
list_A = [3, 4, 5, 10, 12, 16, 20, 23, 24, 25,
26, 27, 30, 34, 36, 37, 41, 42, 43, 49]
list_L = [2, 9, 16, 23, 30, 37, 44, 45, 46, 47, 48]
# 塗りつぶす位置を保持するリストをまとめてリストとして保持
List = [list_N, list_E, list_U, list_R, list_A, list_L]
# 配列と塗りつぶし位置のリストを受け取り指定の位置を塗りつぶす関数
def make_img(x, lis):
for i in range(7):
for j in range(7):
num = 7*i + j+1
if num in lis:
x[i, j] = 1
# 塗りつぶす
for x, lis in zip(X, List):
make_img(x, lis)ここで、定義した状態である画像を可視化してみます。
# 可視化
plt.figure(figsize=(20, 5))
for i in range(6):
plt.subplot(1, 6, i+1)
plt.imshow(X[i], cmap=plt.cm.gray_r)すると、以下の図が表示されます。これが事前に記憶させておく、つまり連想記憶としてよみがえる既知の状態となります。画像は7x7です。

ネットワークの重み計算(学習)
7×7の画像なので、ホップフィールドネットワークのニューロン数は49個です。
先ほど示したように
$$W = \frac{1}{Q}\sum_{s=1}^Q(\boldsymbol{x}^s)^T\boldsymbol{x}^s$$
とまとめて計算することができます。
# ホップフィールドネットワークの重みを定義
neuron_num = 49
Q = 6 # 事前に記憶するパターン数(N,E,U,R,A,Lの6つ)
weight = np.zeros((neuron_num, neuron_num))
# # 1つずつ重みを計算する場合
# for i in range(neuron_num):
# for j in range(neuron_num):
# if j != i: # 自己結合はない
# w_ = 0
# for x in X:
# x_i = x.reshape((-1, neuron_num))[0][i]
# x_j = x.reshape((-1, neuron_num))[0][j]
# w_ = w_ + x_i * x_j
# weight[i, j] = w_ / Q
for x in X:
weight += np.dot(x.reshape((-1, neuron_num)).T, x.reshape((-1, neuron_num)))
weight /= Q
# 対角成分を0にする
musk = (np.eye(49) == 0)
weight *= musk重みを可視化してみます。
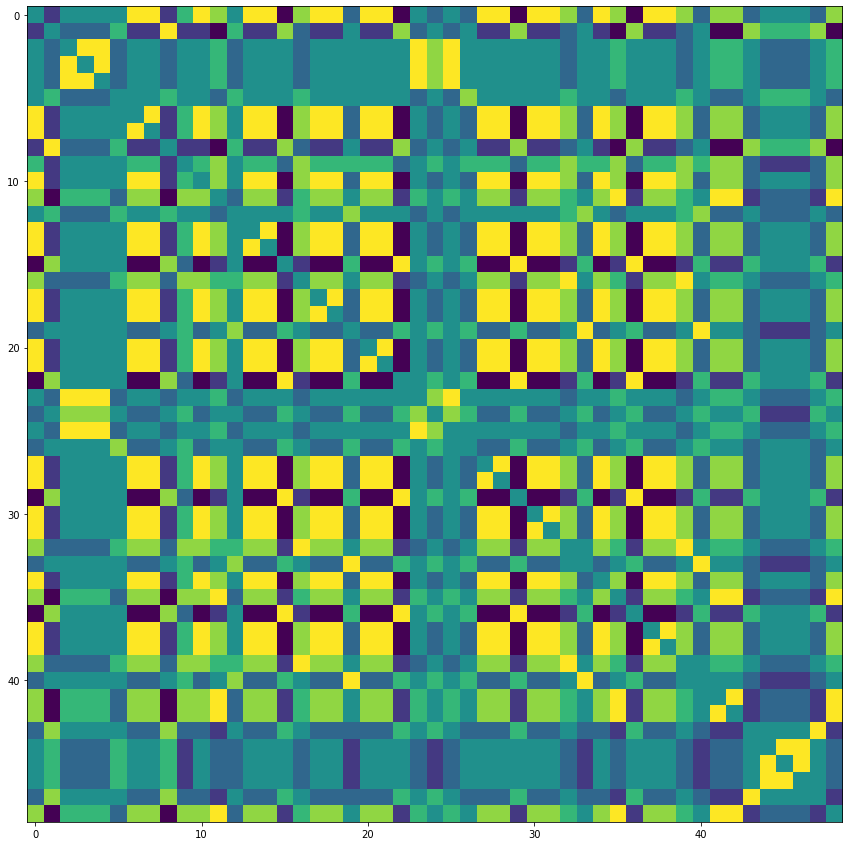
想起させてみる
ランダムな初期状態の配列を生成します。
# 入力データをランダム値で生成
random_input = np.random.randint(-1, 2, (1, 49))
plt.imshow(random_input.reshape((7, 7)), cmap=plt.cm.gray_r) # 初期状態の可視化この初期状態から、ホップフィールドネットワーク全体の状態が安定するまで更新します。1回の更新では変化するのはランダムに選ばれた1つのニューロンなので、今回のように49個のニューロンからなるホップフィールドネットワークはすべてのニューロンを更新するのに最低でも49ステップは必要になります。ここの例では単純化のため、定常状態に達したかの判定行わず、ひたすら1000回更新させます。
num = 1000
for i in range(num):
# ランダムにニューロンを選ぶ
neu_rand = np.random.randint(0, 49, 1)
# ランダムに選んだニューロンの値を導く
u = np.dot(weight[neu_rand][0], random_input[0])
if u > 0:
random_input[0][neu_rand] = 1
elif u < 0:
random_input[0][neu_rand] = 0
plt.imshow(random_input.reshape((7, 7)), cmap=plt.cm.gray_r) # 定常状態の可視化まずは、でたらめな入力で試してみます。上が入力した初期状態、下がその入力に対する結果を可視化したものになっています。

本来は元画像に多少のノイズを加えたものを入力した方が、連想記憶を実感できていいのかもしれませんが、完全にノイズの画像を入力しても、それなりに、尤もらしい記憶が復元されていることが見て取れると思います。
では、元の文字を入れて確かめてみましょう。結果は以下のようになりました。
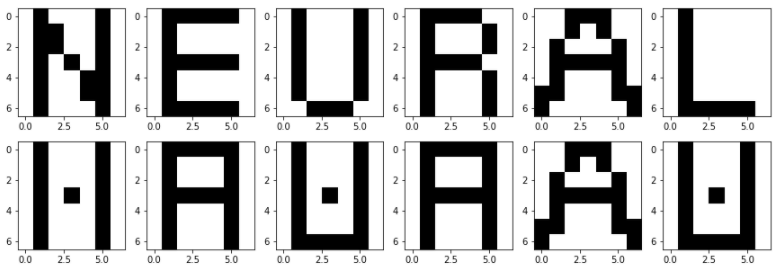
ありゃりゃ?!?!
もう1回やってみます。
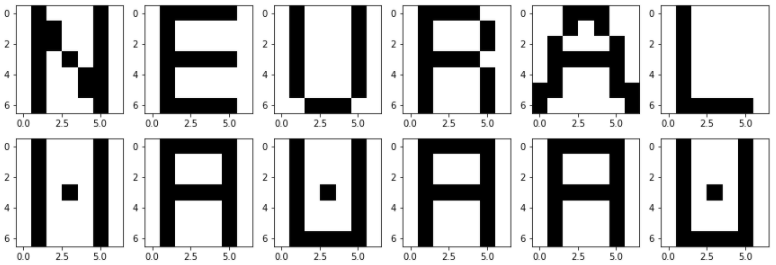
うーん。そもそも、記憶パターンを入力すればそこで安定しそうな気はしますが、そうではないようです。個人的に原因は以降で説明するクロストークや局所解による影響だけではなく、ネットワークの状態更新を非同期でおこなうか同期で行うかにもよるかなと思っています。結局、重みは各々の記憶パターンのヘブ則の平均になっているので、必ずしも安定状態を保てる重みになっているとは限りませんし、ランダムに1つのニューロンを選んで更新する非同期な更新にはランダム性が含まれるため、どのニューロンを選んだかによって、収束するパターンが異なる可能性は十分にあり得ると考えられます。
先ほど少し話に出したクロストークと局所解ですが、記憶させた画像の性質が似ていることに起因して、予期した記憶とちがう記憶が連想されてしまうのが前者で、学習していないはずのパターン(疑似パターン)を連想してしまうのが後者によるものです。
クロストーク
準備
上で説明たように、クロストークは似た性質の画像が学習されるために起因します。ではどうしたらいいでしょうか。まず、以下の例を見て見ましょう。画像をベクトルとして内積を計算して類似さを数値化してみます。ここで、類似度の大きい画像同士が重ならないように選別します。以下が画像同士の内積をとった結果です。
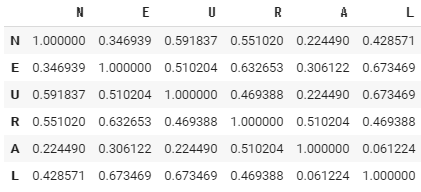
内積が小さいもの同士の組み合わせとして、N、E、Aを選び、それだけを学習させてみたいと思います。まずは重みを初期化します。
# ホップフィールドネットワークの重みを定義
neuron_num = 49
Q = 3 # N,E,Aの3つ
weight = np.zeros((neuron_num, neuron_num))
for x in X[[0, 1, 4]]:
weight += np.dot(x.reshape((-1, neuron_num)).T, x.reshape((-1, neuron_num)))
weight /= Q
# 対角成分を0にする
musk = (np.eye(49) == 0)
weight *= muskでは、学習させた文字を入れてみて、正しい状態に収束するか確認したいと思います。

この結果から、学習させた画像についてはひとまず正しく連想できることが分かりました。それでは、手書き文字認識みたいに、いくつか雑音を入れた文字を入力してみたいと思います。

正しく連想できていることが分かります。
記憶の直交化による対処
準備で内積が小さい画像同士、つまり直交関係に近い画像同士を学習させるのであればクロストークが発生しにくいことが分かりました。では、似ている画像を覚えさせるのは諦めなければいけないのでしょうか?そんなことはありません。直交関係に近いほどクロストークが生じにくいことをより大きくとらえれば、記憶させる前に覚えさせる画像を直交化してしまえばいいことになります。具体的には、一般化逆行列を使用して記憶パターンを直交化して、重みを定義します。重み学習の方法を以下に示します。
再度確認ですが、ここでは各々のデータは列ベクトルではなく行ベクトルで考えます。\(s\)番目の学習パターンを\(\boldsymbol{x}^s\)としたとき、
$$
X^T = ((\boldsymbol{x}^1)^T, (\boldsymbol{x}^2)^T, \cdots, (\boldsymbol{x}^Q)^T)
$$
を定めます。ここで、学習パターン数\(Q\)とホップフィールドネットワークのニューロン数を\(n\)とすると、\(X\)は\(Q×n\)行列になります。このとき、以下の2つに場合分けして一般化逆行列\(X^+\)を定義して、重み行列\(W\)を定義します。
- \(Q<n\)
$$X^+ = X^T(XX^T)^{-1}$$
$$W = X^+X$$ - \(Q>n\)
$$X^+ = (X^TX)^{-1}X^T$$
$$W = XX^+$$
本記事の例では1のやり方で実施することになります。\(W\)を定義する部分のプログラムは
weight = (X.T@np.linalg.inv(X@X.T))@Xとするだけです。このとき、それぞれの入力に対する連想結果は
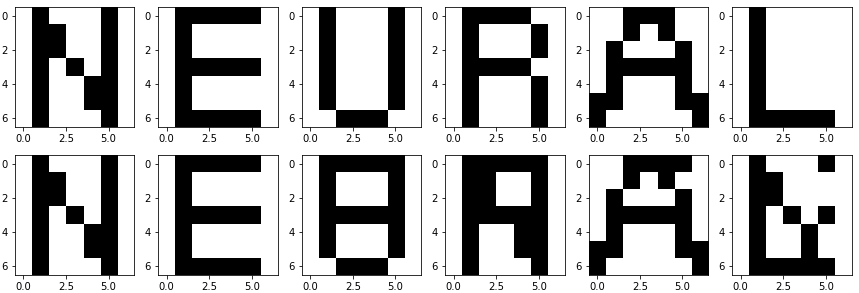
となりました。どうでしょう。直交化したときの方が、直交化していないときより性能がいいように感じます。
最後にホップフィールドネットワークが正しく想起できる可能な容量ですが、一般的にニューロン数の15%程度のパターンまでとされています。これは、今説明してきたクロストークがかなりかかわっていて、それより多いパターンを学習させると、別のパターンを連想してしまうようになります。今回は、49個のニューロンがあるので、最大で7個までなら頑張れば大丈夫でしょうというところです。かなり効率が悪いですね。
局所解への収束
ここでは、見たことのないパターンに収束してしまう時について考えていきます。先ほどまでの結果を見てきて、気が付いておられる方もいると思いますが、なぜか似ているようで似ていないような微妙なパターンに収束してしまっているときが多々あります。これは、局所解に収束してしまっている状態です。局所解はエネルギー関数をグラフ化した際に学習パターン部分が最適解になるはずが、そのほかに局所解が発生して、そこに収束してしまったことに起因します。
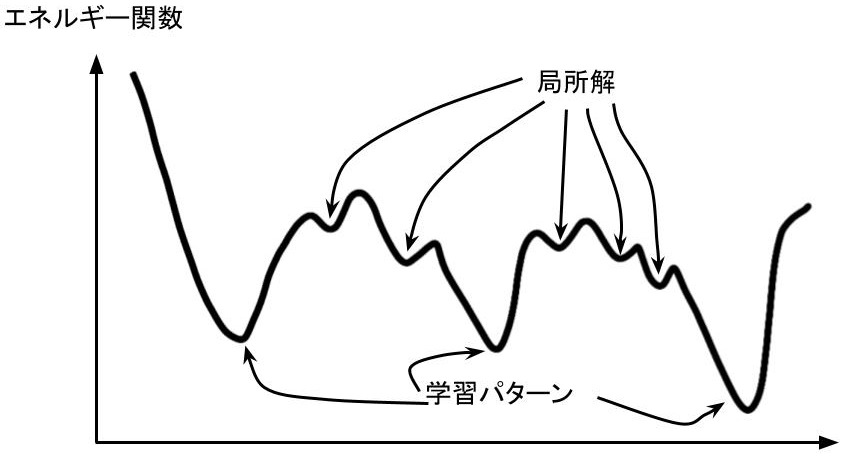
この対処法は次の記事で扱うボルツマンマシンで解説したいと思います。
まとめ
前半に記した要点を再度ここで示します。今回扱ったホップフィールドネットワークは自己結合をもたない相互結合ニューラルネットワークで、連想記憶のモデルです。相互結合(\(w_{ij}=w_{ji}\))の重みは等しく、決定論的なニューロンが使用され、重みの学習は生物学的な妥当性のあるヘブ則(Hebb's rule)が使用され、ネットワークが定常状態に達したかの判定はエネルギー関数によって判定可能です。
想起に際してはクロストーク、局所解への収束が結果に大きく関与していることは知られています。また、今回は同期・非同期について実験ができていないのですが、これも想起の結果に大きな影響を与えていると考えられます。本記事ではクロストークについて扱い、次回は、ボルツマンマシンの話で局所解から抜け出す方法を説明します。
