前回の記事では誤差逆伝播を導きました。より一般化した式で説明するよう心掛けたので、具体性には欠けるものとなっていました。特に、活性化関数の導関数に関してはソフトマックス関数の話を除き、基本的には指定しませんでした。今回の記事ではさまざまな活性化関数\(f\)とその導関数\(f'\)について紹介するので、誤差逆伝播と絡めながら更に理解を深められればと思います。
活性化関数とは
まず最初に、活性化関数について概要を説明します。活性化関数とは、人工ニューロンの構造の一部を成す重要な要素です。ニューロンには入力に重み掛けして和をとる操作と、その値を何らかの関数(=活性化関数)で写像する操作の2ステップの処理からなっています。
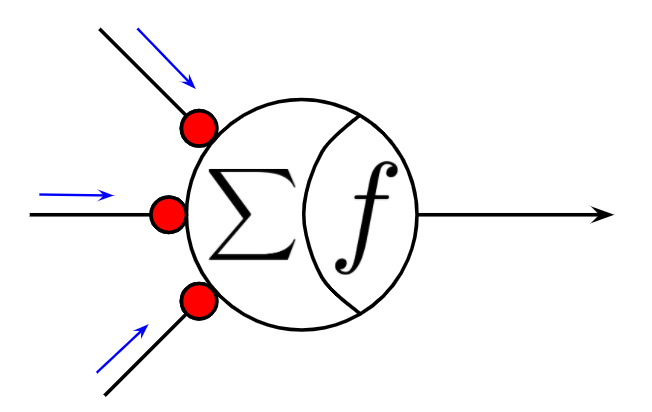
ちなみに、この計算上の2ステップは生物学的なニューロンを高度に抽象化したもで、実際の生物学的なニューロンでも、活性化関数らしき働きを内部に持っています。この、2つの処理は、どちらもニューロンの性質に影響を与える重要な要素であるわけですが、柔軟性が異なります。1つ目の重み掛けして和をとる操作は、ニューロンの性質を決定する大きな要因であるとはいえ、学習により変化することができるため、分かりやすく言えば後天的な特徴であると考えることができます。一方で、2つ目の活性化関数による写像というのは、ニューラルネットワークを定義する時点で人間が指定するものであるため、基本的には、先天的に決定される特徴と考えることができます。ですので、本記事で扱うのは、学習のアルゴリズムのようなシステマティックな内容ではなく、ニューラルネットワークにどのような可能性を与えてあげられるかという人間側が知っておかなければいけない内容になると考えています。
つぎに、活性化関数の役割について説明します。活性化という言葉自体は化学だったり神経科学だったりいろいろな場面で使用されますが、端的に言えば活性状態へ化する変化を表現しているわけで、活性化関数は、ニューロンが活性状態へ化する(脱分極する)変化を関数として表現しているものと解釈できるでしょう。このとき、その変化は非線形的なものが望ましく、非線形性がネットワーク全体としての表現能力を大幅に上げることに関与しています。
活性化関数の歴史を顧みるとき、個人的にはマカロック・ピッツの形式ニューロンモデルやそれ以前のモデル、玄人からは素人が何を言っている!!といわれそうですが、極端な話、Hodgkin-Huxley方程式まで遡って学びたいなと思っていたのですが、そこまで学びが進まなかったので、今回は諦めました。使用される活性化関数の過去から現在への変化を顧みると、もとは、生物学的なニューロン活動の変化を抽象的に表すものだったのが、最近では誤差逆伝播の普及とともに形が変化し、誤差逆伝播でしっかりと学習ができるもの、つまり、誤差逆伝播と相性の良いものへ変化してきています。後で説明しますが、勾配消失問題への試行錯誤の結果として、現在ではReLUファミリーが大きな権力を握っています。
余談ばかりになってしまったのですが、ここまでをまとめると、活性化関数というのは、人間がニューラルネットワークを定義する際に、人間がネットワークに先天的な能力として定義してやる関数で、また非線形性というのが重要な鍵になっていますって話です。
活性化関数と勾配消失問題
誤差逆伝播の式を思い出してみましょう。ここに行列計算の場合の誤差逆伝播の式を再掲します。
$$\begin{eqnarray}
\boldsymbol{W}^{(l)}&=&\boldsymbol{W}^{(l)}-\eta\nabla J(\boldsymbol{W}^{(l)})\\
&&(-\eta\nabla J(\boldsymbol{W}^{(l)})=\Delta\boldsymbol{W}^{(l)})\\
\Delta\boldsymbol{W}^{(l)}&=&-\eta \frac{1}{N}\boldsymbol{\mathcal E}^{(l)}(\boldsymbol{Z}_{ex}^{(l-1)})^T\\
\mbox{ただし }\boldsymbol{\mathcal E}^{(l)}&=&\left\{\begin{array}{ll}
\boldsymbol{\mathcal E}^{(l)} = (\boldsymbol{Z}_{ex}^{(l)}[bias:] - \boldsymbol{T})\odot f'_l(\boldsymbol{U}^{(l)})&\mbox{\(l\)が出力層(\(l=L\))}\\
\boldsymbol{\mathcal E}^{(l)} = (\boldsymbol{W}^{(l+1)}[:, bias:])^T\boldsymbol{\mathcal E}^{(l+1)}\odot f'_l(\boldsymbol{U}^{(l)})&\mbox{\(l\)が中間層(\(l<L\))}
\end{array}\right.
\end{eqnarray}$$
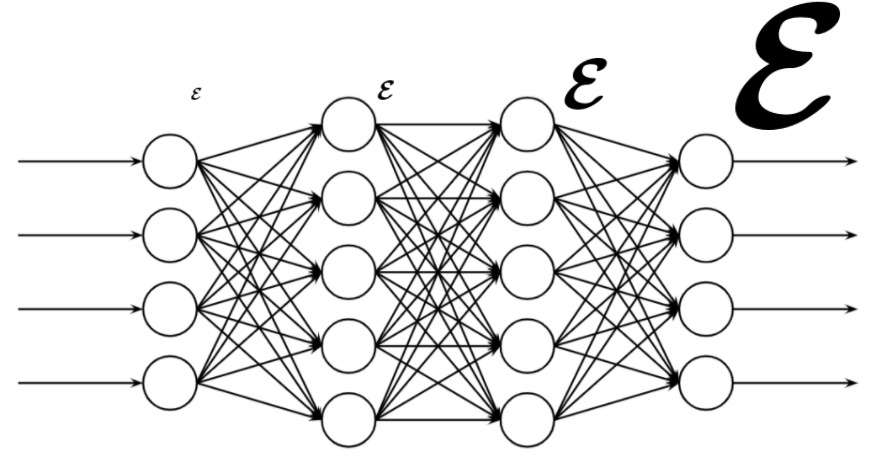
でしたね。ここで、注目すべきなのは、誤差が逆伝播される毎に、活性化関数の導関数が掛け合わされている点です。そのため、極論ですが、導関数の値が0.1だったら、伝播できる誤差は0.1倍程度に減少すると考えられます。もし、何十層、何百層という深層ネットワークだったら、何度も活性化関数の微分値が掛け合わされることで誤差が途中で消失してしまうことが容易に想像できます。誤差が消失してしまった場合、誤差の伝わらない層に存在意義はありませんので、単なるメモリや計算コストの無駄となります。このように、活性化関数の導関数が掛け合わされることで勾配が生じてしまう問題を勾配消失問題といいます。嘗てのニューラルネットワークで主流だったロジスティック関数の導関数は最大値が0.25なので、勾配消失がしばしば起こりました。そこで、ロジスティック関数の導関数よりは最大値が大きい双曲線正接関数(tanh)が使われるようになりました。双曲線正接関数の導関数は最大値が1ではありますが、0以外の領域では導関数の値が1を下回るため、やはり勾配消失問題は防げませんでした。そこで、位置によらず導関数の値が一定の恒等関数(線形関数の一種)に非線形性を持たせた正規化線形関数ReLUが注目を浴びることになりました。基本的に、ReLUファミリーは正の領域で導関数の値が常に1になります。
これだけは!(大まかな分類)
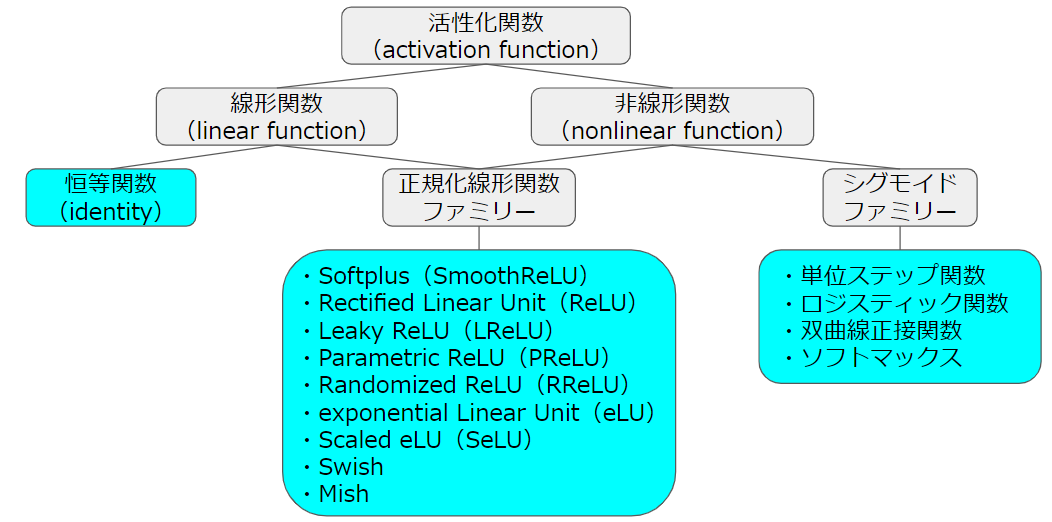
以降から、ずらずらと様々な活性化関数を紹介していきますが、その前に、活性化関数を大まかに分類したいと思います。まず、活性化関数は線形関数と非線形関数に大別されます。線形関数には恒等関数、非線形関数には単位ステップ関数やロジスティック関数(基本的にはこれをシグモイド関数と呼んでいる)を代表とするシグモイドファミリーがあります。しかし、恒等関数は多層ニューラルネットワークの中間層に採用するのは好ましくないです。理由は、多層にすることの目的は重み行列による線形写像に活性化関数による非線形写像を適用する工程を繰り返すところにあるからです。そのため恒等関数を使用してしまうと全ての写像が一貫して線形になってしまい、ネットワークの表現能力は単一の行列で表される線形写像で実現できる範囲に制限されてしまいます。また、シグモイドファミリーも恒等関数と同様に中間層へ使用するのは望ましくありません。理由は勾配消失問題により層を深くすることが困難だからです。ですので、昔の浅いニューラルネットワークであれば、シグモイド関数を中間層に使用しても大して問題にはなりませんでしたが、近年のディプラーニングブームを飾るような深層ニューラルネットワークでは使用することはできません。そこで、線形関数の良さと非線形関数の良さを併せ持つ関数である正規化線形関数(ReLU)ファミリーが中間層で使用されるようになりました。正規化線形関数ファミリーの導関数は正の領域であれば(ほぼ)一定で値は大抵1なので、活性化関数の微分を繰り返し乗算することに起因する勾配消失問題を避けやすくなりました。正規化線形関数ファミリーには元祖のReLUや、その平滑化近似のSoftplus(SmoothReLU)、負値の扱い方の違いによるLReLU、PReLU、RReLU、eLU、SeLUなどがあります。そして、近年高い評価を得ているSwishやMishなどはシグモイドファミリーと正規化線形関数ファミリーを融合したような位置づけになると思います。
代表的な活性化関数とその導関数
以下に、代表的な活性化関数とその導関数を示します。また、本来であれば導関数を定義できない活性化関数が多くありますが、それらは近似的に導関数を導入させています。
青:活性化関数自体のグラフ
オレンジ:微分のグラフ
です。
単位ステップ関数(step)
| $$ u(x)=\left\{\begin{array}{ll} 1&(x\geq 0)\\ 0&(x<0) \end{array}\right. $$ |
| $$ \frac{d}{d x}u(x)=\delta (x) $$ 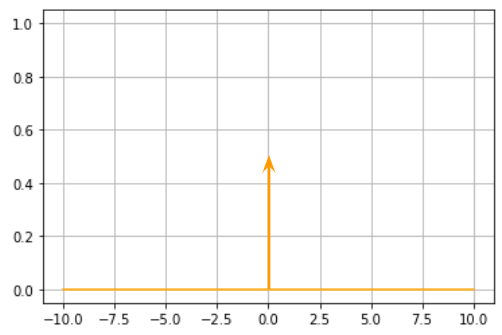 |
作成するパーセプトロンクラスには実装しないのでコードは省略します。
恒等関数(identity function)
| $$ \phi (x) = x $$ |
| $$ \frac{d}{d x}\phi (x)=1 $$ |
identity = lambda x: x # 恒等関数
identity_der = lambda x: np.ones(x.shape) # 恒等関数の微分シグモイド関数(sigmoid)
| $$ \sigma(x)=\frac{1}{1+e^{-x}} $$ |
| $$ \frac{d}{d x}\sigma(x)=\sigma(x)(1-\sigma(x)) $$ |
sigmoid = lambda x: 1/(1+np.exp(-x)) # シグモイド関数
sigmoid_der = lambda x: sigmoid(x)*(1-sigmoid(x)) # シグモイド関数の導関数ソフトマックス関数(softmax)
| $$ softmax(x_i)=\frac{e^{x_i}}{\sum_k e^{x_k}} $$ |
| $$ \frac{d}{d x_j}softmax(x_i)=\left\{\begin{array}{ll} softmax(x_i)(1-softmax(x_j))&i=j\\ -softmax(x_i)softmax(x_j)&i\neq j \end{array}\right.$$ 以下のグラフは、横軸\(x_j\)、縦軸\(\frac{d}{d x_j}softmax(x_i)\)で\(j\)は可変で\(i\)を固定したときの例 |
softmax = lambda x: np.exp(x)/np.exp(x).sum(axis=0) # ソフトマックス関数
softmax_der = lambda x: x*(1-x) # ソフトマックス関数の微分双曲線正接関数(tanh)
| $$ \tanh(x) $$ |
| $$ \frac{d}{d x}\tanh(x) = 1-(\tanh(x))^2 $$ |
tanh = lambda x: np.tanh(x) # 双曲線正接関数
tanh_der = lambda x: 1-np.tanh(x)**2 # 双曲線正接関数の微分Softplus(SmoothReLU)
Softplus関数は次に説明する正規化線形関数(ReLU)を滑らかに近似した関数で、SmoothReLUともいわれます。
| $$ softplus(x) = \log(1+e^x) $$ |
| $$ \frac{d}{d x}softplus(x) = sigmoid(x) $$ のように、Softplus関数の微分はシグモイド関数になります。 |
softplus = lambda x: np.log(1 + np.exp(x)) # softplus関数
softplus_der = lambda x: sigmoid(x) # softplusの導関数正規化線形関数:Rectified Linear Unit(ReLU)
| $$ relu(x) = max(0, x) $$ |
| $$ \frac{d}{d x}relu(x) = \left\{\begin{array}{ll} 1&(x\geq 0)\\ 0&(x<0) \end{array}\right. $$ のように、ReLUの微分は単位ステップ関数になります。 |
relu = lambda x: np.maximum(0, x) # ReLU
relu_der = lambda x: np.where(x>0, 1, 0) # ReLUの導関数Leaky ReLU(LReLU)
| $$ lrelu(x) = max(\alpha x, x) $$ ただし、\(\alpha=0.01\)のように小さい値とする。以下のグラフでは分かりやすくするために、\(\alpha=0.05\)としている。 |
| $$ \frac{d}{d x}lrelu(x) = \left\{\begin{array}{ll} 1&(x\geq 0)\\ \alpha &(x<0) \end{array}\right. $$ |
lrelu = lambda x, a=0.01: np.maximum(a*x, x) # LReLU, aはスカラー
lrelu_der = lambda x, a=0.01: np.where(x>0, 1, a) # LReLUの導関数, aはスカラーParametric ReLU(PReLU)
PReLUはLReLUにおける\(\alpha\)を学習対象のパラメータとするものです。ニューラルネットワークの各層に活性化関数を適用する際は、一括に指定するのが一般的ですが、PReLUでは層の各ニューロンごとにパラメータが最適化されるため、同一の層に属するニューロン同士であっても、活性化関数の形状は若干異なるものになります。プログラムでは、あたかも層単位で適用しているかのように扱うために、パラメータ\(\alpha\)をベクトル\(\boldsymbol{\alpha}\)とします。パラメータの学習には勾配降下法を使用するので、\(-\eta\frac{\partial E}{\partial \boldsymbol{\alpha}}\)を求める必要があります。
| 入力ベクトル\(\boldsymbol{x}\)、各ニューロンのPReLUのパラメータ\(\boldsymbol{\alpha}\)より、 $$ prelu(\boldsymbol{x}) = max(\boldsymbol{\alpha}\odot \boldsymbol{x}, \boldsymbol{x}) $$ ※グラフはLReLUと同じなので省略 |
| $$ \frac{d}{d \boldsymbol{x}}prelu(\boldsymbol{x}) = \left\{\begin{array}{ll} \boldsymbol{1}&(\boldsymbol{x}\geq \boldsymbol{0})\\ \boldsymbol{\alpha} &(\boldsymbol{x}<\boldsymbol{0}) \end{array}\right. $$ ベクトルの各成分同士を比較して、その成分に対応する適切な値を返します。 ※グラフはLReLUと同じなので省略 |
prelu = lambda x, a: np.maximum(a*x, x) # PReLU, aはベクトル
prelu_der = lambda x, a: np.where(x>0, 1, a) # PReLUの導関数, aはベクトルRandomized ReLU(RReLU)
これは紹介だけにします。ここまで、ReLUに負の入力をしたときの振る舞いとして、完全に0のものをReLU、定数のスカラー\(\alpha\)分だけ入力値を漏らしたものをLReLU、入力を漏らす量自体を学習で決めるのがPReLUを扱いました。勘のいいひとだと、漏らす量をランダムにしたらどうなの?と思うかもしれませんね。まさに、このようなReLUがあって、それをRReLUといいます。詳細は省略します。
exponential Linear Unit(eLU)
先ほどまで述べてきた様々な種類のReLUは、関数全体としては非線形でしたが、正の領域や負の領域に限定すると線形性をもっていました。eLUは負の領域で指数関数を適用します。
| $$ elu(x) = \left\{\begin{array}{ll} x&(x\geq 0)\\ e^x-1&(x<0) \end{array}\right. $$ |
| $$ \frac{d}{d x}elu(x) = \left\{\begin{array}{ll} 1&(x\geq 0)\\ e^x&(x<0) \end{array}\right. $$ |
elu = lambda x: np.where(x > 0, x, np.exp(x)-1) # eLU
elu_der = lambda x: np.where(x > 0, 1, np.exp(x)) # eLUの導関数Scaled eLU(SeLU)
| $$ Selu(x) = \lambda \left\{\begin{array}{ll} x&(x\geq 0)\\ \alpha (e^x-1)&(x<0) \end{array}\right. $$ 以下のグラフでは、\(\lambda =0.5, \alpha =8\)としたときの例です。 |
| $$ \frac{d}{d x}Selu(x) = \lambda \left\{\begin{array}{ll} 1&(x\geq 0)\\ \alpha e^x&(x<0) \end{array}\right. $$ |
selu = lambda x, lam, a: lam * np.where(x > 0, x, a*(np.exp(x)-1)) # SeLU
selu_der = lambda x, lam, a: lam * np.where(x > 0, 1, a*np.exp(x)) # SeLUの導関数Swish
Swishと同じようなものに、Sigmoid-Weighted Linear Unit(SiLU)というものがあり、これもReLUファミリーと考えることができます。
| $$ swish(x) = x\cdot sigmoid(\beta x) $$ |
| $$ \frac{d}{d x}swish(x) = \beta\cdot swish(x) + sigmoid(\beta x)\cdot (1-\beta\cdot swish(x)) $$ |
swish = lambda x, beta=1: x*sigmoid(beta*x) # Swish関数
swish_der = lambda x, beta=1: beta*swish(x) + sigmoid(beta*x)*(1-beta*swish(x)) # Swishの導関数Mish
| $$ mish(x) = x\cdot tanh((softplus(x))) $$ |
| $$\frac{d}{d x}mish(x) = tanh((softplus(x)))+x(1-tanh((softplus(x)))^2)\cdot sigmoid(x)$$ |
mish = lambda x: x*tanh(softplus(x))
mish_der = lambda x: tanh(softplus(x)) + x*(1-tanh(softplus(x))**2)*sigmoid(x)最後に
ここに示した活性化関数はほんの一部で、本当に多くのバリエーションがあります。ここでは、活性化関数を覚えるというよりは、誤差逆伝播の関連性も含めて、どういう背景で何を実現したくて考案されたのかな?っていう部分に重点を置いて観察したときに何か知見が得られれば、本記事の目標達成かなと思っています。
