4脚ロボットの歩行において、足先の軌道生成はとても重要な一方で、難しくて分かりにくい領域の1つです。気軽に足先の軌道を生成させてみたくても、ROSを使う必要があったり、複雑な学術的な研究のソースコードを見る必要があったりと、ハードルが高かったのが現状です。そこで、気軽に足先の軌道生成を試せるようにライブラリを作成したので紹介します。
作成したライブラリは、以下のリポジトリで公開しています。

概要
開発したライブラリ名は「Foot Trajectory」です。現時点では、以下の3つの軌道生成器をサポートしています。
- スプライン軌跡
- サイン軌跡
- ベジェ軌跡
4脚ロボットに実装で使えることを目指しています。同時に開発者にとっても使いやすいように、軌道の可視化機能も提供しています。
各々の軌道生成器について
各軌道生成器で必要な専門的内容は、ここでは避け、要点だけ記載します。
スプライン軌道
スプライン軌道とは、スプライン補完に基づく軌道です。論文「Learning Quadrupedal Locomotion over Challenging Terrain」で紹介さ入れているスプライン軌道の式に基づき、一部変更して作成しました。ライブラリに実装したスプライン軌道は以下の通りです。
$$
F(\phi_i) = \left\{\begin{array}{ll}
h(-2k^3+3k^2) & 0 \le k < 1\\
h(2k^3-9k^2+12k-4) & 1 \le k < 2\\
0 & \text{otherwise}
\end{array}\right.
$$
ここで\(k\)は\(\frac{2(\phi_i - \pi)}{\pi}\)で、ラジアン表記の角度情報\(\phi_i\)(\(i\)は脚の番号)を-2から2の間に変換する関数です。\(k\)の値の範囲に応じて場合分けします。\(h\)は高さを表します。
この軌道を、高さと幅を変えて3パターン描画したものを下図に示します。
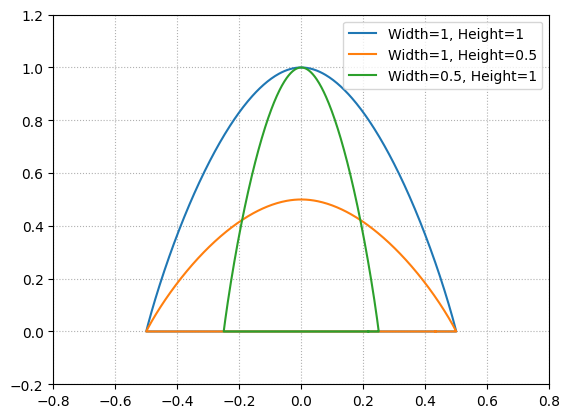
計算式を以下に示します。以下の\((x(t), y(t))\)を描画することになります。
$$
x(t) = \frac{w}{2} \cos(\phi(t))
$$
$$
y(t) =
\begin{cases}
h (-2k^3 + 3k^2), & 0 \le k < 1 \\
h (2k^3 - 9k^2 + 12k - 4), & 1 \le k < 2 \\
0, & otherwise
\end{cases}
$$
$$
\phi(t) = \text{mod}(\phi_0 + 2\pi(f + f_\text{offset})t, 2\pi)
$$
$$
k(t) = 2 \left( \frac{\phi(t) - \pi}{\pi} \right)
$$
サイン軌道
サイン軌道については、スウィングフェーズに\(\sin\)関数を用いたものです。
先ほどと同様に、高さと幅を変えて3パターン描画したものを下図に示します。
正弦関数は円の回転から求まる通り、とても丸っこい軌道になります。
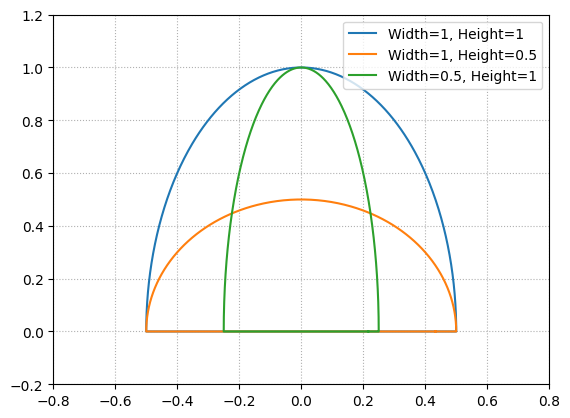
計算式を以下に示します。以下の\((x(t), y(t))\)を描画することになります。
$$
x(t) = \frac{w}{2} \cos(\phi(t))
$$
$$
y(t) =
\begin{cases}
0, & 0 \le \phi(t) < \pi \\
h \sin(\phi(t) - \pi), & \pi \le \phi(t) < 2\pi
\end{cases}
$$
$$
\phi(t) = \text{mod}(\phi_0 + 2\pi(f + f_\text{offset})t, 2\pi)
$$
ベジェ軌道
ベジェ軌道とは、ベジェ補完に基づく軌道です。論文「Leg Trajectory Planning for Quadruped Robots with High-Speed Trot Gait」で紹介さ入れているベジェ軌道を実装しました。
※スタンスフェーズは論文と異なる可能性があります。
ベジェ軌道を作成するときは、ベジェ軌道を生成するための制御点を複数用意し、それをベジェ補完することで得ます。
実装したベジェ軌道を生成するときに使用する制御店は以下の通りです。
DESIRED_VELOCITY = 10
SWING_PERIOD = 1
POINTS_COUNT = 11
CONTROL_POINTS = np.array([
[-0.5, 0],
[-(0.5 + DESIRED_VELOCITY / ((POINTS_COUNT + 1) * SWING_PERIOD) / 340), 0],
[-0.88, 0.73],
[-0.88, 0.73],
[-0.88, 0.73],
[0, 0.73],
[0, 0.73],
[0, 1],
[0.88,1],
[0.88, 1],
[0.5 + DESIRED_VELOCITY / ((POINTS_COUNT + 1) * SWING_PERIOD) / 340, 0],
[0.5, 0]
])ベジェ補完の式は以下の通りです。
$$
B(t) = \sum_{i=0}^n {}_nC_i P_i (1-t)^{n-i}t^i
$$
先ほどと同様に、高さと幅を変えて3パターン描画したものを下図に示します。
ベジェ補完は、スプライン補完やサイン補完と異なり、スウィングとスタンスがスムーズに結ばれているのが特徴です。
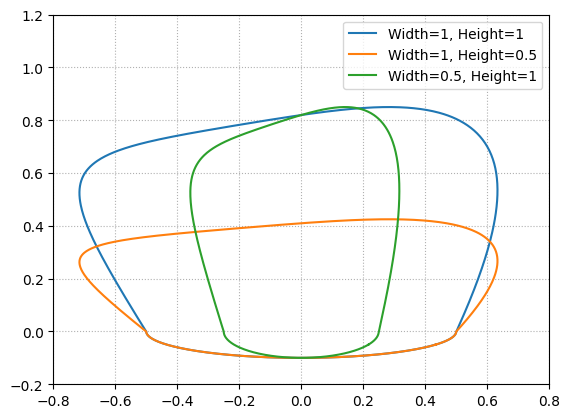
計算式を以下に示します。以下の\((x(t), y(t))\)を描画することになります。
$$
x(t) = \frac{w}{2} \cos(\phi(t))
$$
$$
y(t) =
\begin{cases}
-0.1h \sin(\phi(t)), & 0 \le \phi(t) < \pi \\
h B(\phi(t) - \pi), & \pi \le \phi(t) < 2\pi
\end{cases}
$$
$$
\phi(t) = \text{mod}(\phi_0 + 2\pi(f + f_\text{offset})t, 2\pi)
$$
$$
B(t) = \sum_{i=0}^{n} {}_nC_i (1-t)^{n-i} t^i P_i
$$
ライブラリのインストール方法
以下のコマンドを実行することでインストールすることができます。
pip install git+https://github.com/aakmsk/foot_trajectory.git軌道クラスの使い方
使い方の大まかな流れは、①軌道クラスのインスタンス化、②compute_trajectoryメソッドの実行です。
使用したい軌道クラス(SplineFootTrajectoryGenerator、SineFootTrajectoryGenerator、BezierFootTrajectoryGenerator)をインポートしてください。
import numpy as np
from foot_trajectory.foot_trajectory import (
SplineFootTrajectoryGenerator,
SineFootTrajectoryGenerator,
BezierFootTrajectoryGenerator
)軌道生成器のインスタンス化と、軌道の生成を行います。今回は、軌道生成(compute_trajectory)において時刻tを配列にしていますが、リアルタイムに生成させたい場合は、プログラムの経過時間などのスカラーを入力します。
spline_generator = SplineFootTrajectoryGenerator(base_frequency=1.0, initial_phi=0.0)
sine_generator = SineFootTrajectoryGenerator(base_frequency=1.0, initial_phi=0.0)
bezier_generator = BezierFootTrajectoryGenerator(base_frequency=1.0, initial_phi=0.0)
t = np.linspace(0, 2 * np.pi, 100)
spline_trajectory = spline_generator.compute_trajectory(t, frequency_offset=0, width=1, height=1)
sine_trajectory = sine_generator.compute_trajectory(t, frequency_offset=0, width=1, height=1)
bezier_trajectory = bezier_generator.compute_trajectory(t, frequency_offset=0, width=1, height=1) インスタンス化の際の引数には、base_frequencyとinitial_phiがあり、前者は軌道の周波数を、後者は時刻0の時の軌道位置(すなわち軌道生成器のスタート位置)を表します。base_frequency=1にすれば、1秒でスウィングとスタンスの一連の動作を実行します。base_frequency=0.2にすれば、周期と周波数の公式\(T=1/f\)より5秒かけて実施します。つまり、歩行速度を変更できるのです。initial_phiについては、指定する値と、そのスタート位置を下図に示します。
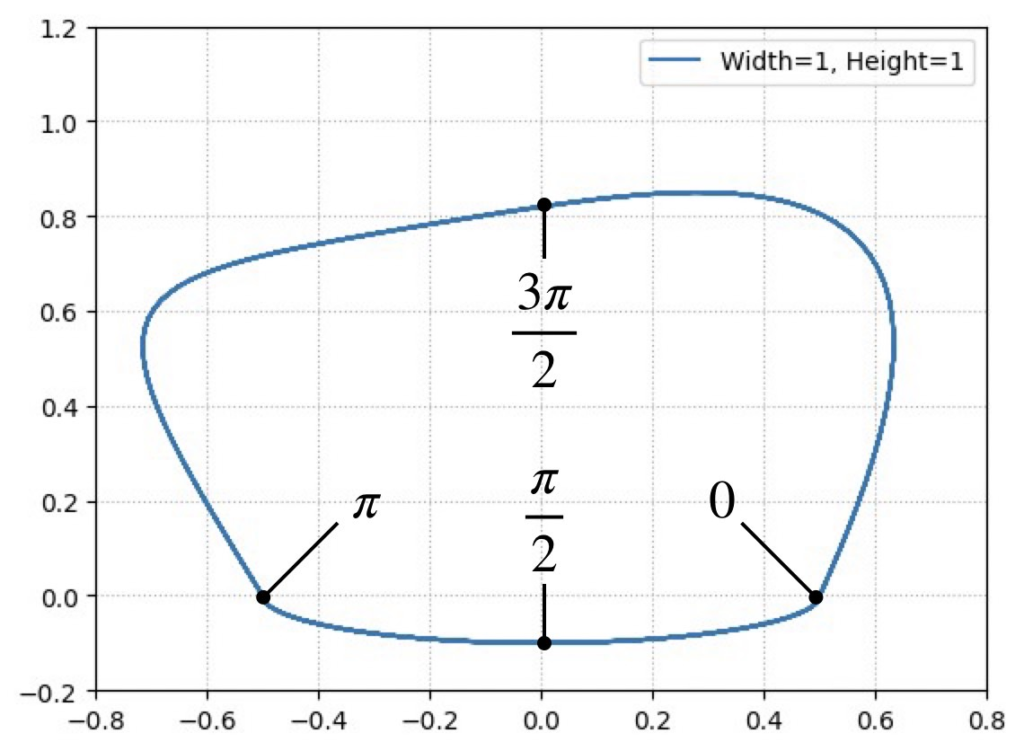
\(0\rightarrow\frac{\pi}{2}\rightarrow\pi\):スタンス
\(\pi\rightarrow\frac{3\pi}{2}\rightarrow 2\pi(0)\):スウィング
つまり、initial_phi=0のときはスタンス動作から始まり、initial_phi=np.piとすればスウィングから始まります。
compute_trajectoryの引数には、t、frequency_offset、width、heightがあります。順番に、取得したい軌道の時刻、オフセット周波数、幅、高さです。オフセット周波数は基本的に0にしておけばよいですが、一時的に回転速度を上げたい場合や下げたい場合に使用することができます。幅や高さは、軌道の幅と高さを表します。width=1、height=1の場合、軌道の幅や高さは1です(ベジェ軌道の場合は誤width=1はスタンス長)。サイズや単位は、使用される環境に合わせてください。
可視化ツールの使い方
現時点では、可視化ツールとして、アニメーション化の機能を用意しています。アニメーション化の機能は以下のようにしてインポートします。
from foot_trajectory.foot_trajectory import TrajectoryAnimationアニメーションは次のようにして作成します。
animation = TrajectoryAnimation(
t, # 軌道生成で使用した時刻(s)の配列
spline_trajectory, # 描画したい軌道情報
save_name="spline_trajectory.mp4", # 保存名を指定
axis_limits=(-1, 1, -0.5, 1.5) # 描画範囲を指定
)width=1、height=1として、それぞれの軌道生成器で生成された軌道を可視化すると次のようになります。可視化した軌道の周波数は、全て1Hzです。
※TrajectoryAnimationの引数として軌道生成時の時刻配列を渡しているのは、アニメーション化の際に動作速度を正確に再現するためです。また、mp4であれば動作速度はおおむね正確ですが、gifの場合は動作速度は全く参考になりませんので注意してください。
スプライン軌道の動作例です。
サイン軌道の生成例です。
ベジェ軌道の生成例です。
説明は以上になります。
今後、ライブラリを更新したら追記します。
