本記事では、sklearnのMLPClassifierを使用して簡単に深層学習を体験してみることに重点をおいて解説していきたいと思います。
当サイトはTwitterやYouTubeでも情報発信しています。ご気軽にフォロー(@AGIRobots)、チャンネル登録お願いします!
動画でも本記事の内容を解説しているので、ぜひご視聴ください~。
MLPClassifierとは
MLPClassifierはMulti-layer Perceptron classifierの略で、多層パーセプトロンとよばれる分類器のモデルです。多層パーセプトロンとは、ディープラーニングで使用されるニューラルネットワークで、ディープニューラルネットワークとも呼ばれます。モデルを学習するには学習の指標となる目的関数を定める必要があります。多層パーセプトロンは回帰問題や分類問題の両方に使用でき、sklearnのMLPRegressionとMLPClassifierがそれぞれ対応します。本記事で扱うMLPClassifierは分類問題を扱うため交差エントロピー誤差関数を目的関数として使用し、交差エントロピー誤差関数を最適化する(目的関数をいかにして小さくしていくか)ためのテクニックとしてL-BFGS*1準ニュートン法に属すBFGS法の一種または確率的勾配降下法を使用します。
少し専門用語が出てきて、混乱しかけた方もいるかもしれませんが、以降では使い方を紹介していきたいと思います。
手書き数字認識モデルをつくってみる
MNISTとよばれるデータセットについてご存じのない方に向けて簡単に紹介すると、人間が手書きした28x28ピクセルの0から9のモノクロ数字画像とそのラベルが格納されたデータの集合で、訓練用データが60000枚、テスト用データが10000枚あります。
今回は、このMNISTデータセットとsklearnのMLPClassifierを使用して簡単な手書き数字認識ができる深層学習モデルを作成していきます。
MNISTデータセットを読み込んで訓練データとテストデータに分ける
先ほど、MNISTデータセットは、訓練用データが60000枚、テスト用データが10000枚あると紹介しました。なぜ2つに分けるか少し解説しておくと、学習したモデルの汎用性を客観的に計測するためです。例えば、大学の定期試験で授業中に扱ったものと全く同じ問が出題されれば本質を理解していなくても大抵は解答できますよね。しかし、それでは本当に理解しているかどうか測るのは難しいので、初めて見た問が出題されたりするわけです。同じ問題なら正しく理解しようとしなくても記憶だけで何とかなってしまいます。機械学習モデルも同様で、特に大規模なニューラルネットワークですと、学習データを完全に丸暗記することぐらいは容易にこなしてしまいます。しかし、その場合は汎化性能がとても低く全くといっていいほど使い物になりません。ですので、客観的に計測するデータが必要になるわけです。ここで使用されるのがテストデータです。
ここではMNISTデータセットの利用を通じて体験していただければと思います。
MNISTデータセットを読み込む手法はいくつかありますが、ここでは深層学習で頻繁に使用されるKerasというライブラリを使って読み込んでみたいと思います。
from keras.datasets import mnist
from keras import utils #OneHot表現に変更する関数
(x_train, y_train), (x_test, y_test) = mnist.load_data()上のコードでは、mnistを読み込むための関数のほか、utilsクラスを読み込んでいますが、分類問題では0から9の手書き数字の値を学習するのではなく(この場合は回帰問題)、出力層に0から9の手書き数字クラスに対応する専用ニューロンを用意することで対応し、このときの教師信号はOneHotベクトル表記と呼ばれる形状である必要があります。先ほどデータセットを読み込んだままの状態では、教師データがOneHotベクトル表記になっていないので、utils関数のto_categoricalメソッドを使って変換します。
Y_train = utils.to_categorical(y_train, 10)
Y_test = utils.to_categorical(y_test, 10)また、ニューラルネットワークに入力する数値は、正規化もしくは標準化されたものが相応しいので、ここでは、255で正規化することにします。
X_train = x_train.reshape(60000, 784) / 255
X_test = x_test.reshape(10000, 784) / 255以上で訓練用のデータ(入力:X_train、教師信号:Y_train)、テスト用のデータ(入力:X_test、正解ラベル:Y_test)の利用準備ができました。
モデルを学習させる
実際にMLPClassifierを使用してディープニューラルネットワークを定義し、深層学習の体験をしてみたいと思います。学習の進捗状況などはhistoryに記録させます。
mlpclf = MLPClassifier(hidden_layer_sizes=(100, 100, 100), activation='relu', verbose=True, warm_start=True)
history = mlpclf.fit(X_train, Y_train)historyに記録された各イテレーションごとの進捗状況の一部の例を以下に載せます。
Iteration 1, loss = 1.09724523
Iteration 2, loss = 0.32702274
Iteration 3, loss = 0.22946111
...
Iteration 47, loss = 0.00765463
Iteration 48, loss = 0.00445658
Iteration 49, loss = 0.00384859
training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.モデルを評価する
テスト用データを使ってモデルの出力の正解率を計算してみます。
y_proba = mlpclf.predict_proba(X_test) #mlpclf.predict(X_test)でもOK
y_esti = np.argmax(y_proba, 1)
y_real = np.argmax(Y_test, 1)
acc = np.sum(y_esti == y_real)/len(y_esti)
print(str(acc) + '%')結果、正解率は0.9757%となりました。上記のコードは割と真面目に定義通り求めていますが、実は正解率をもっと簡単に求める方法が用意されています。ページの後半に付録として記載してるリファレンスを参照いただければと思いますが、scoreメソッドを使う方法です。
mlpclf.score(X_test, Y_test)これを実行すれば、そのまま先ほどと同じ結果を得ることができます。
モデルの評価は正解率を見るだけではなく、誤差関数(目的関数)の変化を可視化してみることも大切です。誤差関数の変化を可視化することで、どこから過学習が発生しているかなど検討をつけることができます。
plt.plot(history.loss_curve_)
plt.xlabel('Iteration')
plt.ylabel('loss')
plt.grid(True)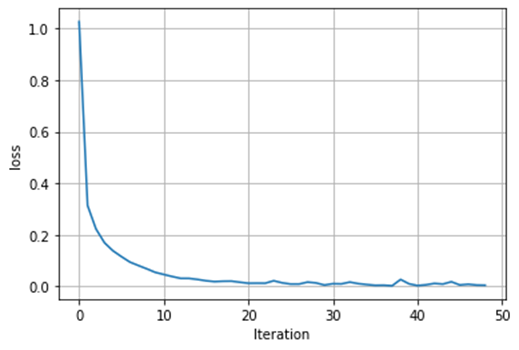
誤差関数はとてもきれいに収束していることが分かります。
まとめ
どちらかというと古典的な機械学習モデルが中心的で、事前学習で使用されるイメージがあるscikit-learnですが、そこに取り入れられた深層学習クラスのMLPClassifierはとても簡単にディープラーニングを実行できることがお分かりいただけたと思います。一方で、個々のパラメータ設定は柔軟性に欠けているのが現実ではないかと個人的に感じております。もちろん、MLPClassifierで事足りるなら問題ないですが、事足りない学習対象であっても、深層学習がどの程度その学習対象に有用なのか、確かめるときに使いやすい便利なクラスでした。
これ以降の内容は、MLPClassifierに関わるパラメータやメソッドのリファレンスです。必要に応じて参照してみてください。
リファレンス
MLPClassifierのパラメータ
MLPClassifierではパラメータとして何が設定できるのか覗いてみます。
MLPClassifier(
hidden_layer_sizes=(100,),
activation='relu',
solver='adam',
alpha=0.0001,
batch_size='auto',
learning_rate='constant',
learning_rate_init=0.001,
power_t=0.5,
max_iter=200,
shuffle=True,
random_state=None,
tol=0.0001,
verbose=False,
warm_start=False,
momentum=0.9,
nesterovs_momentum=True,
early_stopping=False,
validation_fraction=0.1,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-08,
n_iter_no_change=10,
)
このように、22個のパラメータを引数として受け取ることができます。では、個々に説明していきます。
hidden_layer_sizes
デフォルト値:hidden_layer_sizes=(100,)
中間層のサイズを設定します。デフォルトでは、ニューロンを100個もつ中間層が1つのみに定義されています。つまり、図1のような三層ニューラルネットワークです。

です。
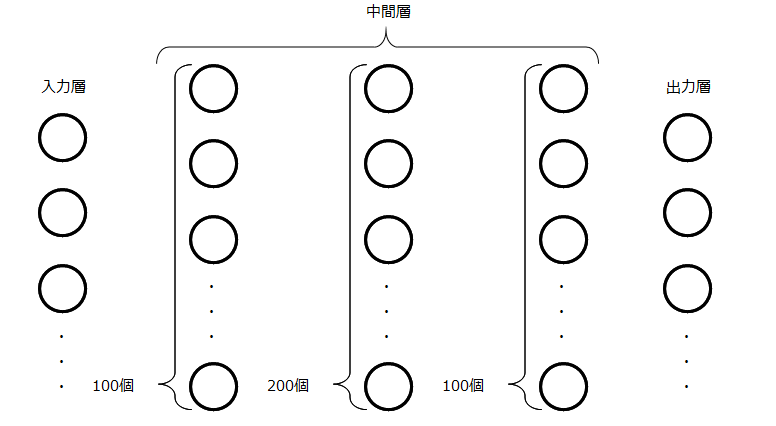
中間層が3つ(各中間層のニューロン数が100個、200個、100個)の5層ニューラルネットワークを設定したいときは、
hidden_layer_sizes=(100, 200, 100)
のように記述します。
activation
デフォルト値:activation='relu'
中間層の活性化関数を設定します。デフォルトでは、ランプ関数(ReLU)が設定されています。引数として渡せる活性化関数は以下の4種類です。
・identity:恒等関数( \(f(x) = x\) )
・logistic:シグモイド関数(\(f(x) = \frac{1}{1 + e^{-x}}\) )
・tanh:双曲線正接関数
・relu:ランプ関数(\(f(x) = max(0, x)\) )
問題点は、中間層の層ごとに活性化関数を違うものにできないことです。いくら層を深くしても、設定できる活性化関数の種類は1つのみです。
solver
デフォルト値:solver='adam'
重みの最適化手法を設定します。ここで設定できる最適化手法は、
・lbfgs:準ニュートン法に属すBFGSの一種
・sgd:確率的勾配降下法
・adam:確率的勾配降下法にモーメントなる動きをつけたもので現在の主流
比較的大きなデータセットではadamを、小さなデータセットではlbfgsを設定するとうまくいくことが知られています。
alpha
デフォルト値: alpha=0.0001
L2正則化項が誤差関数に与える影響の大きさを調節する正則化パラメータです。過学習に陥るときは、小さな入力値の変化で出力値が大きく変化する状態で、重みベクトルのユークリッドノルムが大きいことが知られています。そのため、重みベクトルのユークリッドノルムが大きくならないように、L2正則化項を追加し、それが与える影響を調節します。
batch_size
デフォルト値:batch_size='auto'
最適化時のバッチサイズを決めます。デフォルトではautoに設定されています。autoの場合、batch_size=min(200, n_samples)、つまり、バッチサイズは最も多くて200です。最適化手法としてL-BFGSを使用した場合、ミニバッチを使用しません。
learning_rate
デフォルト値:learning_rate='constant'
学習率の変化を設定します。学習率は、引数learning_rate_initに渡しましが、デフォルトでは、それが定数として設定されています。設定できるのは、
・constant:学習率は定数です。
・invscaling:effective_learning_rate = learning_rate_init / pow(t, power_t) のように、時間とともに学習率が小さくなります。ここで、power_tはtの指数部です。pow(x, y)はxのy乗を返す関数なので、 pow(t, power_t)は、\(t^{power_t}\)となり、学習率が、時間の累乗に反比例して小さくなります。
・adaptive:誤差関数が減少し続ける限り、学習率を一定に保ちます。しかし、2回連続するepochで、訓練誤差が最低でもtolより減少しなかった場合と、検証スコアが上昇が少なくともtolより上昇しなかった場合に、現在の学習率を5で割ったものに更新します。
learning_rate_init
デフォルト値:learning_rate_init=0.001
学習率を設定します。これは、最適化手法としてSGDかadamが選ばれたときにのみ使用されます。
power_t
デフォルト値:power_t=0.5
learning_rateの'invscaling'において、時間tの指数部を設定します。この値が大きいと、学習率が急速に小さくなります。これは、SGDが最適化手法として選ばれたときのみ使用されます。
max_iter
デフォルト値:max_iter=200
エポック数を指定します。デフォルトではエポックが最大で200に設定されています。途中で打ち切りが生じる場合を考慮すると、すべてのエポックが最後まで実行されるとは限りません。
shuffle
デフォルト値:shuffle=True
学習時のサンプルを毎回シャッフルするかどうかを設定します。SGDとAdamの場合にのみ使用されます。
random_state
デフォルト値:random_state=None
基本的にはランダム値のシードを設定します。しかし、整数を入力した場合は、random_stateはシードを表します。一方で、RandamStateのインスタンスを入力した場合、random_stateは乱数ジェネレータになります。デフォルトのNoneではnp.randomによるRandomStateのインスタンスが使用されます。
tol
デフォルト値:tol=0.0001
学習がある程度進んだところで、学習率を変化させたり打ち切らせるときに、使用されるパラメータです。
verbose
デフォルト値:verbose=False
学習途中の進捗状況を標準出力に出力するかどうか設定します。
warm_start
デフォルト値:warm_start=False
学習を何度も行いたいとき、つまり、fitを何度も呼び出すときに、呼び出す以前に行った重みを引き継ぐかどうかを設定します。
momentum
デフォルト値:momentum=0.9
勾配降下法による学習時にモーメンタムをどの程度反映させるかを0~1の間で設定します。
nesterovs_momentum
デフォルト値:nesterovs_momentum=True
モーメンタム法の一種である、Nesterovの加速法を有効化するかどうかを設定します。
early_stopping
デフォルト値:early_stopping=False
学習を途中で打ち切るかどうかを設定します。
validation_fraction
デフォルト値:validation_fraction=0.1
上のearly_stoppingがTrueのとき、早く打ち切るかどうかを判断するために使用される検証用データの割合を設定します。
beta_1
デフォルト値:beta_1=0.9
Adamで使用します。
beta_2
デフォルト値:beta_2=0.999
Adamで使用します。
epsilon
デフォルト値:epsilon=1e-08
Adamで使用します。
n_iter_no_change
デフォルト値:n_iter_no_change=10
tolの条件を満たさないエポックの最大数を設定します。
MLPClassifierのメソッド
驚くべきことに、ほとんどのパラメータがあらかじめ設定されていることが分かります。主にこちらで設定すべき項目は
・hidden_layer_sizes:各層のニューロン数
・activation:活性化関数
・max_iter:エポック数
・verbose:学習の進捗の表示の有無
・warm_start:fitを実行するときに重みを引き継ぐかどうか
でしょう。では、中間層が3層(各層のニューロン数は100個とする)で、活性化関数を全てrelu、学習の進捗状況を表示させ、重みを引き継がせたい場合を考えてみましょう。このとき、
mlpclf = MLPClassifier(hidden_layer_sizes=(100, 100, 100), activation='relu', verbose=True, warm_start=True)
のようにインスタンス化します。この後、このインスタンスに対してメソッドを使用して学習、予測、正解率などを計算していきます。各メソッドについて説明します。
predict_proba()
array_likeかmatrixである入力を受けます。形は(n_samples, n_features)です。つまり、個々の入力データは行ベクトルです。出力はarray-likeで形は(n_samples, n_classes)です。各クラスに属する確率を出力します。
set_params()
略。
fit()
入力Xをarray_likeまたは行列(n_samples, n_features)、教師データyをarray-likeまたは行列、つまり (n_samples,) または (n_samples, n_outputs)とします。このとき、mlpclf.fit(X, y)のように、モデルのトレーニングを行います。
predict()
array_likeかmatrixである入力を受けます。形は(n_samples, n_features)です。つまり、個々の入力データは行ベクトルです。出力はarray-likeで形は(n_samples, n_classes)です。推定されるクラスのみ1になります。
get_params()
パラメータが確認できます。例えば、
{'activation': 'relu',
'alpha': 0.0001,
'batch_size': 'auto',
...
'validation_fraction': 0.1,
'verbose': True,
'warm_start': True}
が取得できます。
predict_log_proba()
略。
score()
テスト用データとテスト用教師データを入力することで、正解率を簡単に得ることができます。例えば
score(X, y)
のように使用します。
References
| ↲1 | 準ニュートン法に属すBFGS法の一種 |
|---|
