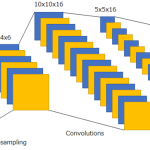
畳み込みニューラルネットワーク(CNN)はディープラーニングの中心的な存在です。また、CNNは脳科学的な観点から見ても、わりと早いうちから機能や構造が明らかになっていた視覚野や網膜の情報処理と強い関係があります。近年は、深層学習技術が先導していますが、その背後には生物で行われている情報処理のメカニズムとは切っても切れないような関係にあると思います。ですので、本記事では網膜や視覚野の情報処理から触れて、畳み込みニューラルネットワークを概観したいと思います。
前半は生物の情報処理に関わる内容を扱っていますが、中間では自己組織化マップを実際にコーディングしたりしています。また、以下の記事では、本記事よりも畳み込みニューラルネットワークの演算に力を入れて解説しているので、もしよければ以下の記事も合わせて読んでいただければと思います。
レジュメ
畳み込みニューラルネットワークは視覚野や網膜の情報処理構造ととても大きな関係性があります。また、畳み込みニューラルネットワークに関わらずではありますが、多くの深層学習モデルは目的関数を定めたうえ、誤差逆伝播による教師あり学習により学習を進めます。一方で、生体では自己組織化による学習が行われていたりします。畳み込みニューラルネットワークの元となったネオコグニトロンといわれる視覚野のモデルは自己組織化により学習をおこないます。現在の畳み込みニューラルネットワークに比べ生体の情報処理に近いシステムをとっている点は大変興味深い話です。これらの分野について大まかに扱ったうえで、最後にLeNetの紹介ができればと思います。
網膜・視覚野の情報処理
まず始めに、畳み込みニューラルネットワーク(以下CNN)のネットワーク構造と網膜や視覚野の神経ネットワーク構造がいかに似ていて、また、模倣されているのか理解していただくために、ここでは、網膜と視覚野の情報処理について解説していきます。
網膜について
まず先に、なぜ網膜の情報処理から学ぶのか説明すると、人間の網膜は本来であれば視覚野で行われてもおかしくない情報処理の一部を担っているためです。人間の網膜はCCDやCMOSなどのイメージセンサに対応するという例えは、あながち間違っていませんが、厳密にいうと機能として異なります。イメージセンサは実世界を2次元平面世界の幾何に写像する機能をもっていますが、網膜はイメージセンサの機能+画像処理を行っています。この画像処理という部分が重要で、ここのテーマになります。余談ですが、全ての動物の網膜で画像処理を行っているわけではありません。画像処理を行えるのは、人間などの脊椎動物の網膜であり、タコの網膜は当にイメージセンサの機能しか持っていないといっても差し支えないでしょう。
話を戻しますが、画像処理を行える網膜はどのような構造をしているのか気になりませんか?
これについて説明していきたいと思います。
人間の眼の網膜構造
図1は人間の眼の網膜の構造を表しています。人間の眼の網膜には光を感知する細胞(これを視細胞という)として桿体細胞、赤錐体、青錐体、緑錐体の4種類が存在します。人間は3色型色覚なので3種類の錐体細胞がありますが、犬猫のように2色型色覚の動物や、鳥のように4色型色覚の動物もいます。以降では人間の眼の網膜に限定して話を進め、網膜といえば人間の眼の網膜を指すものとします。
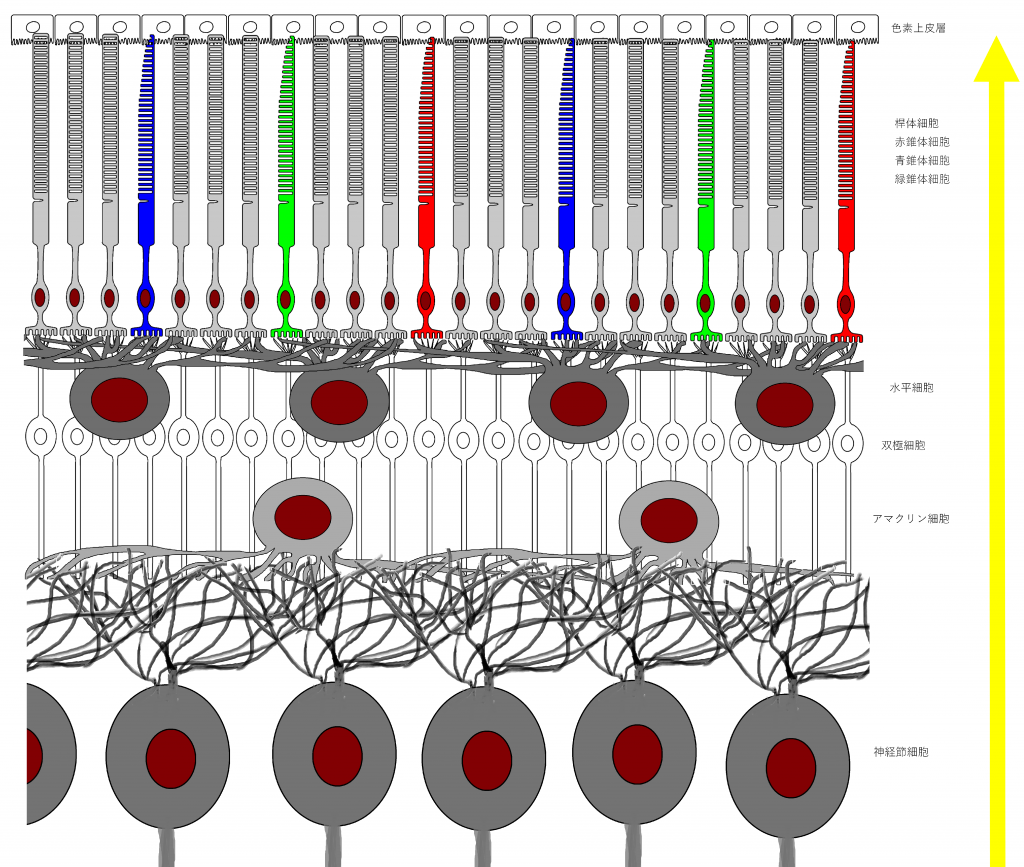
図1において、網膜のグリア細胞であるミュラー細胞*1網膜細胞の維持管理に関与していると考えられる。また、視細胞に分化したという報告もある。脳のグリア細胞(アストロサイト、オリゴデンドロサイト、シュワン細胞など)は情報処理に関与していることが明らかになりつつあり、ミュラー細胞が今後注目される可能性は否定できない。は省略しています。
図1には上(網膜の奥側)から順に、色素上皮細胞、視細胞、水平細胞、双極細胞、アマクリン細胞、神経節細胞が描かれています。色素上皮細胞*2網膜内の余計な光を吸収し、散乱を防いでいる。は除き、それぞれの細胞について、分かりやすく図2として表にしました。
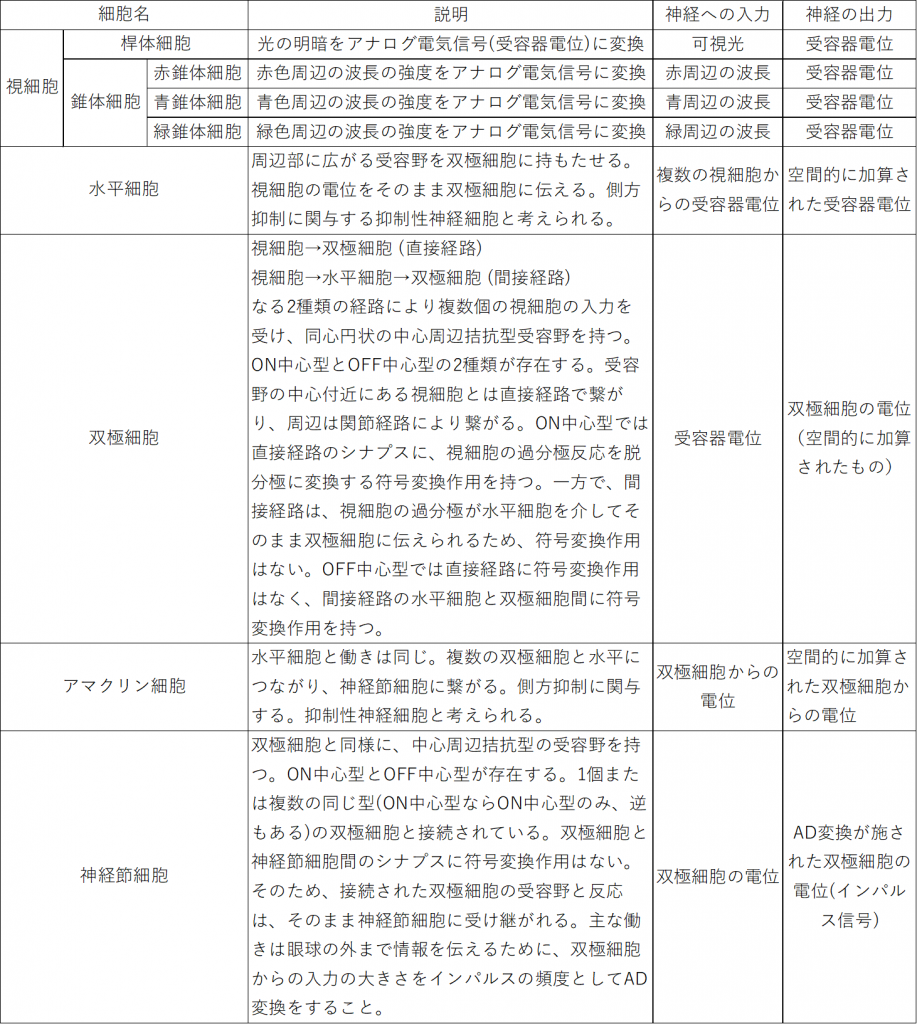
フォトダイオードの役割を果たす視細胞は、桿錐体層を成しており、これがイメージセンサに対応する働きをしています。その内側の層には、水平細胞、双極細胞、アマクリン細胞、神経節細胞が分布し、タコが脳(正確には視葉)で行っている処理、いわゆる画像処理を行います。
視細胞による光の電気信号(受容器電位)への変換
ここでは、イメージセンサを構成するフォトダイオードが光信号を電気信号に変換するように、視細胞が光刺激を電気信号に変換するメカニズムについて簡単に紹介します。
視細胞は光刺激を受け取ると受容器電位は視細胞に光が当たることで発生する膜電位で、光の当たり方により、変化が異なります。主にフラッシュ光と連続光の場合で、分けて
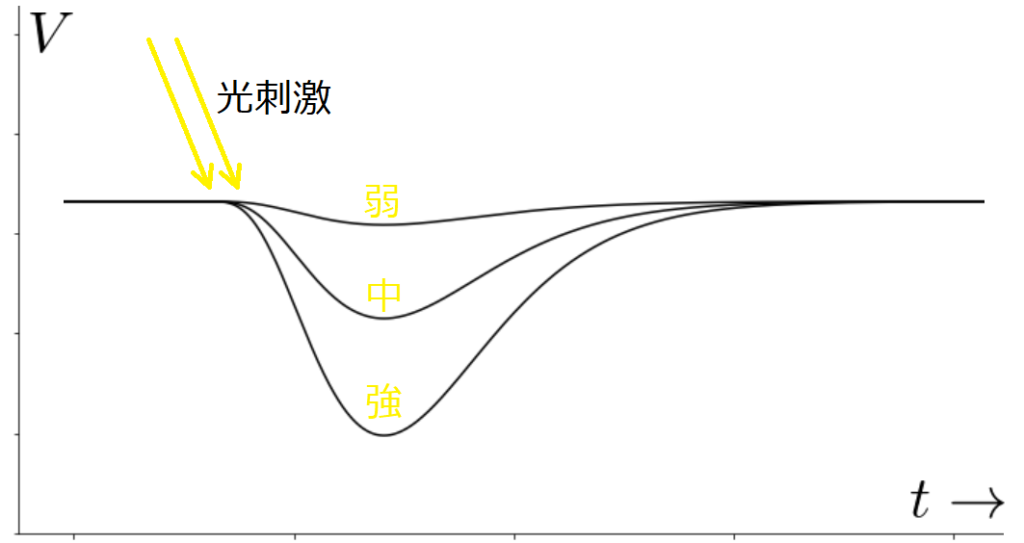
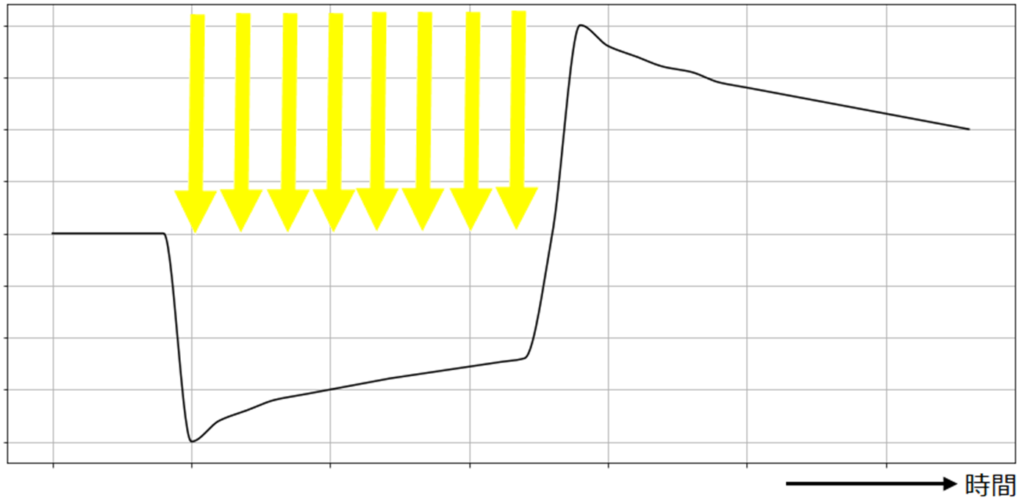
図3のように、インパルス的なフラッシュ光があたると、光の強さに応じた電位が現れます。一方で、図4のような持続的な光に対してはコンデンサのように時間的な微分作用をもつ変化をします。
中心周辺拮抗型受容野
ここでは、網膜や視覚経路だけでなく感覚系で中心的に扱われている受容野構造をについて紹介しておきたいと思います。まず受容野とは感覚系ニューロンに活動の変化を起こすことが可能な空間的領域のことをいいます。この受容野には様々な形状があり、その1つが中心周辺拮抗型です。中心部分と周辺部分が真逆の反応を示す特性を持っていて、電気的な話でいえば、正か負のどちらの影響を与えるかということになりますが、その変化を与える光刺激は、補色関係にある組み合わせになっています。図5にそのイメージを示します。
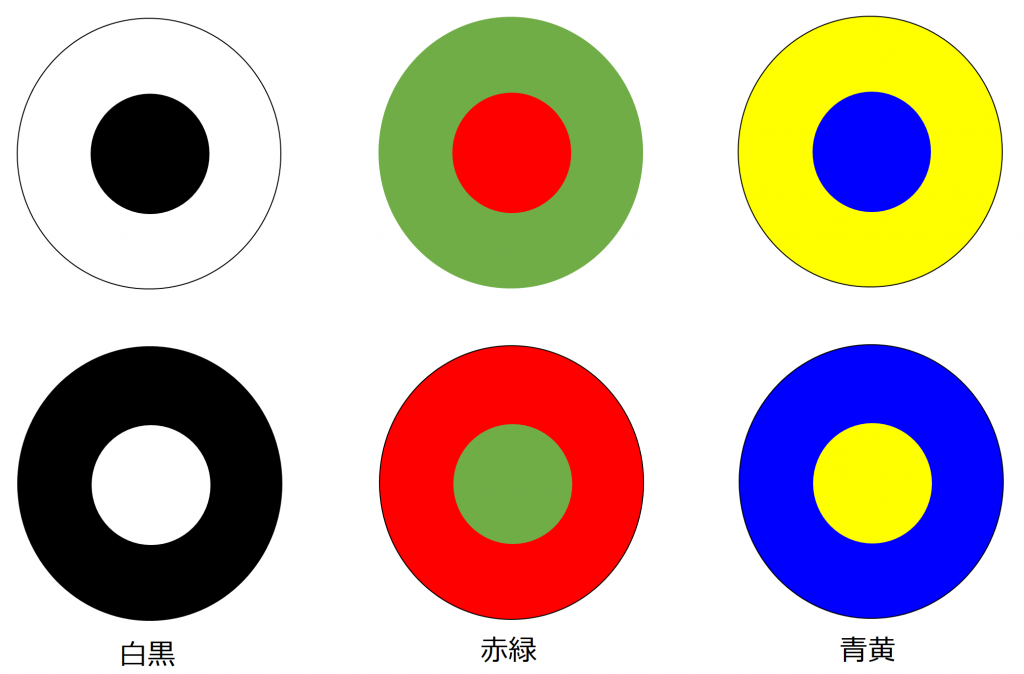
補色関係にある色同士は、互いの色が最も強調される組み合わせになっていて、網膜の神経ネットワークでは白と黒、赤と緑、青と黄の組み合わせに最も強く反応を示します。また、それぞれにはON中心型とOFF中心型があります(例:白が中心か黒が中心か)。
白と黒の受容野は、 明暗を認識する桿体細胞を入力とするネットワークにより実現できます。赤と緑の受容野は赤と緑の錐体細胞を入力として受けるネットワークにより実現できます。青と黄は、黄色を単体で認識する細胞がないため注意が必要ですが、黄は赤と緑の混色として実現できるので、3つの錐体細胞からの入力を受けるネットワークにより実現できます。
余談ですが、視覚情報処理系で中心周辺拮抗型の受容野が使用されるのは、双極細胞を起点とし、神経節細胞、外側膝状体、一次視覚野と伝わる経路です。
シナプスにおける符号変換作用
シナプスによる符号変換作用とは、シナプスにおいてプラスの刺激をマイナスの刺激に変換することです。なぜこのような仕組みが必要かというと、さきほど示した中心と周辺が逆の刺激として入力されることで実現される受容野を実現できるようにするためです。
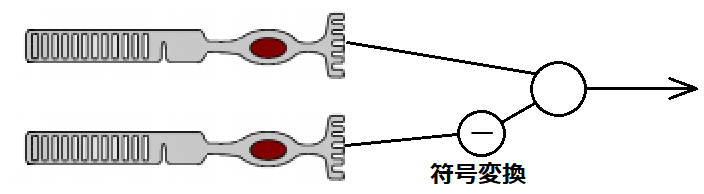
網膜では、双極細胞が視細胞から中心周辺拮抗型受容野を形成するときに使用します。光が当たると視細胞の膜電位が過分極状態になりますが、双極細胞の中心部付近の入力(直接経路)と周辺部からの入力(関節経路)のうち一方を反転(符号変換)し、拮抗関係にするのです。ON中心型であれば直接経路で、OFF中心型であれば関節経路で符号変換が行われます。
側方抑制
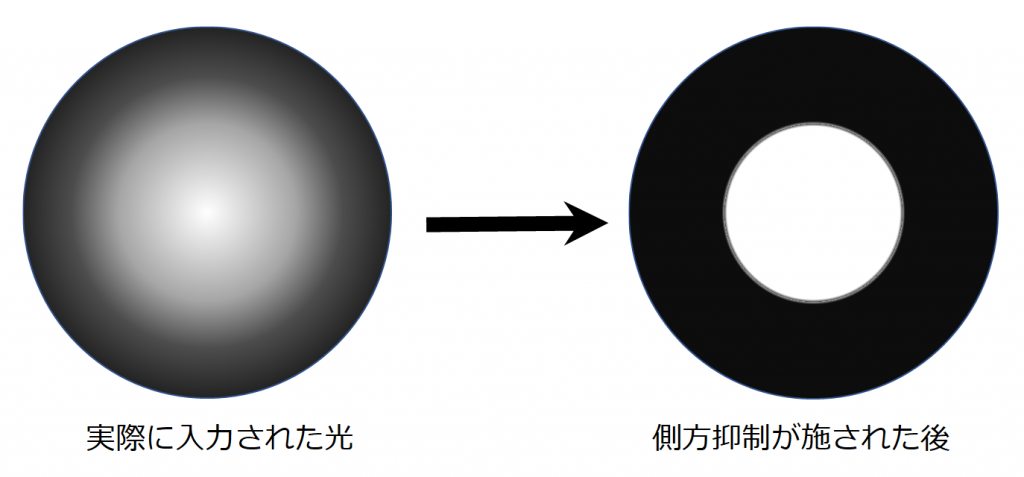
側方抑制は、ある細胞が反応したときに、その周囲に存在する細胞が反応しにくくなるように抑制することです。例として桿体細胞を入力とするON中心型受容野の双極細胞を考えてみます。この受容野に左図のような中心付近がボヤ~と明るい光を当てます。このとき、中心付近の視細胞が最も反応し、周辺の視細胞へ側方抑制がされます。周囲から中心付近への側方抑制も行われますが、明るい方から周囲への側方抑制が強いため、結果的に右図のように中心付近のみが明らかに明かるく映ります。つまり、側方抑制にはコントラストを強くする働きがあるのです。この側方抑制の過程で、周辺の受容野をカバーする水平細胞とアマクリン細胞が関与していると考えられます。
神経節細胞によるAD変換
双極細胞からのアナログ電気信号を一次視覚野まで伝えるには、距離が長いためデジタルに変換する必要があります。この働きをするのが、神経節細胞です。
網膜の情報処理を一文で表すと
網膜の情報処理を一文でまとめると、「カラー画像を、光の明暗(白黒)画像、赤緑画像、青黄画像に分け、補色を利用した中心周辺拮抗型受容野+側方抑制を駆使することでコントラストを強調させている」といえます。
網膜から視覚野へ
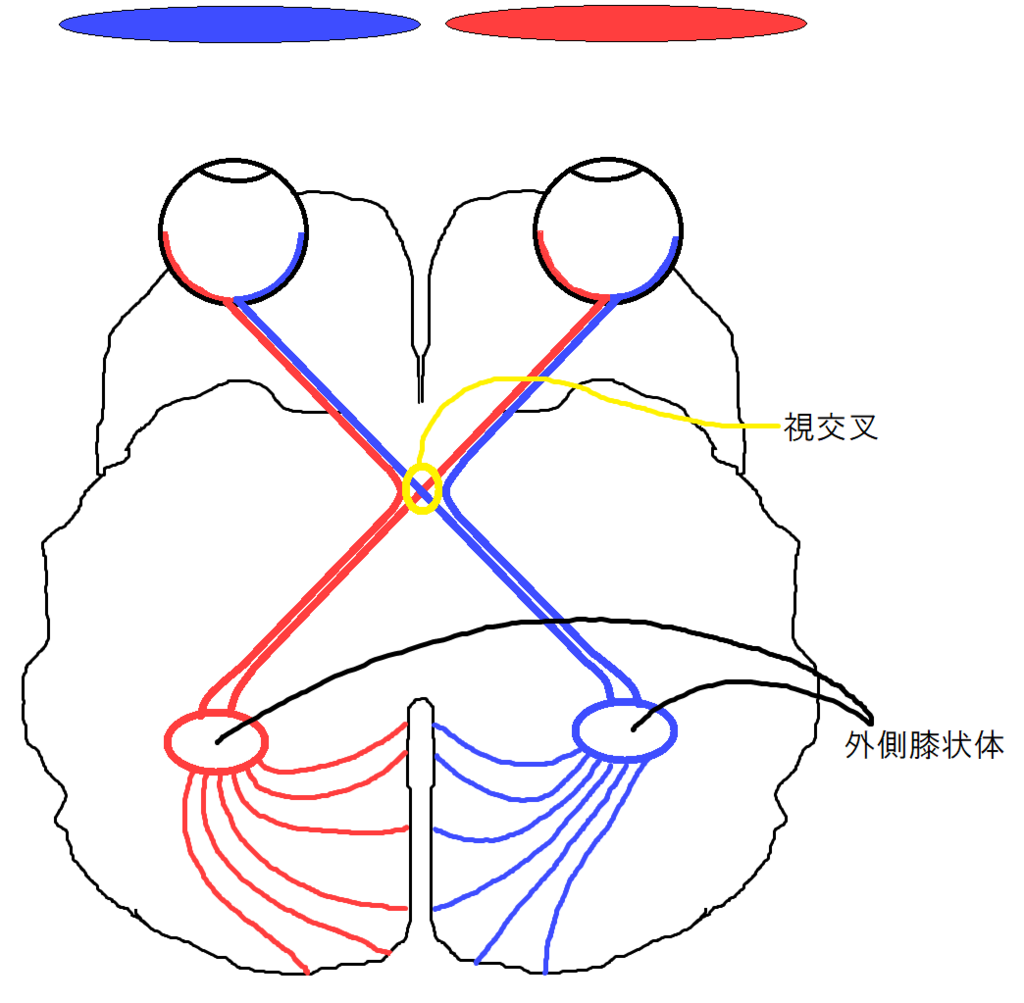
視交叉
左右の眼に入ってきた像はそのまま、脳へ伝わるわけではありません。視交叉((立体視に関与していると考えられている))という部位で、左側風景と右側風景に分離されます。
外側膝状体
外側膝状体では視交叉からの情報を中継し、一次視覚野の対応する部位へ投射します。詳しいことは分かりませんが、一次視覚野からのフィードバックも受けているようです。
視覚野
視覚野では視覚情報処理を行っています。視覚野は図8の色が塗られている部分で、後頭葉から頭頂葉にかけて位置しています。
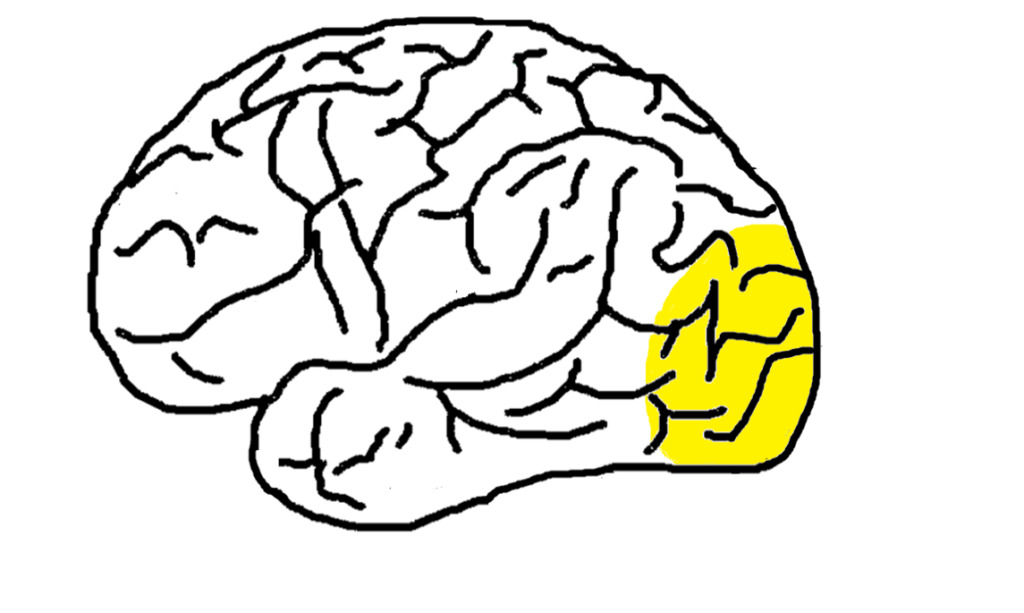
視覚野は一次視覚野(V1)、二次視覚野(V2)、V3、V4、V5に分かれています。以降で説明する単純型細胞と複雑型細胞は一次視覚野に位置しています。
視覚野の情報処理
感覚系では中心周辺拮抗型の受容野を持ちましたが、視覚野からは、より複雑になります。視覚野では、特定の位置にある特定の傾きの線分を認識する単純型細胞(Simple Cell)、特定の傾きの線分が移動しても認識する複雑型細胞(Complex Cell)があります((超複雑型細胞も存在する。))。この細胞はヒューベルとウィーゼルの実験で発見され、興奮領域と抑制領域が明瞭なのが単純型細胞、明瞭ではないものが複雑型細胞と定義されました。
単純型細胞
単純型細胞は図9に示すように、中心周辺拮抗型受容野をもつ外側膝状体の神経細胞が直線状に並んで、一次視覚野の単純型細胞へ入力されます。受容野は楕円形で、少しずつ異なる角度の線に反応する単純型細胞が個々に存在します。
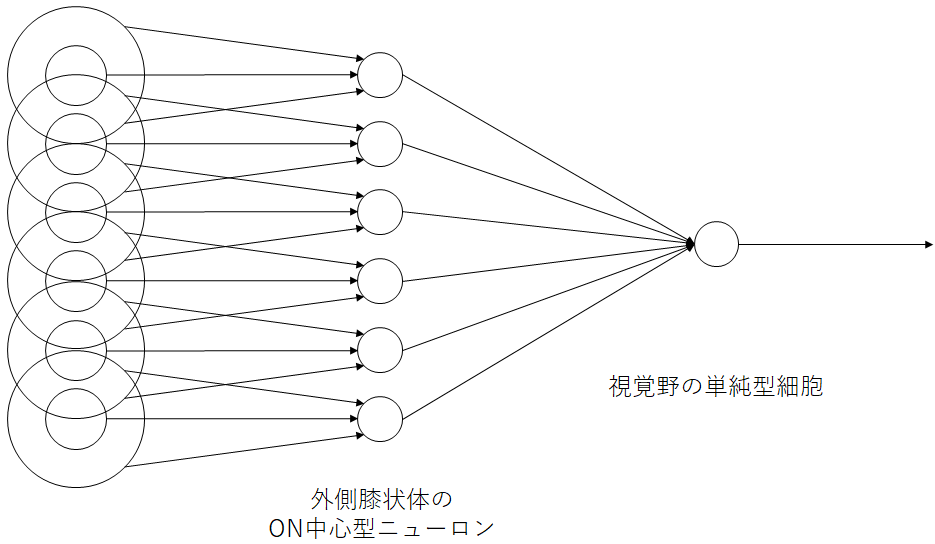
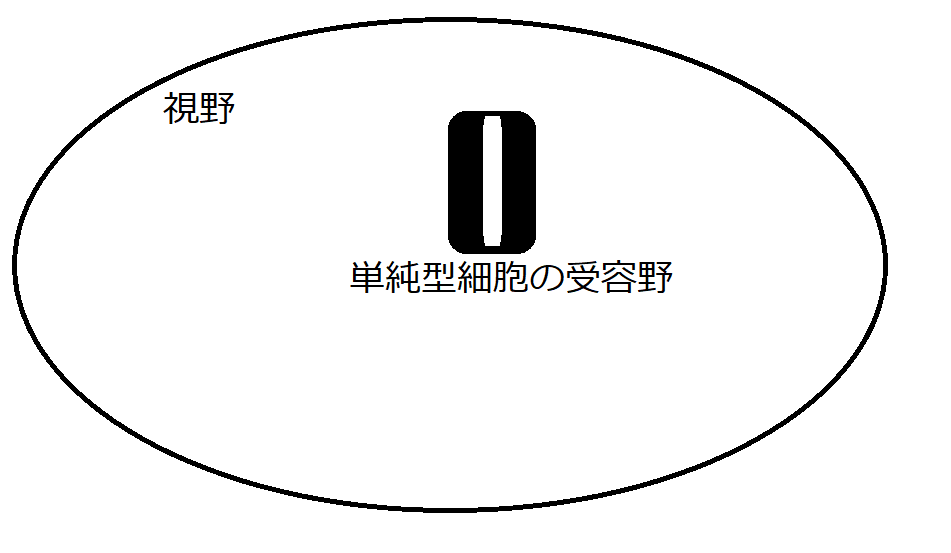
図10は、視野の内部において、図9で示す縦線を認識する単純型細胞が反応を示す領域のイメージです。
複雑型細胞
単純型細胞は特定の位置に映る特定の傾きの線に対してのみ反応しますが、高次の知能を実現するには線の位置が多少動いても、線は線として同様に認識する必要があります。このような位置ずれを許容する細胞が複雑型細胞です。これは、同じ線の特徴に反応を示す単純型細胞を複数入力とする受容野を持つことで、位置ずれを許容できる複雑型細胞を構成できます。図11は、 縦線を認識する単純型細胞が8つ並んだものを入力として受ける複雑型細胞の例です。
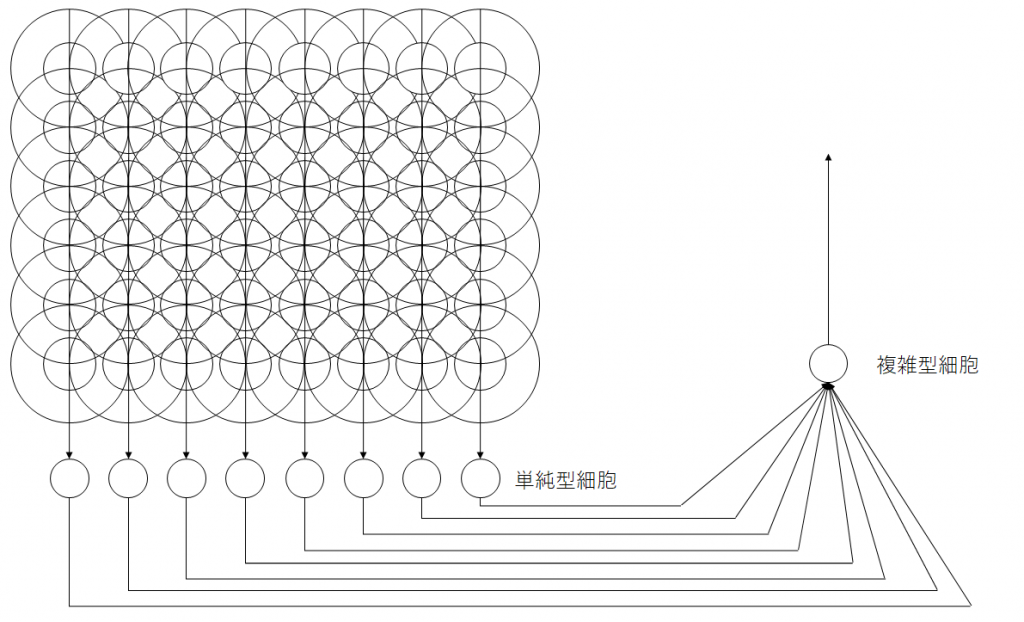
図12は、視野の内部で複雑型細胞がどのような範囲をカバーするかをイメージしたものです。
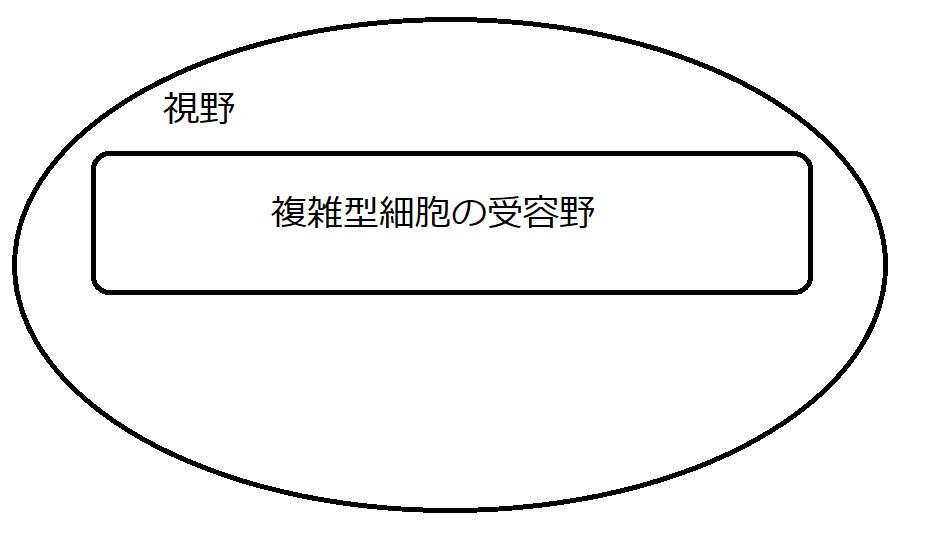
ここから予測できる構造
単純型細胞と複雑型細胞で、階層的に処理が行われていることから、上位層へ進むにつれて、ミクロからマクロへの階層的な処理が続く構造を予測することができます。
ネオコグニトロン
ここまでの内容をモデル化していきます。まず、モデル化のポイントを以下に3点示しました。
- 網膜では画像を受けとり、コントラストの抽出を行う。
- 一次視覚野の単純型細胞(S細胞)は、エッジなどの特徴を抽出する。
- 一次視覚野の複雑型細胞(C細胞)は、位置ずれの許容をする。
1は網膜で行われるため、階層的な繰返しはおこりません。一方で、2と3は大脳皮質で行われており、階層的に繰り返されます。これをモデル化すると以下の図のようになります。
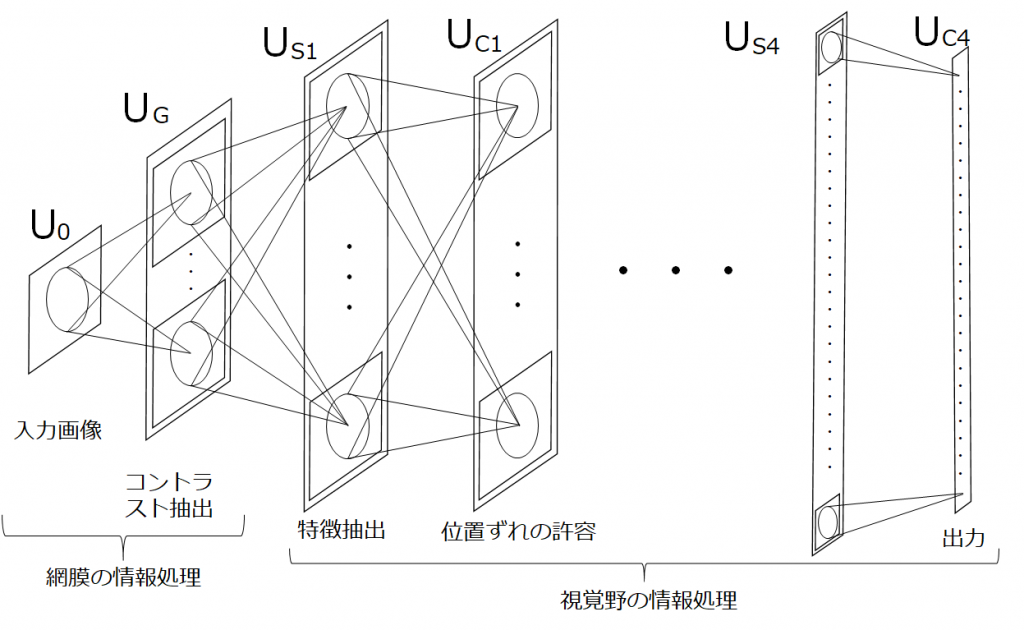
これがネオコグニトロンです。余談ですが、ネオコグニトロンのS細胞層は、畳み込みニューラルネットワークの畳み込み層に、C細胞層は、プーリング層に対応します。
かなりCNNの形に近づいてきましたね。LeNetにもつながりますが、じつはネオコグニトロンは自己組織化を使用した学習を行うため、視覚野における自己組織化について学ぶ必要があります。
今回は、視覚野の方位選択性コラムが自己組織的に、つまり教師な学習により生成される過程を再現してみたいと思います。
視覚野の自己組織化
視覚野における自己組織化
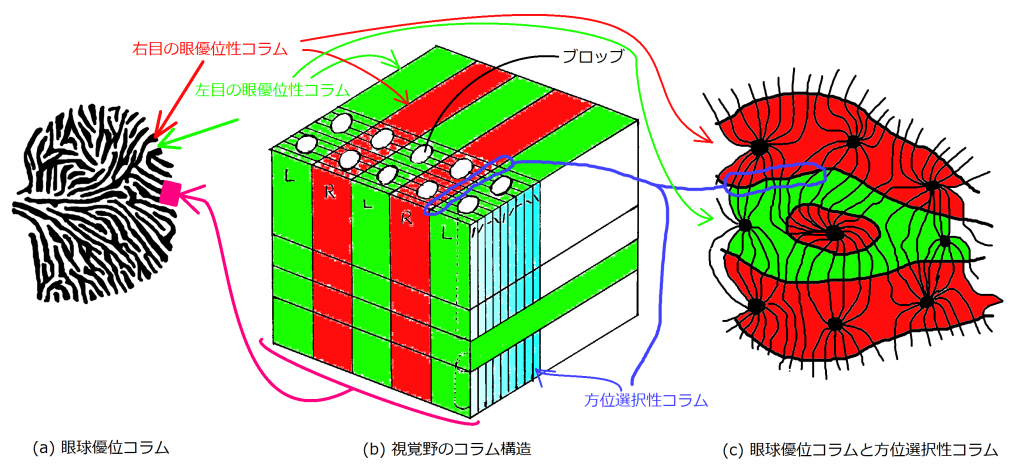
まず、図1の(a)、(b)、(c)について詳しく説明します。
(a)図は視覚野の眼優位性コラムをイメージしたものです。黒色で塗られた部分が右目から情報を受ける眼優位性コラムで、白抜きの部分が左目から情報を受ける眼優位性コラムを表しています。外部の像は網膜で受け取り、視交叉で左右の目からの情報が交差し、外側膝状体を中継して視覚野へ投射されています。
(b)図は(a)図の一部分を縦に切り抜き詳しく表したものです。大脳新皮質は6つの層からできています(図(b)では6層示せていませんが)。図(b)において、右斜め上方向への流れを持つのが眼優位性コラムで、それに垂直に交わる形で方向選択性コラムが並んでいます。方位選択性コラムは特定の傾きにたいして選択的に反応します。少しずつ異なる傾きに反応する方位選択性コラムが並んでいます。
(c)図は、(a)図の一部を拡大したもので、眼優位性コラムの境界面で方位選択性コラムが垂直に交わっていることを示したものです。(b)図は、あくまでモデルであり、方位選択性コラムの並行状態がどこまででも続いていることを仮定しています。実際に、個々の方位選択性コラムが並行な状態は眼優位性コラムの境界面付近であり、境界面以外では一部に集まったり広がったりと、必ずしも並行な状態が続くわけではないことを示しています。(c)は自己組織化の話題で関連性が薄いため、忘れてもらって大丈夫です。
図1では、色分けに一貫性を持たせたので、参考にしてください。
ここで重要な点は、この方位選択性コラムが、教師なしに勝手に(自己組織的に)似た角度のコラムが隣り合う( (c)ではこれを否定しているが...)ように学習が行われることです。これを自己組織化といいます。
自己組織化マップは視覚野のコラム構造が自己組織化されることをモデル化したものです。
感覚系で全体的にいえること
自己組織化は、視覚野だけでなく視覚野でも行われていることが有名で、視覚野や聴覚野に限らず、その他多くの感覚系でも行われています。これは、トポグラフィックマッピングと関連性が強く、自己組織化が関与していると考えられています。この仕組みを実現しようとするアプローチの一つが自己組織化マップといえます。
ちなみに、この話題になると「特定の働きをするニューロンの配置が遺伝子に埋め込まれているにちがいなく、それを使用して再現しているだけだ」と思う方が多いと思いますので、以下に面白い実験結果を紹介します。
聴覚野になるべきところに視覚野が!?
2000年にNature誌に公開された論文で、生まれたばかりで脳が完全に発達していないフェレットを使用して、視覚情報を聴覚野の領域に繋ぎ変えたというものがあります。結果、聴覚野になるはずの領域に、視覚野の方位選択性コラムと方向マップが構築されていました。
気になる方は「Induction of visual orientation modules in auditory cortex.」と検索してみてください。
ここから、 特定の働きをするニューロンの配置は遺伝子により決められているわけではないといえます。
まとめると
ここまでをまとめてみます。
- 大脳において、自己組織化される前は、特定の領野に特定の情報が入力されなければならないという決まりはなく、入力された情報に従って、それぞれの領野を自己組織化すると仮定できる。
- 大脳全領域において一貫した学習手法に従って学習が行われていると仮定できる。(聴覚野の位置で視覚野の学習ができたことから)
特に2が重要です。現在では画像認識や音声認識など認識対象ごとに人間が特徴量やネットワークの型を決めますが、自己組織化なる万能な学習手段が見つかれば、 入力データの性質によらずに特徴抽出から認識まで、同一のネットワークで学習できることを示唆しているのです。
自己組織化マップ
自己組織化マップ(Self-Organizing maps : SOM)はコホネンにより提案されたことにちなみ、コホネンマップやコホネンネットワークともいわれ、入力層と出力層の2層から成り立ちます。出力層は他に競合層ともいわれます。競合層といえば競合学習が思い出されますよね。
以下には、出力層が2次元の例を示します。
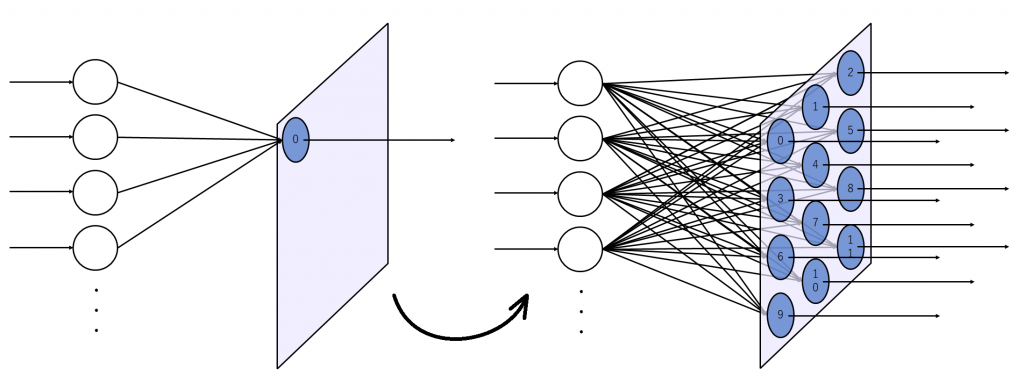
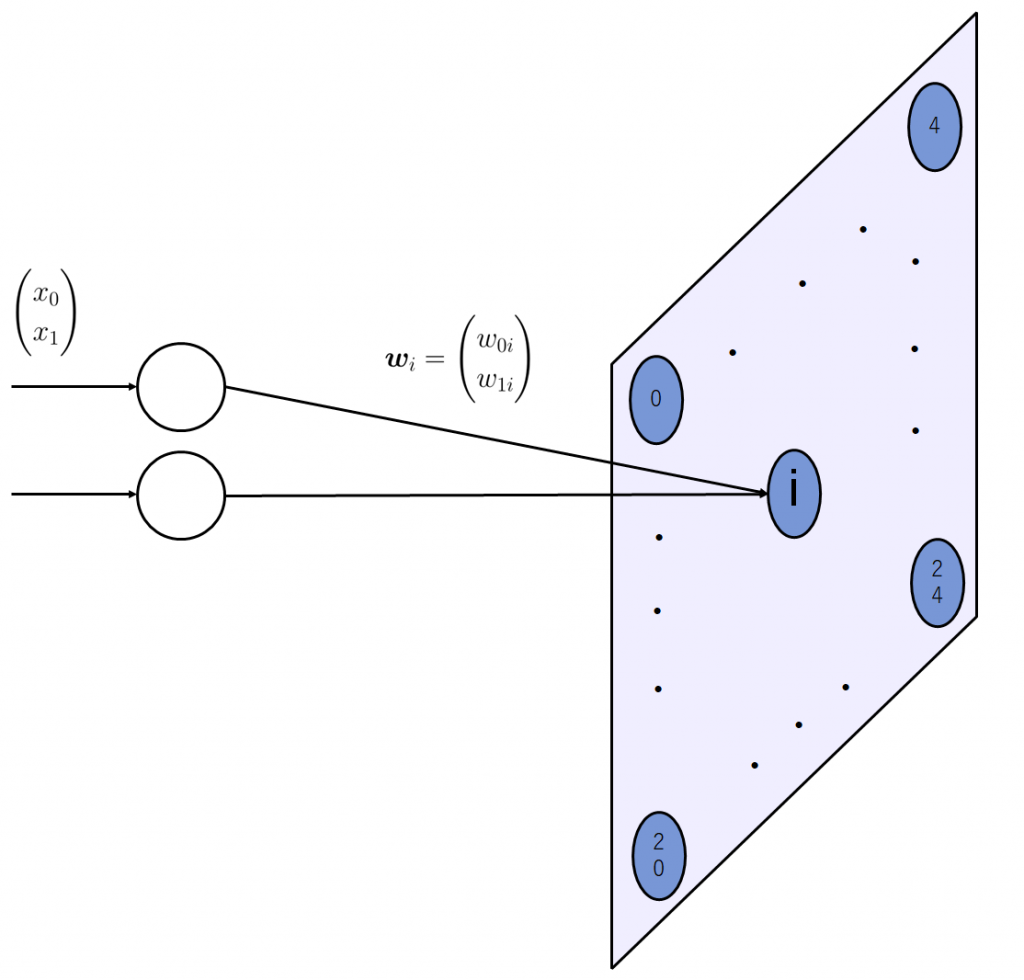
図2(a)は出力層のニューロンが2次元上に配置された状態を示しています。図2(b)は入力層のニューロンを1つ追加した状態を示しています。入力層のニューロンは出力層に存在する全てのニューロンに結合しています。

入力層のニューロン数を増やしてみます。増やした状態が図3です。
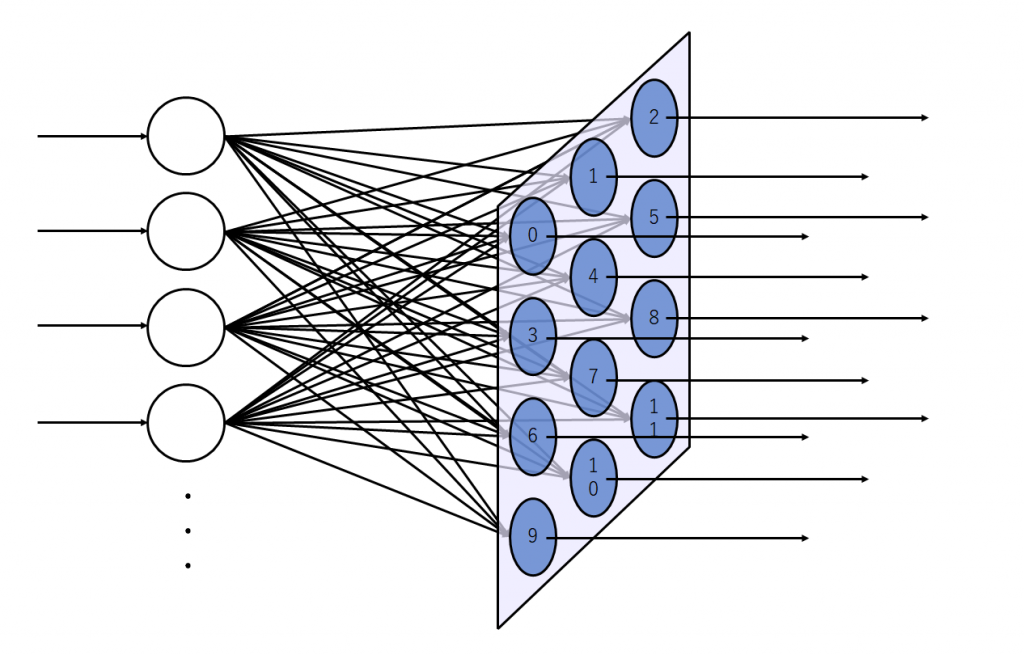
逆の見方もできて、単純パーセプトロンというと語弊がありますが、イメージとしては単純パーセプトロンが並列に沢山並んでいるようなものです。
単純パーセプトロンを含め、ニューロンは入力次元数と等しい数の成分を重みベクトルに持ちます。ニューロンは、線形分離可能な分類問題で、正しく分類できることを目標に習を行います。一方で自己組織化マップは入力ベクトルと重みベクトルが近くなるように学習が行われます。
他のニューラルネットワークと異なるのは、個々のニューロンが個別に学習されるのではなく、マップ上で入力ベクトルに最も近い重みベクトルを持つ勝者ニューロンを中心に学習が行われることです。勝者ニューロンになれなかったニューロンは、勝者ニューロンに倣えという感じに学習がされます。これは、朱に交われば赤くなるというのが最も分かりやすいでしょう。運よく入力ベクトルと近い重みベクトルを持つ勝者ニューロンが影響力をもち、周囲のニューロンに影響をあたえます。つまり、入力データ数がm個のとき、n個の出力層ニューロンの内、m個のみ勝者ニューロンになることが許され、入力データに限りなく近い重みをもてます。周囲のニューロンは学習データとして入力されなかったそれ以外のデータに対応できるように、勝者ニューロンとは少しだけことなる特徴をもちます。自己組織化マップではこのようにして教師なしの自己組織化を実現します。
自己組織化マップの特徴
以下の特徴を頭の片隅に置きつつ、以降の説明を読んでいただければと思います。
・1つの入力に対して発火するニューロンはただ1つ
・教師なし学習である
・大脳における初期の学習を再現している。
・マップ上のニューロンの出力値は内積で決められることが、他のニューラルネットワークのニューロンと同じだが、閾値がニューロンの入力に含まれないことが異なる。
※考え方によってはマップ上のニューロンに閾値が無いわけではない。マップ内のニューロン全ては共通の閾値、つまり、2番目に大きかったニューロンの出力値を閾値として持つと解釈できる。二番目に大きいニューロンの出力値をマップ上の全てのニューロンから引き、正か負かを単位ステップ関数で量子化し、その行列を実際のマップの出力値とアダマール積する。これにより勝者ニューロン以外は0、勝者ニューロンはその出力値を出力できる。
出力層の出力
自己組織化マップの出力層において、発火するニューロンは入力データ1つにつき1つだけです。入力ベクトルに最も近い重みベクトルを持つ、つまり、マップ(出力層)上のニューロンの中で内積の値が最も大きかったもの以外は、0に丸められます。これを数式に表すと、以下のようになります。
入力ベクトルを\(\boldsymbol{x} = (x_0\ x_1\ \cdots\ x_m)^T\)
マップ上\(i\)番目のニューロンの重みベクトルを \(\boldsymbol{w_i} = (w_{0i}\ w_{1i}\ \cdots\ w_{mi})^T\)
全てのニューロンの重みを横に並べ行列にしたものを\(\boldsymbol{W}\)
\( y_i =
\begin{cases}
\boldsymbol{w_i}^T\boldsymbol{x} & (i == argmax (\boldsymbol{W}^T\boldsymbol{x}) )\\
0 & (i != argmax (\boldsymbol{W}^T\boldsymbol{x}) )
\end{cases}
\)
これは、argmaxで出力が最大となったニューロンのインデックスを取得し、それが\(i\)であれば、その値を、\(i\)でなければ0を出力することを表しています。
重みの更新方法
自己組織化マップの入力層および出力層の次元数に制限はありません。、また、入力次元数が\(m\)、出力次元数が\(n\)ならば、出力層の各ニューロンは\(m\)個の成分を持つベクトルになります。それぞれのニューロンの持つ重みベクトルが、入力ベクトルにどの程度似ているかを出力層のニューロン同士で競争させます。勝ち抜いたニューロン、つまり最も入力ベクトルに近い重みベクトルを持っていたニューロンの重みが、更に入力ベクトルに近づくように調節し、周囲も勝者ニューロンからの距離に応じた影響をうけ、重みが入力ベクトルに近づけられます。
\(i\)番目のニューロンの重み更新の手順を以下に示します。
①勝者ニューロンから\(i\)番目のニューロンまでの距離を求める。
➁①で求めた距離を正規分布に代入し、係数\(h_i\)を取得する。
➂学習率\(c\)を定め、\(\boldsymbol{w}_i^{(t+1)} = \boldsymbol{w_i}^{(t)} + ch_i(\boldsymbol{x} - \boldsymbol{w_i}^{(t)})\)
で重みを更新する。
※実際の学習ではブロードキャストルールを使用して、一気に全てのニューロンの重みを更新します。この場合、勝者ニューロンからどのくらい影響を受けるかを調節する係数\(h_i\)を、並べたベクトルを\(H\)として、
\(\boldsymbol{W}^{(t+1)} = \boldsymbol{W}^{(t)} + cH(\boldsymbol{x} - \boldsymbol{W}^{(t)})\)
で重み更新を行います。
Pythonによるプログラム例
使用する入力データ
今回自己組織化マップで教師なし学習をさせるのは、二次元の4つのベクトル
\(
\begin{pmatrix}
1\\0
\end{pmatrix},
\begin{pmatrix}
0\\1
\end{pmatrix},
\begin{pmatrix}
-1\\0
\end{pmatrix},
\begin{pmatrix}
0\\-1
\end{pmatrix} \)
です。用意するのは、これだけです。教師信号はありません。これを入力するだけで、出力層のマップには、それ以外の二次元入力
\(
\begin{pmatrix}
\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}
\end{pmatrix}
\)
などに反応するニューロンが"自己組織的"に生成されます。
今回学習に使用する自己組織化マップの形状
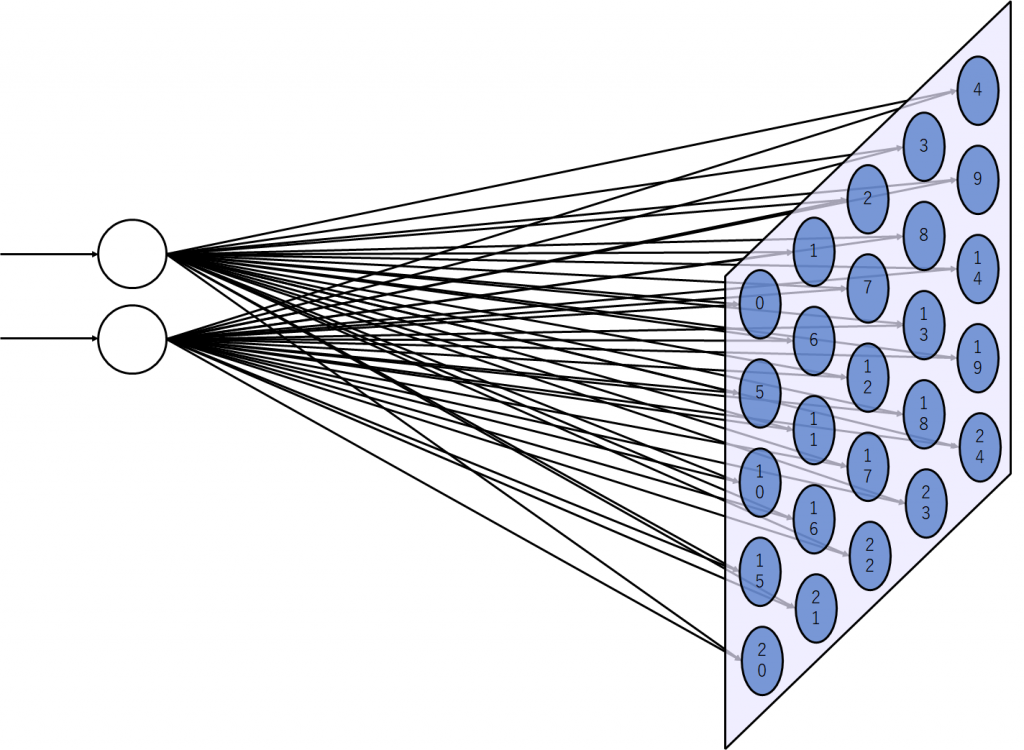
入力データは二次元ベクトルなので、入力層のノード数は2つです。マップは5×5に設定しました。これにより、学習後は入力される全ての二次元ベクトルパターンは25個の特徴に分けられることになります。
Pythonでプログラムを書いてみる
最初に必要なライブラリ及び関数をインポートします。
import numpy as np
import matplotlib.pyplot as plt
#ガウス分布の確率密度関数をインポート
from scipy.stats import normつぎに、入力データを定義します。
X = np.array([[1, 0, -1, 0],
[0, 1, 0, -1]])自己組織化では、出力層の全てのニューロンが自分の位置を把握((私の憶測ですが、実際の脳ではグリア細胞が学習に関与することで、このような位置関係を考慮した学習が可能になっていると考えます。))していなければならないので、図5のようにマップの座標を定めます。
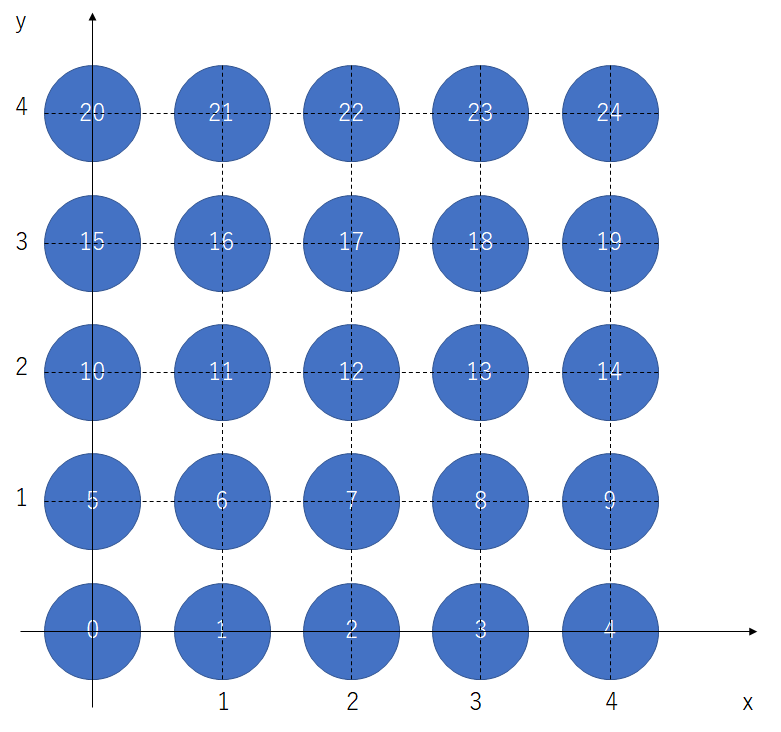
位置を列ベクトルで表し、それを25個並べて、行列にします。
Vec = np.array([[0,1,2,3,4,0,1,2,3,4,0,1,2,3,4,0,1,2,3,4,0,1,2,3,4],
[0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4]])次に個々のニューロンの重みを正規分布に従ってランダムに生成します。以下の重み行列は、列ベクトルを25個並べたものです。
W = np.random.rand(2, 25)自己組織化マップでは入力ベクトルと重みベクトルがどれだけ似ているかを、競争して学習するため内積を使用しますが、それぞれの重みベクトルの大きさが異なると、互いに正しい比較ができないため、それぞれが単位ベクトルになるように正規化します。
W = W / np.linalg.norm(W, axis=0)この初期状態で、マップ上のニューロンがどの向きのベクトルを持っているのか、プロットしてみます。
plt.figure()
plt.quiver(Vec[0, :], Vec[1, :], W[0, :], W[1, :], angles='xy', scale_units='xy', scale=1)
plt.xlim([-1,5])
plt.ylim([-1,5])
plt.grid()
plt.axes().set_aspect('equal')
plt.show()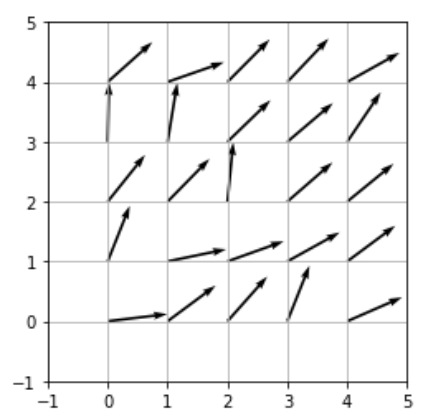
初期状態なので、それぞれのニューロンが持つ重みベクトルの向きはバラバラです。それでは、まず一つずつ学習手順を追っていきます。
1.学習データを一つ選びます。ここではX[:, 0]を選びました。そして、入力ベクトルX[:, 0]と重みベクトルの近さ、つまり、内積を計算します。
そして、出力結果が最大のニューロンのインデックスをjに代入します。
j = np.argmax(np.dot(W.T, X[:, 0]))2.j番目のニューロン(勝者ニューロン)からみた他のニューロンの位置ベクトルを計算しユークリッド距離に変換します。
D_Vec = Vec - Vec[:, j][:, np.newaxis]
D = np.linalg.norm(D_Vec, axis=0)3.勝者ニューロンから近いところほど影響を受け、遠いニューロンほど影響を受けにくくするために、ガウス関数を使用して、距離に応じた係数を決定します。
H = norm.pdf(D)4.重みベクトルを更新し、単位ベクトルに変換します。
W = W + c * H * (X[:, 0][:, np.newaxis] - W)
W = W / np.linalg.norm(W, axis=0)ここまでが、1回分の学習です。これを4つの学習データを順番に変更しながら、10000回反復させるようにプログラムしたものが、以下になります。
#学習率cを0.01にセット
c = 0.01
#4つの入力データを10000回学習させる
for _ in range(10000):
#iは4つの学習データから1つを選ぶ
for i in range(4):
#内積(入力ベクトルと重みベクトルの向きの近さ)を計算した結果、
#最も値の大きかったニューロン(勝者ニューロン)のインデックスを取得する
j = np.argmax(np.dot(W.T, X[:, i]),axis=0)
#勝者ニューロンから見た時の周囲のニューロンの位置ベクトルを計算する
D_Vec = Vec - Vec[:, j][:, np.newaxis]
#D_Vecの列方向において、ユークリッド距離を計算する
D = np.linalg.norm(D_Vec, axis=0)
#勝者ニューロンを中心にガウス分布に従う割合で、入力データに
#重みベクトルを近づけるための係数ベクトルHを取得する
H = norm.pdf(D, scale=2)
#全てのニューロンの重みベクトルを更新する
W = W + c * H * (X[:, i][:, np.newaxis] - W)
#それぞれの重みベクトルを単位ベクトルに正規化する
W = W / np.linalg.norm(W, axis=0)どのように重みベクトルが変化したか可視化してみましょう。
重み行列を初期化するときに、どの様なランダム値が生起したかにより、自己組織化マップの結果が変わるので、4パターンを実験してみました。
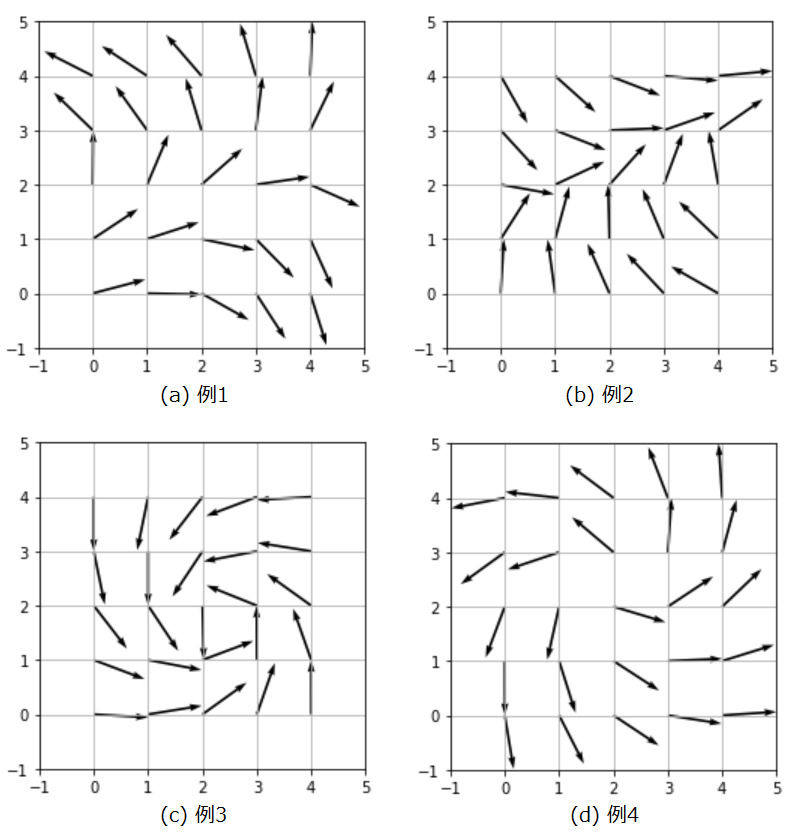
自己組織化マップにより視覚野の方位選択性コラムが、近い傾きが隣り合うように配置されるという現象を簡単な例を用いてシミュレーションできました。
プログラムをすべて示します
import matplotlib.pyplot as plt
#ガウス分布の確率密度関数をインポート
from scipy.stats import norm
X = np.array([[1, 0, -1, 0],
[0, 1, 0, -1]])
Vec = np.array([[0,1,2,3,4,0,1,2,3,4,0,1,2,3,4,0,1,2,3,4,0,1,2,3,4],
[0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4]])
W = np.random.rand(2, 25)
W = W / np.linalg.norm(W, axis=0)
#学習率cを0.01にセット
c = 0.01
#4つの入力データを10000回学習させる
for _ in range(10000):
#iは4つの学習データから1つを選ぶ
for i in range(4):
#内積(入力ベクトルと重みベクトルの向きの近さ)を計算した結果、
#最も値の大きかったニューロン(勝者ニューロン)のインデックスを取得する
j = np.argmax(np.dot(W.T, X[:, i]),axis=0)
#勝者ニューロンから見た時の周囲のニューロンの位置ベクトルを計算する
D_Vec = Vec - Vec[:, j][:, np.newaxis]
#D_Vecの列方向において、ユークリッド距離を計算する
D = np.linalg.norm(D_Vec, axis=0)
#勝者ニューロンを中心にガウス分布に従う割合で、入力データに
#重みベクトルを近づけるための係数ベクトルHを取得する
H = norm.pdf(D, scale=2)
#全てのニューロンの重みベクトルを更新する
W = W + c * H * (X[:, i][:, np.newaxis] - W)
#それぞれの重みベクトルを単位ベクトルに正規化する
W = W / np.linalg.norm(W, axis=0)
plt.figure()
plt.quiver(Vec[0, :], Vec[1, :], W[0, :], W[1, :], angles='xy', scale_units='xy', scale=1)
plt.xlim([-1,5])
plt.ylim([-1,5])
plt.grid()
plt.axes().set_aspect('equal')
plt.show()ネオコグニトロンから畳み込みニューラルネットワークへ
ネオコグニトロンと畳み込みニューラルネットワーク

ネオコグニトロンはUg層でコントラスト抽出(エッジを検出しやすくするためにエッジ強調を行っている)を行い、Us層で特徴抽出、Uc層で位置ずれの許容をします。視覚野において特徴抽出は単純型細胞、位置ずれの許容は複雑型細胞が行っていることを第1回目に説明しました。Ugは最初のみですが、UsとUcは階層的に繰り返されます。繰り返すにつれて、画像データから配列に近づいていきます。
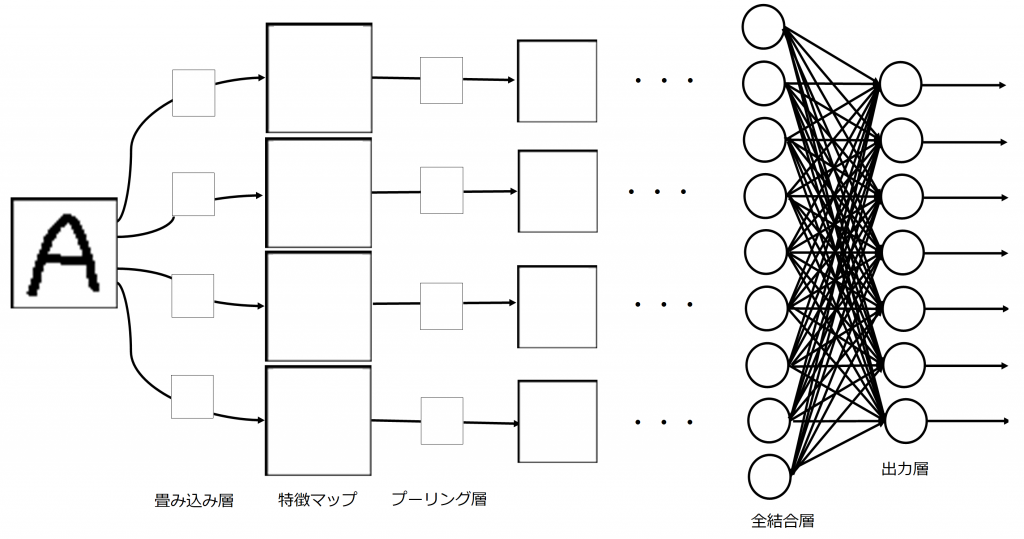
畳み込みニューラルネットワークでは、Ug層、Us層を畳み込み層、Uc層をプーリング層として実現させます。畳み込み層とプーリング層が階層的に繰り返される過程で、分類に必要な特徴量が抽出されていき、最後に全結合層(一般的なニューラルネットワーク)により、所望の出力層ニューロンに反応が対応するよう写像されます。プーリング層では平均プーリングや最大プーリングなどがありますが、最大プーリングが最もよく使用されます。複雑型細胞が任意の反応が受容野内で起こるかぎり反応を示すことを考慮すると、プーリング処理として最も強い特徴量を残す最大プーリングを使用することは理にかなっているといえます。
ネオコグニトロンと畳み込みニューラルネットワークの違い
ネオコグニトロンと畳み込みニューラルネットワークの主な違いは学習方法です。詳しく触れませんが、ネオコグニトロンではAdd-if Silentという学習手法がとられます。一方で、畳み込みニューラルネットワークでは一般的なニューラルネットワークと同様で誤差関数による勾配降下法と誤差逆伝播により畳み込みフィルターの重みと全結合層の重みが学習されます。
LeNet
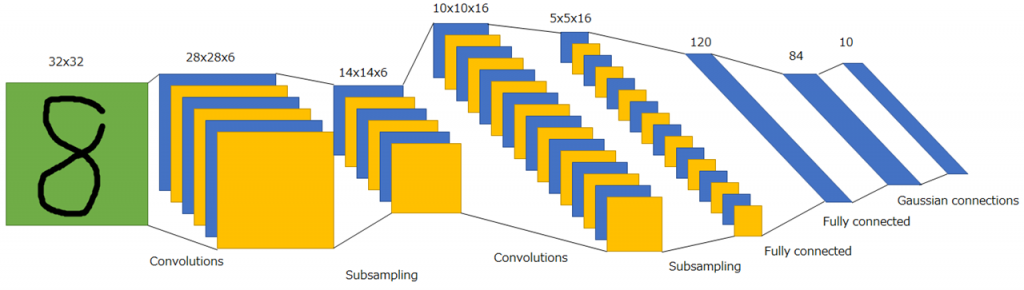
最後に
もっと知りたい方は、以下の記事がお勧めです。内容が多少被るところがあるとは思いますが、こちらでは、PyTorchを使用して、LeNetを実装しています。