この記事では、移動ロボットのナビゲーションに広く採用されているDynamic Window Approach(DWA)について、わかりやすくご紹介します。DWAは、そのシンプルな仕組みにも関わらず、自然な障害物回避を実現します。この記事の後半ではDWAを強化学習と組み合わせた研究事例にも触れます。これにより、例えば人間のような移動障害物を避けることが可能になります。完璧なソリューションではないにせよ、現実の応用において非常に興味深いアプローチであるため、この記事を通じてDWAの基本とその可能性について理解を深めていただければと思います。
3つの要点
では、まず最初に、DWAの3つの要点を記載します。これだけはまず覚えておいてください。
- DWAは移動ロボットの実現可能な速度と角速度、物理的制約を考慮して経路を複数計画
- 生成した複数の経路から評価関数を用いて最適な経路を選択
- 強化学習と融合することで移動障害物回避への応用も可能
パスプランニングの概要
DWA[1]は、ロボットのパスプランニングの中で重要な役割を果たすローカルパスプランニング技術ですが、そもそも、パスプランニングとは何を意味するのでしょうか?
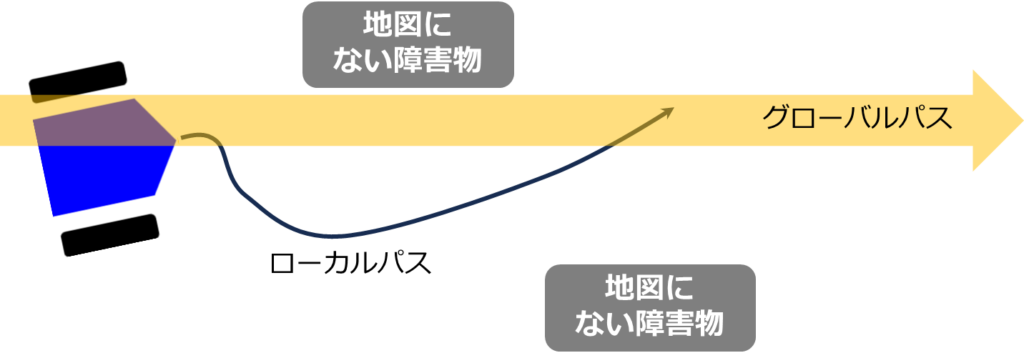
簡単に言うと、パスプランニングは移動ロボットが現在位置から目標位置までの最適な経路を決定するプロセスです。このプロセスは、私たちが目的地に向かう際に地図を用いて経路を計画する行為に似ています。初期の計画段階では、信号の状態や歩行者の動きなどの細かい要素を考慮せずに、大まかに最短距離や最短時間で目的地に到達する経路を選択します。実際に移動を開始すると、信号や歩行者に応じてリアルタイムで経路を調整する必要があります。この初期段階の計画をグローバルパスプランニング、リアルタイムの調整をローカルパスプランニングと呼びます。
ロボットの経路計画においても同様のアプローチが採用されています。グローバルパスプランニングでは、A*やダイクストラのようなアルゴリズムを使用して、地図上での最適な経路を計画します。この計画された経路は、道路工事などの予期せぬ障害がない限り、頻繁には変更されません。一方、ローカルパスプランニングでは、グローバルパスプランニングで計画された経路に基づきながら、リアルタイムで環境の変化に対応して経路を調整します。これには、地図に記載されていない静止または移動する障害物への対応が含まれます。DWAなどのアルゴリズムがここで活躍し、グローバルパスプランナーによって提供された経路を局所的に最適化して、よりスムーズで効率的な移動を実現します。
Dynamic Window Approach(DWA)の概要
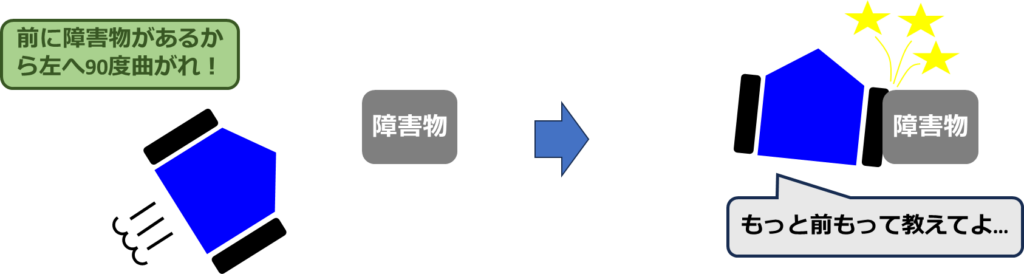
多くの既存のローカルパスプランニング手法では、ロボットの物理的な制約の順守が不十分な場合が多いです。これは、ロボットが実際に達成できる速度、角速度、加速度といった物理的な制約が考慮されていないことを意味します。その結果、制御命令がロボットの実行可能な動作範囲を超え、ロボットはこれらの命令に従うことができず、予期しない動作を引き起こす可能性があります。
さらに、強化学習を用いたローカルパスプランニング手法でも、方策がロボットの実際の動作範囲を正確に反映していないことが問題となることがあります。これは、方策がロボットの物理的な限界を完全には捉えられないことに起因し、実世界での適用時に予期しない結果を招く原因となり得ます。
※強化学習モデルのみを用いたローカルパスプランニングでは、左右に振動するような小刻みな動作がみられます。
したがって、ロボットの物理的な制約を正確に考慮し、実行可能な動作範囲内での制御を保証することが、ローカルパスプランニング手法の開発において重要です。
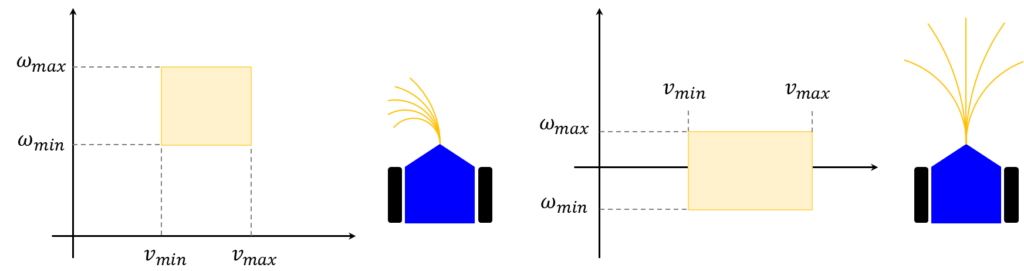
Dynamic Window Approach(DWA)は、探索範囲の動的な調整と最適経路の選択を行うことで、効率と安全性を両立させるパスプランニング手法で、比較的自然な障害物回避動作を実現することができます。このアプローチの核心は、「Dynamic Window」と呼ばれる概念にあります。これは、ロボットの現在の速度と角速度を基に、次の瞬間までに対応可能な速度と角速度の範囲を計算することから名付けられました。このプロセスにより、DWAは、その範囲内で実現される将来の経路の候補を生成します。

DWAでは、ロボットが目標地点に向かって進む際の接近度合い、障害物を避ける能力、および速度を数値的に評価します。この評価は、評価関数\(G(v,\omega)\)を用いて行われます。
$$
G(v, \omega) = \sigma (\alpha\cdot heading(v, \omega)+\beta\cdot dist(v, \omega) + \gamma\cdot velocity(v, \omega))
$$
ここで \(\alpha, \beta, \gamma\)は重み付けパラメーターです。この評価関数の最大値を持つ速度\(v\)と角速度\(\omega\)の組み合わせが選択されます。このプロセスにより、DWAは、ロボットが効率的かつ安全に目標に向かって進むための最適な経路を選択することができます。
DWAの詳細プロセス
ここからは、DWAの詳細プロセスについて説明します。
実行可能な円弧経路の探索範囲の動的な調節
メージとして捉えると、速度 \(v\)と角速度\(\omega\) を軸とする座標系上で、選択可能な速度と角速度の範囲を描くと、窓の形状が現れます。この「窓」は、ロボットの現在の状態と物理的制約に応じて適切に変化します。この特性が、手法の名前である「Dynamic Window Approach(DWA)」の由来となっています。つまり、この動的な「窓」は、ロボットが次の瞬間に取り得る動作の範囲を示しており、その範囲内から最適な速度と角速度が選択されるのです。このアプローチにより、ロボットは環境の変化に柔軟に対応しながら、目標地点に向けて効率的かつ安全に進むことが可能になります。
探索空間の絞り込み
先ほどの概要から、Dynamic Window Approach(DWA)の基本的なイメージを掴んでいただけたと思います。しかし、実際には、このアプローチはより数学的な計算を伴います。具体的には、実行可能な速度と角速度の集合\(V_r\)(下付き文字の\(r\)はresultから)は、以下の三つの集合の交差によって定義されます。
$$
V_r = V_s\cap V_a \cap V_d
$$
ここで、各集合は以下のように定義されます。
| \(V_s\) | 可能な全ての速度と角速度の集合。 これは、ロボットの物理的な能力によって定義される速度と角速度の全範囲。 |
| \(V_a\) | 許容可能な速度・角速度の集合。 これは、ロボットの安全性やその他の制約条件を考慮して選ばれた許容可能な速度と角速度の範囲。 |
| \(V_d\) | Dynamic Windowによる集合。 これは、ロボットの現在の速度と加速度を基に計算され、短期間内にロボットが到達できる速度と角速度の範囲。 |
これらの集合を組み合わせることで、ロボットが現在の状態から安全に操作可能で、かつ物理的に実行可能な速度と角速度の範囲を特定します。DWAはこの範囲内から、目標位置に向かう効率と安全性を最大化する速度と角速度の組み合わせを選択するための計算を行います。
3つの集合が組み合わされるイメージを下図に示します。取りうる\((v,\omega)\)の集合\(V_s\)があって、その一部が障害物にぶつかる可能性がある円弧経路を生成する組み合わせになるため\(V_a\)でフィルタリングし、更に現在の速度や角速度と物理的な制約に基づいて実行可能な組み合わせが\(V_d\)によってフィルタリングされ\(V_r\)(下図の赤色領域)を得ます。
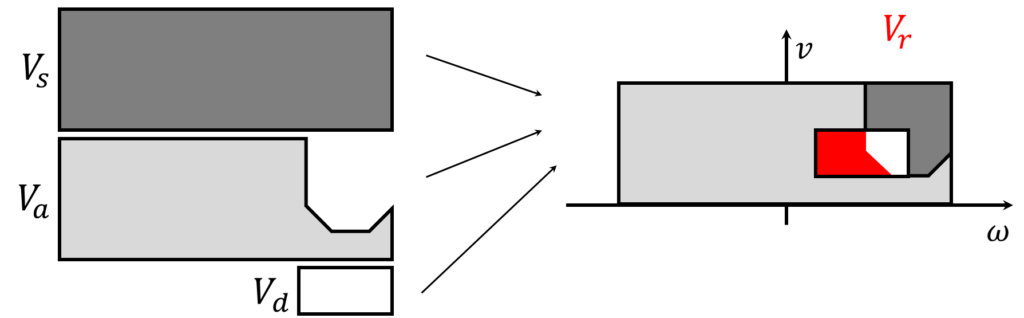
以下では\(V_a\)と\(V_d\)について詳しく説明します。
\(V_a\)の定義
Dynamic Window Approach(DWA)における\(V_a\)の定義について解説します。\(V_a\)は、ロボットがその場で停止できる範囲内の速度と角速度の集合を意味します。この集合は、物理学の基本原則に基づいて計算されます。具体的には、ロボットが最大加速度\(\dot{v}_{max}\) と最大角加速度\(\dot{\omega}_{max}\) を用いて最近傍の障害物に向かって移動した際に、安全に停止可能な速度と角速度の範囲を示しています。この計算は、物理学の等加速度運動の公式 \(v=\sqrt{2gh}\) に似ており、ここでは\(g\)と\(h\)がそれぞれ加速度と移動距離に対応します。
$$
V_a = \left\{(v, \omega) | v \leq \sqrt{2\cdot dist(v,\omega)\cdot\dot{v}_{max}} \wedge \omega \leq \sqrt{2\cdot dist(v,\omega)\cdot\dot{\omega}_{max}}\right\}
$$
ここで、\(dist(v,\omega)\)は、速度\(v\)と角速度\(\omega\)で移動する際の円弧経路と最近傍の障害物との距離を表します。この定義により、ロボットが障害物に衝突することなく、安全に停止可能な速度と角速度の範囲がフィルタリングされます。
\(V_d\)の定義
Dynamic Window Approach(DWA)で使用される集合\(V_d\)は、Dynamic Windowによって定義される速度と角速度の実現可能な範囲を指します。この集合は、ロボットが次の時間ステップで到達可能な速度と角速度の範囲を具体的に示しています。数式で表現すると、以下のようになります。
$$
V_d = \left\{(v, \omega) | v \in [v_{t-1, min}, v_{t+1,max}] \wedge \omega \in [ \omega_{t-1, min}, \omega_{t+1,max}] \right\}
$$
ここで、\(v_{t-1, min}, v_{t+1,max}, \omega_{t-1, min}, \omega_{t+1,max}\)は次のように計算されます(原論文とは少し異なります)。
$$\begin{eqnarray}
v_{t+1, min} &=& \max(v_t-\Delta v, v_{min}) \\
v_{t+1, max} &=& \min(v_t+\Delta v, v_{max}) \\
\omega_{t+1, min} &=& \max(\omega_t-\Delta \omega, \omega_{min}) \\
\omega_{t+1, max} &=& \min(\omega_t+\Delta \omega, \omega_{max}) \\
\end{eqnarray}$$
ここで、\(v_{min}, v_{max}, \omega_{min}, \omega_{max}\) はロボットが出せる速度と角速度の最小値および最大値を示し、\(\Delta v, \Delta \omega\) は1ステップでロボットが対応できる速度と角速度の変化量を指します。この計算により、ロボットの現在の速度と角速度に基づき、次のステップで安全に達成できる速度と角速度の範囲が決定されます。この範囲は、ロボットの物理的な能力と環境条件を考慮した上での最適な選択肢を絞り込むことに役立ちます。
評価関数について
評価関数\(G(v, \omega)\)は、\((v,\omega)\)の良さを数値化するために用いられる関数で、DWAでの最適な動作選択に重要な役割を果たします。再掲すると、この評価関数は以下のように定義されます。
$$
G(v, \omega) = \sigma (\alpha\cdot heading(v, \omega)+\beta\cdot dist(v, \omega) + \gamma\cdot velocity(v, \omega))
$$
ここで、\( heading(v, \omega), dist(v, \omega), velocity(v, \omega)\)はそれぞれ進行方向、障害物までの距離、速度に関する評価項目であり、\(\alpha, \beta, \gamma\)はこれらの項目の重要度を調整するための重みです。
\(heading(v,\omega)\)
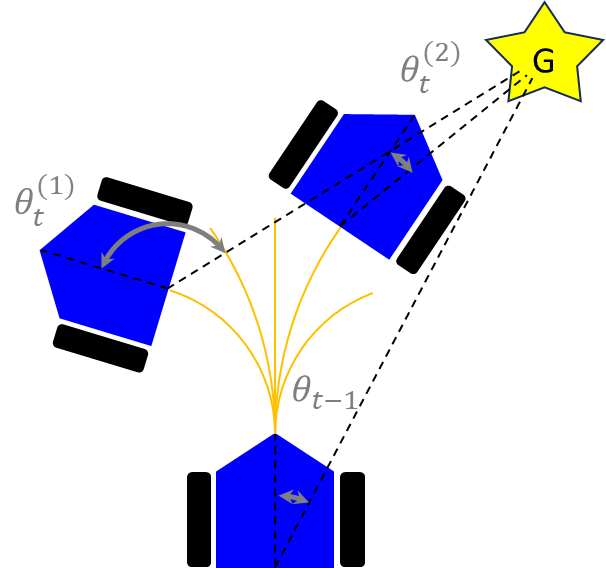
\(heading(v, \omega)\)は、予測経路の終端におけるロボットの進行方向とゴール方向との一致度合いを評価する関数です。具体的には、組み合わせ\((v^{(i)},\omega^{(i)})\)を事前に設定した分だけ実行したときに到達すると考えられる位置(予測円弧経路の終端)でのロボットの進行方向から見たゴール方向との絶対角度差を扱います。この評価は、ロボットがゴールに向かってどれだけ適切に進行しているかを数値化します。
計算式は、予測される各組み合わせ\((v^{(i)},\omega^{(i)})\)に対して次のようになります。
$$
heading(v^{(i)},\omega^{(i)}) = 180-|\theta^{(i)}|
$$
ここで、\(\theta^{(i)}\)は、予測されたロボットの進行方向とゴール方向との角度差です。この式では、180度から角度差の絶対値を引くことで、ゴールに直接向かっている状態を高く評価します。角度差が小さいほど、つまり\(heading(v^{(i)},\omega^{(i)})\)の値が大きいほど、ロボットがゴールに向かっていると判断されます。
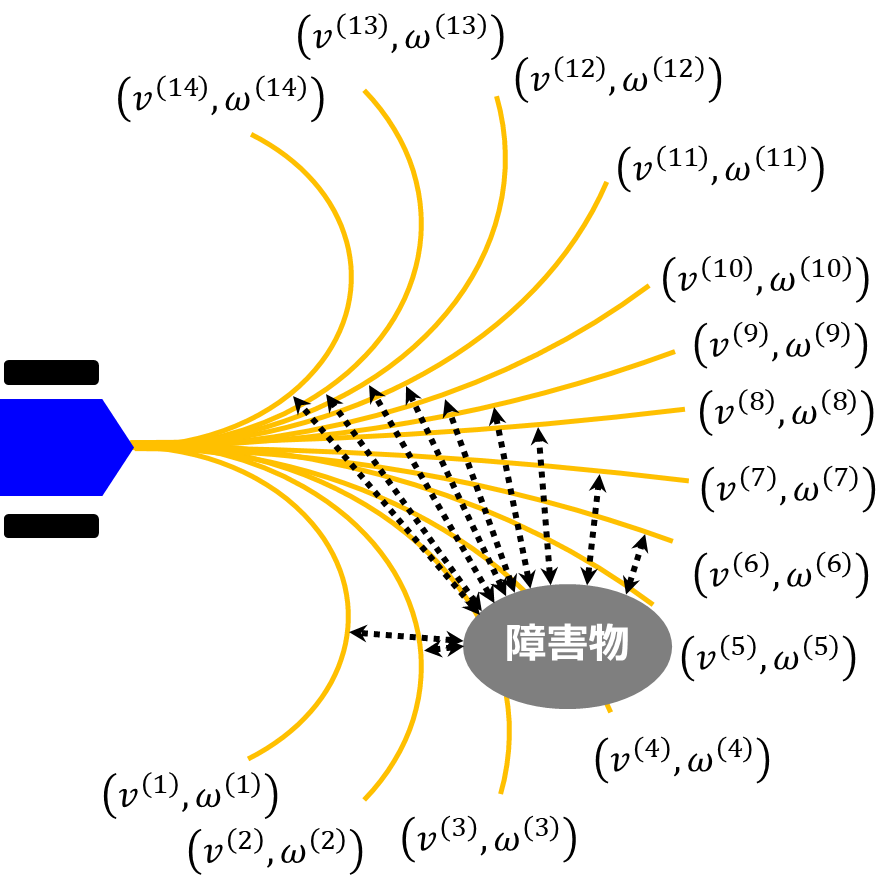
\(dist(v,\omega)\)
\(dist(v,\omega)\)は、ロボットが特定の速度\(v\)と角速度\(\omega\)で移動した場合に最近傍の障害物とどのくらいの距離をとって移動できるかを評価する指標です。下図に示すように、予測円弧経路において近傍の障害物に最接近したときの距離が\((v^{(i)},\omega^{(i)})\)のスコアになります。つまり、障害物に接近する経路よりも、離れている経路のほうが値が高くなります。
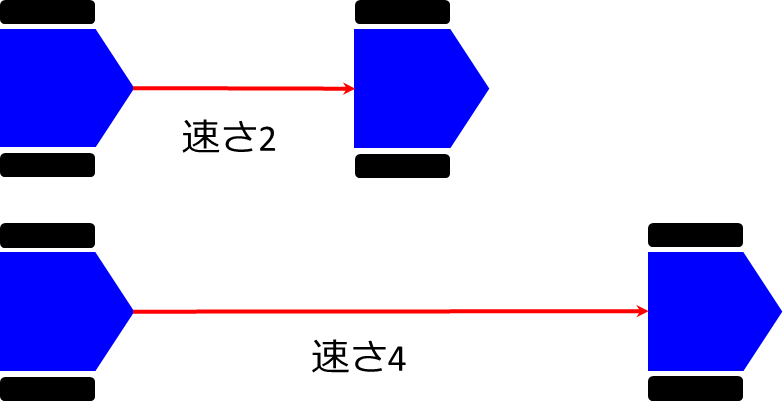
\(velocity(v,\omega)\)
これは、最も単純で速度をそのまま評価値とします。つまり、速度が遅いよりは速い方を評価するということです。下図のような状況だったら、下の方が高く評価されます。
以上をまとめると、ゴール方向を向いていて、障害物から距離がとれ、スピードが速い\((v,\omega)\)が選択されるということになります。
DWAの課題
DWAを用いる際には、複数の静的なパラメータを事前に設定する必要があります。これらには、ロボットの速度、加速度、角速度、角加速度の仕様に基づく値や、予測ステップ数、評価関数\(G\)の計算に用いる重み係数\(\alpha, \beta,\gamma\)などが含まれます。
ロボットの物理的仕様に基づく値は変更できない一方で、予測ステップ数や重み係数は調整可能であり、これらの調整によってDWAの挙動に大きな影響を与えることができます。たとえば、予測ステップ数を変更すると、予測経路の長さが変わります。予測経路が長い場合、早期に大きく回避動作を取ることで、最短経路から大きく外れる経路を選択する傾向があり、目標地点に効率的に到達できない可能性があります。一方、予測経路が短い場合は、障害物を直前で回避する動作が増え、比較的最短経路をたどる傾向にありますが、障害物の配置によってはリスクが高まることもあります。このため、適切なパラメータ設定が必要です。
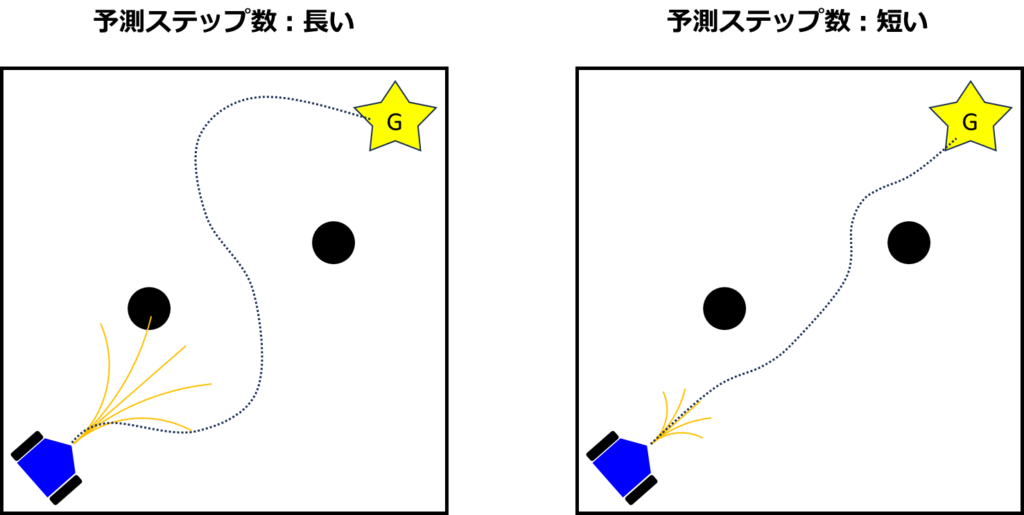
さらに、DWAでは評価関数による評価時に障害物を静止しているものとして扱うため、人間などの移動障害物への対応が課題となります。この問題に対処するために、DWAを強化学習と組み合わせるアプローチが検討されています。

DWAと強化学習の融合による移動障害物回避
DWAと強化学習(RL)を組み合わせた移動障害物回避手法、特にDWA-RL[2]について簡単に紹介します。この手法は、DWAに基づいて生成された速度と角速度の組み合わせ\((v,\omega)\) およびその評価値を利用し、これらを方策の入力として利用することにより、ロボットの局所的なパスプランニングを強化学習で最適化します。具体的には、Observation Space Generationと呼ばれるプロセスにおいて、DWAを用いて評価値と共に速度と角速度の組み合わせを時系列データとして整理し、これを強化学習モデルの入力とします。
従来の強化学習のみを用いたローカルパスプランニング手法では、急激な値の変化や不自然な動きがしばしば観察されました。しかし、DWA-RLでは、DWAによって生成された組み合わせから選択することで、より自然な動きを実現し、移動障害物を含む動的な環境下でも効果的に対応可能な動きを導き出すことが可能です。
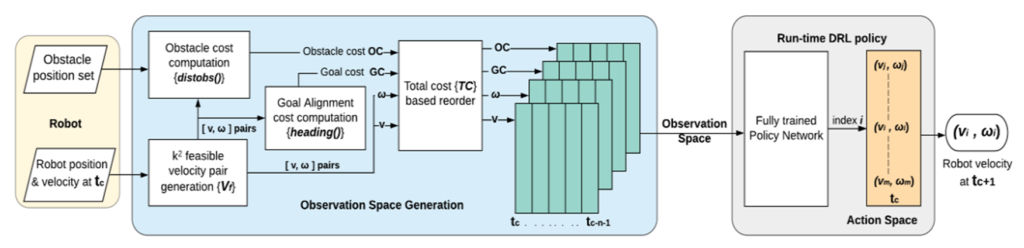
このDWA-RL手法は、少々複雑なプロセスを含んでいますが、この他にも、強化学習による係数調整など、さまざまな革新的なアイデアが提案されています。DWAと強化学習の融合によるこの手法の詳細に興味がある方は、ぜひ色々調べてみて下さい。まだまだ沢山の手法があります。
まとめ
本記事では、移動ロボットのローカルパスプランニングに広く用いられるDynamic Window Approach(DWA)と、それを強化学習(RL)と組み合わせたアプローチについて解説しました。DWAは、ロボットが実行可能な速度と角速度の範囲内で最適な経路を選択することにより、効率的かつ安全な障害物回避を可能にします。しかし、この方法には複数の静的パラメータを事前に設定する必要があったり、移動障害物には対応できないなどの課題も存在します。
DWAの核心部分には、速度\(v\) と角速度\(\omega\) の範囲を動的に調整する「Dynamic Window」の概念があり、これによりロボットの物理的制約と環境の変化に柔軟に対応することが可能です。評価関数\(G(v,\omega)\)は、ロボットの進行方向、障害物との距離、および速度を考慮して最適な経路を選択する際に使用します。
さらに、DWAの課題を強化学習で補おうとするアプローチが登場しており、それらは移動障害物回避などへの対応が可能となることが期待されます。
参考文献
[1] D. Fox, W. Burgard, and S. Thrun, “The Dynamic Window Approach to Collision Avoidance,” IEEE Robotics & Automation Magazine, 1997.
[2] Utsav Patel, Nithish K Sanjeev Kumar, Adarsh Jagan Sathyamoorthy, and Dinesh Manocha, “DWA-RL: Dynamically Feasible Deep Reinforcement Learning Policyf or Robot Navigation among Mobile Obstacles,” in Proc. ICRA, 2021.
