今回は、制約ボルツマンマシンについて説明していきたいと思います。今回説明する内容は、ボルツマンマシン(BM)から制約ボルツマンマシン(RBM)へ、コントラスティブ・ダイバージェンス(CD)法、制約ボルツマンマシンが使用されるところ、プログラムコードの例です。
当サイトはTwitterやYouTubeでも情報発信しています。ご気軽にフォロー(@AGIRobots)、チャンネル登録お願いします!
動画での解説もしています!
ボルツマンマシン(BM)から制約ボルツマンマシン(RBM)へ
以前の記事で、ボルツマンマシンは隠れ変数(隠れニューロン)を持つかどうかで2種類に大別できることを説明しました。制約ボルツマンマシンでは、隠れ変数をもつボルツマンマシンに注目して、その結合に制約を加え、階層的なニューラルネットワークとして考えたものになります。
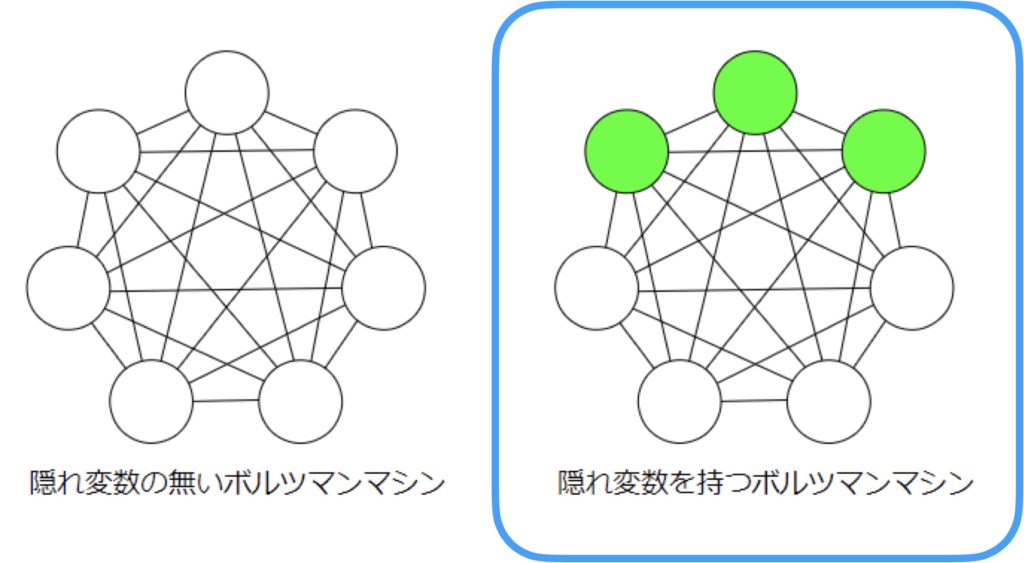
具体的な制約は、可視ニューロン同士、隠れニューロン同士は重み結合を持ってはいけないというものです。つまり、情報のやり取りは、可視ニューロンと隠れニューロン間でのみ成立します。
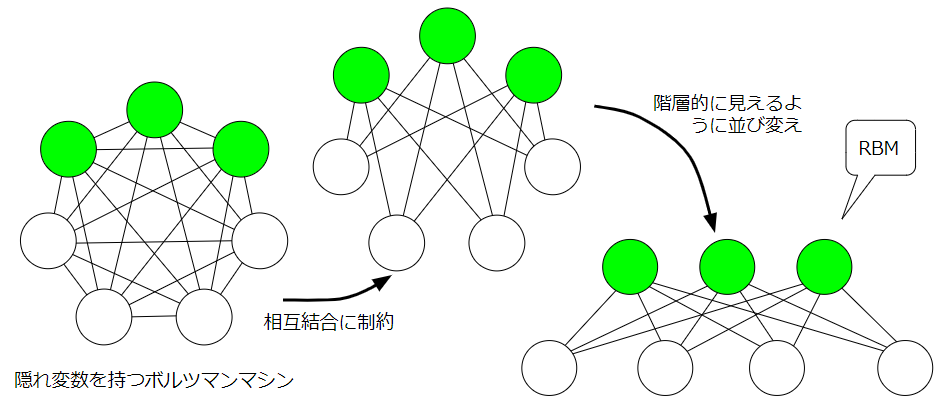
コントラスティブ・ダイバージェンス法の前に
次に、制約ボルツマンマシンの学習方法としてのコントラスティブ・ダイバージェンス法について説明する前に、なぜコントラスティブ・ダイバージェンス法が使用されるのかについて、コントラスティブ・ダイバージェンス法を使用しない場合の問題点について説明したいと思います。
ボルツマンマシンの学習について思い出してみると、対数尤度の最大化という最適化問題を勾配法を使用して近似的に解きました。
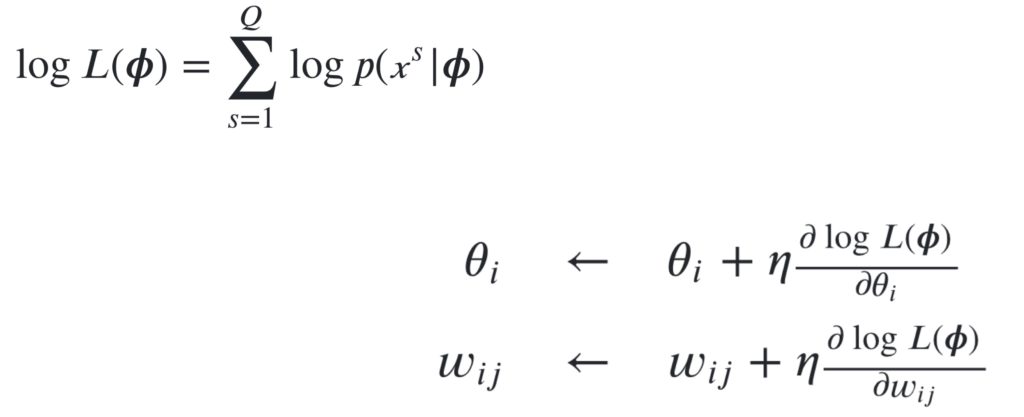
ただし、この場合、勾配を求める際の計算において、組み合わせ爆発が発生してしまうという問題が起こりました。ですので、この勾配の部分を近似的に求める術はないかといアイディアが浮かびます。ただ、全てのニューロンが相互結合しているボルツマンマシンでは、近似的に簡単に解決する方法がなかなか見つからないのですが、制約ボルツマンマシンでは、可視変数内及び隠れ変数内の相互結合がないので、完全に階層的に計算が行え、計算量の少ない良い学習方法としてコントラスティブ・ダイバージェンス法が見つけ出されました。
コントラスティブ・ダイバージェンス法
コントラスティブ・ダイバージェンス(Contrastive Divergence:CD)法とは、上で説明したように、重みやバイアスを更新する量を近似的に求める方法です。計算のイメージを以下に示します。以下の図は、最低限の計算手順で、これはTステップに拡張して考えることができます。
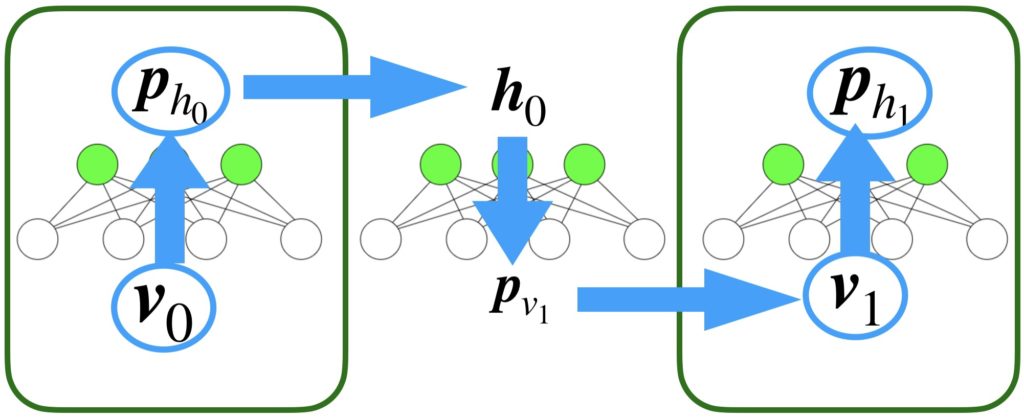
まず、最初に、0-1の値をもつ入力行列(バッチデータなら)もしくは入力行列を\(\boldsymbol{v}_0\)を可視変数に入力します。そして、その値から、隠れ層の各ニューロンが1を出力する確率\(\boldsymbol{p}_{h_0}\)を求めます。確率に変換するときは、ボルツマン分布を使用しますが、基本的に温度係数1のロジスティック関数に入力します。これにより求まった確率を使用してサンプリングを行います。サンプリングの結果、隠れ層の各ニューロンの実際の0-1値\(\boldsymbol{h}_0\)が求まります。今度は、この値を使用して可視層の値\(\boldsymbol{p}_{v_1}\)を求めます。これは確率なので、先ほどと同じ手順でサンプリングを実行し、実際のバイナリ値\(\boldsymbol{v}_1\)を求めます。その後、\(\boldsymbol{p}_{h_1}\)を求めます。ここで最も単純なCD法では、\(\boldsymbol{v}_0\)、\(\boldsymbol{p}_{h_0}\)、\(\boldsymbol{v}_1\)、\(\boldsymbol{p}_{h_1}\)に注目して重みの更新量を決定します。
その具体的な計算方法を以下に示します。
$$\begin{eqnarray}
\boldsymbol{W} &=& \boldsymbol{W} + \eta(\boldsymbol{v}_0^T\boldsymbol{p}_{h_0} - \boldsymbol{v}_1^T\boldsymbol{p}_{h_1})\\
\boldsymbol{h_b} &=& \boldsymbol{h_b} + \eta(\langle\boldsymbol{v}_0\rangle - \langle\boldsymbol{v}_1\rangle)\\
\boldsymbol{v_b} &=& \boldsymbol{v_b} + \eta(\langle\boldsymbol{p}_{h_0}\rangle - \langle\boldsymbol{p}_{h_1}\rangle)\\
\end{eqnarray}$$
重みは行列、学習係数はスカラー、その他は行列もしくは行ベクトルを想定しています。隠れ層のニューロンのバイアスと可視層のニューロンのバイアスの更新量は行ベクトルでないといけないので、例えば\(\boldsymbol{v}_0\)なら、バッチサイズに渡り同じニューロンの出力に対して平均をとることで、行ベクトル\(\langle\boldsymbol{v}_0\rangle\)にして計算しています。
制約ボルツマンマシンが使用されるところ
制約ボルツマンマシンは、協調フィルタリングによる推薦システムなどで使用されます。
プログラム例
プログラムを作成してみましたので、以下に示します。最も単純なCD法をそのまま実装しただけです。
import numpy as np
class RBM():
def __init__(self, v_num, h_num):
"""
=引数=
v_num:可視ニューロンの数
h_num:隠れニューロンの数
=重みパラメータと状態パラメータの定義=
self.w:可視ニューロンと隠れニューロン間の重み結合を表す行列
self.v_b:可視ニューロンの持つバイアス
self.h_b:隠れニューロンが持つバイアス
self.v:可視ニューロンの状態を表すベクトル
self.h:隠れニューロンの状態を表すベクトル
"""
self.v_num = v_num
self.h_num = h_num
self.w = np.zeros((v_num, h_num), dtype=np.float32)
self.v_b = np.zeros((v_num, ), dtype=np.float32)#.reshape(-1, v_num)
self.h_b = np.zeros((h_num, ), dtype=np.float32)#.reshape(-1, h_num)
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def sampling(self, p):
_s = p - np.random.random_sample(p.shape)
return np.where(0, 1, _s > 0)
def v_to_h(self, x):
"""
可視ニューロンのバイナリ値から隠れニューロンの値を導出
シグモイド関数を使い確率へ写像
入力データの型は[batch_size, feature_num]を想定
"""
return self.sigmoid(x @ self.w + self.h_b)
def h_to_v(self, x):
"""
隠れニューロンのバイナリ値から可視ニューロンの値を導出
シグモイド関数を使い確率へ写像
入力データの型は[batch_size, feature_num]を想定
"""
return self.sigmoid(x @ self.w.T + self.v_b)
def fit(self, x, eta, epochs):
err = []
for epoch in range(epochs):
v0 = x
p_h0 = self.v_to_h(v0)
h0 = self.sampling(p_h0)
v1 = self.sampling(self.h_to_v(h0))
p_h1 = self.v_to_h(v1)
self.w = self.w + eta*(v0.T @ p_h0 - v1.T @ p_h1)
self.v_b = self.v_b + eta*(np.mean(v0, axis=0) - np.mean(v1, axis=0))
self.h_b = self.h_b + eta*(np.mean(p_h0, axis=0) - np.mean(p_h1, axis=0))
err.append(np.mean(np.abs(v0-v1)))
return err
def test(self, x):
v0 = x
h0 = self.sampling(self.v_to_h(v0))
v1 = self.sampling(self.h_to_v(h0))
return v1これにMNISTを学習させてみた時の再構成誤差を以下に示してみます。
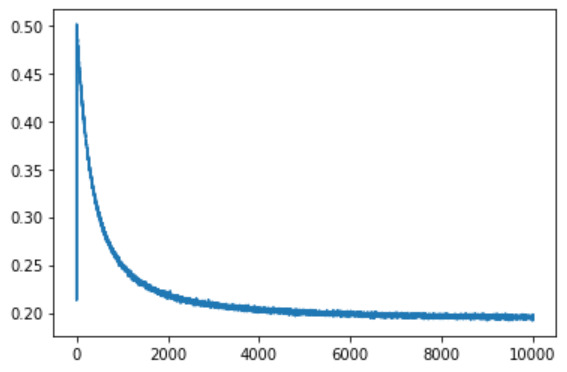
10000エポック実行しました。学習ステップが進むごとに、一応再構成誤差は小さくなっているようなので、おそらくこれでRBMは実装できたって感じでしょうか(;^_^A
本日の内容は以上になります。最後までお読みいただきありがとうございました。
