本日は前回の制約ボルツマンマシンに引き続き、深層信念ネットワークについて説明していきたいと思います。
当サイトはTwitterやYouTubeでも情報発信しています。ご気軽にフォロー(@AGIRobots)、チャンネル登録お願いします!
本記事の解説動画は以下です。
制約ボルツマンマシン(RBM)から深層ボルツマンマシン(DBM)
式の詳細については触れませんが、概要を説明していきたいと思います。
まず、制約ボルツマンマシンについて思い出してみます。制約ボルツマンマシンは可視ニューロン層と隠れニューロン層を持ち、同じ層内のニューロン同士は結合を持たないという制約を持ちました。また、学習はコントラスティブ・ダイバージェンス(CD)法を使用することで、効率的に学習を行いました。
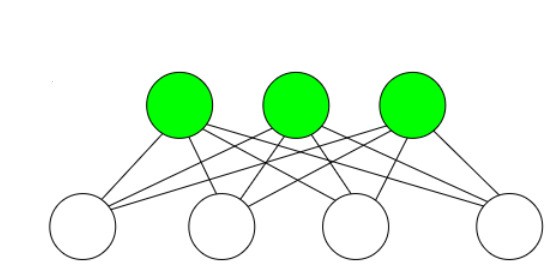
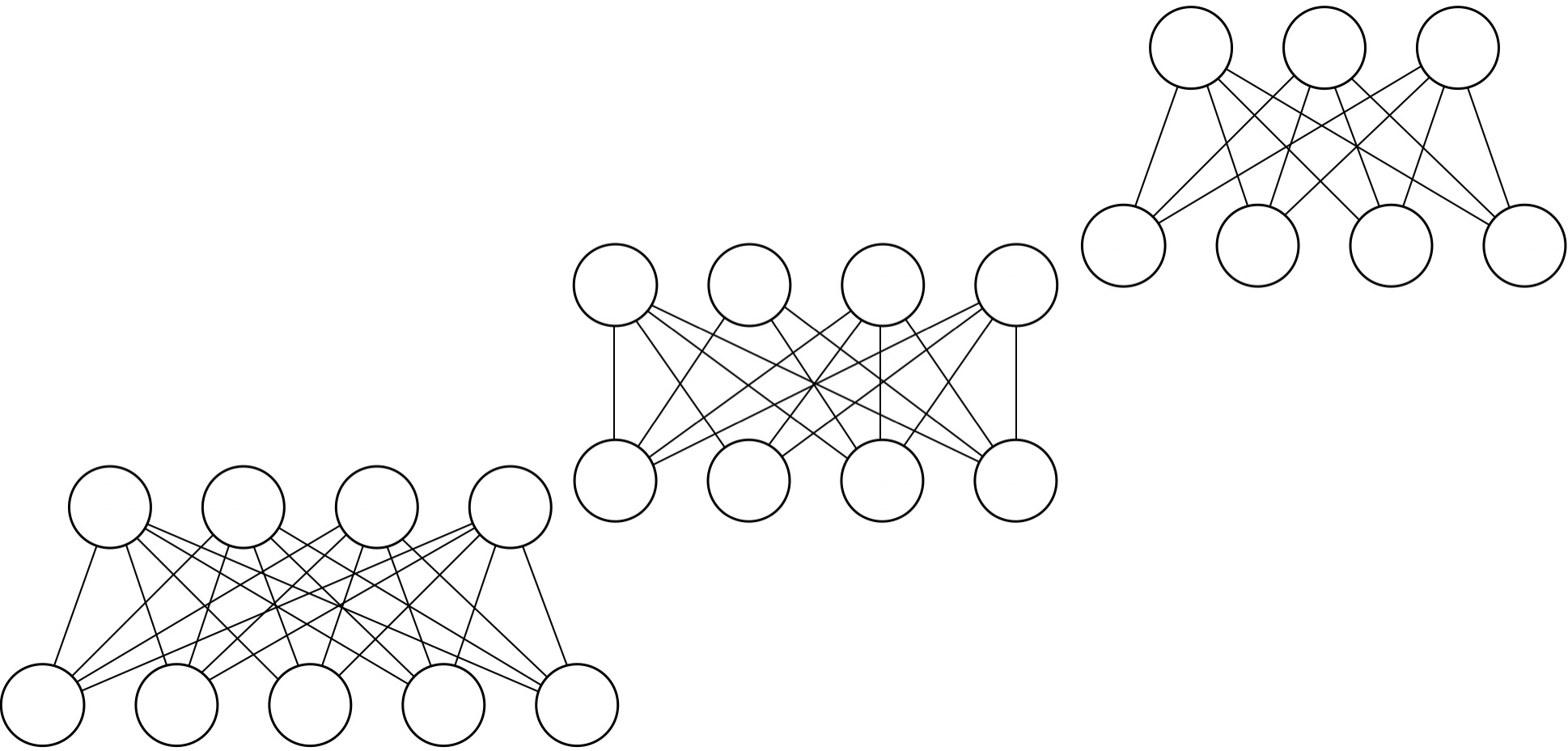
この制約ボルツマンマシンを複数スタックし、深層にしたらどうなるでしょうか?以下の図では3つの制約ボルツマンマシンを用意しました。
これをスタックし多層にすると、以下のようになります。これが深層ボルツマンマシン(DBM)です。これは、全てが無効グラフで繋がれており、学習は難しいです。
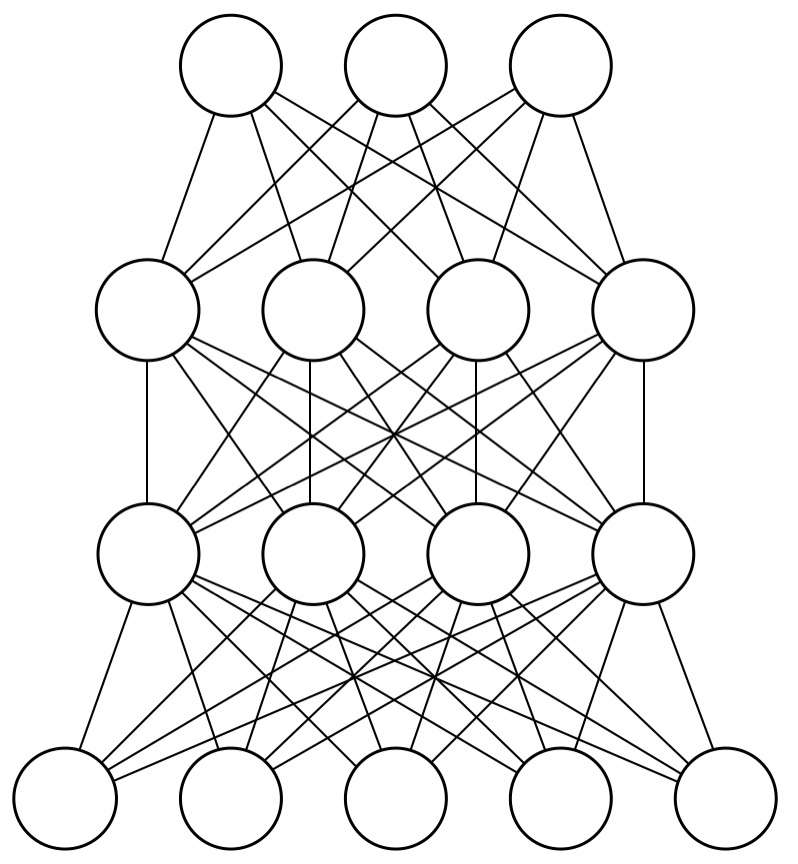
深層ボルツマンマシン(DBM)から深層信念ネットワーク(DBN)
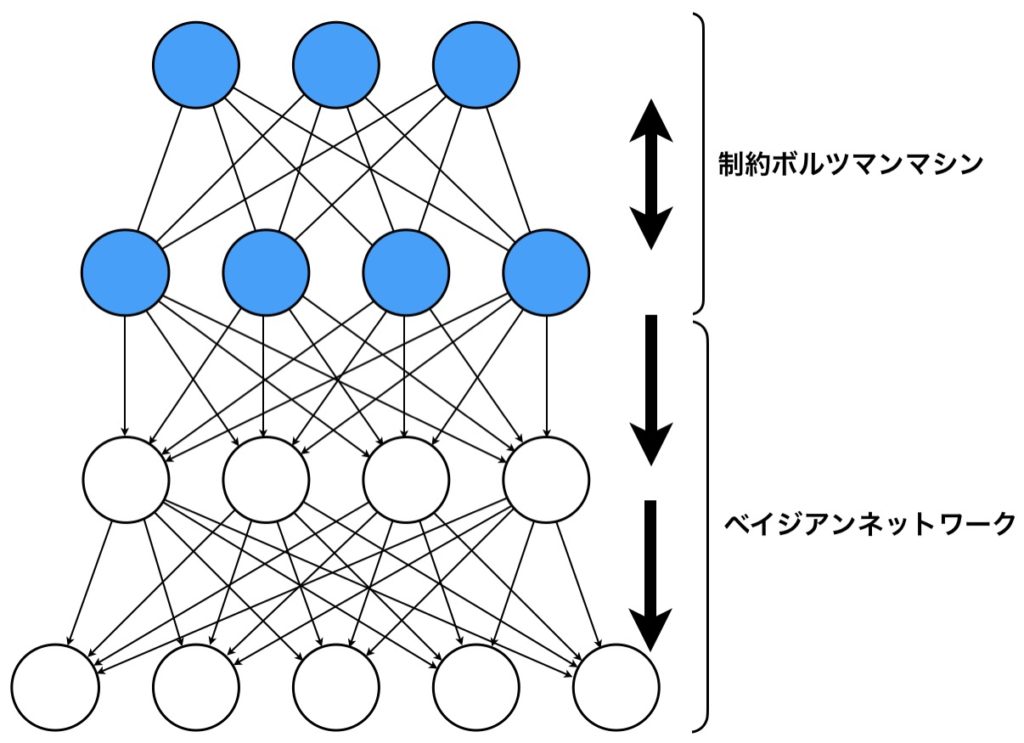
いま、深層ボルツマンマシンについて触れましたが、ここで、最も深層な部分のみ制約ボルツマンマシンにし、それ以外は有向なベイジアンネットワークにしたらどうでしょうか?
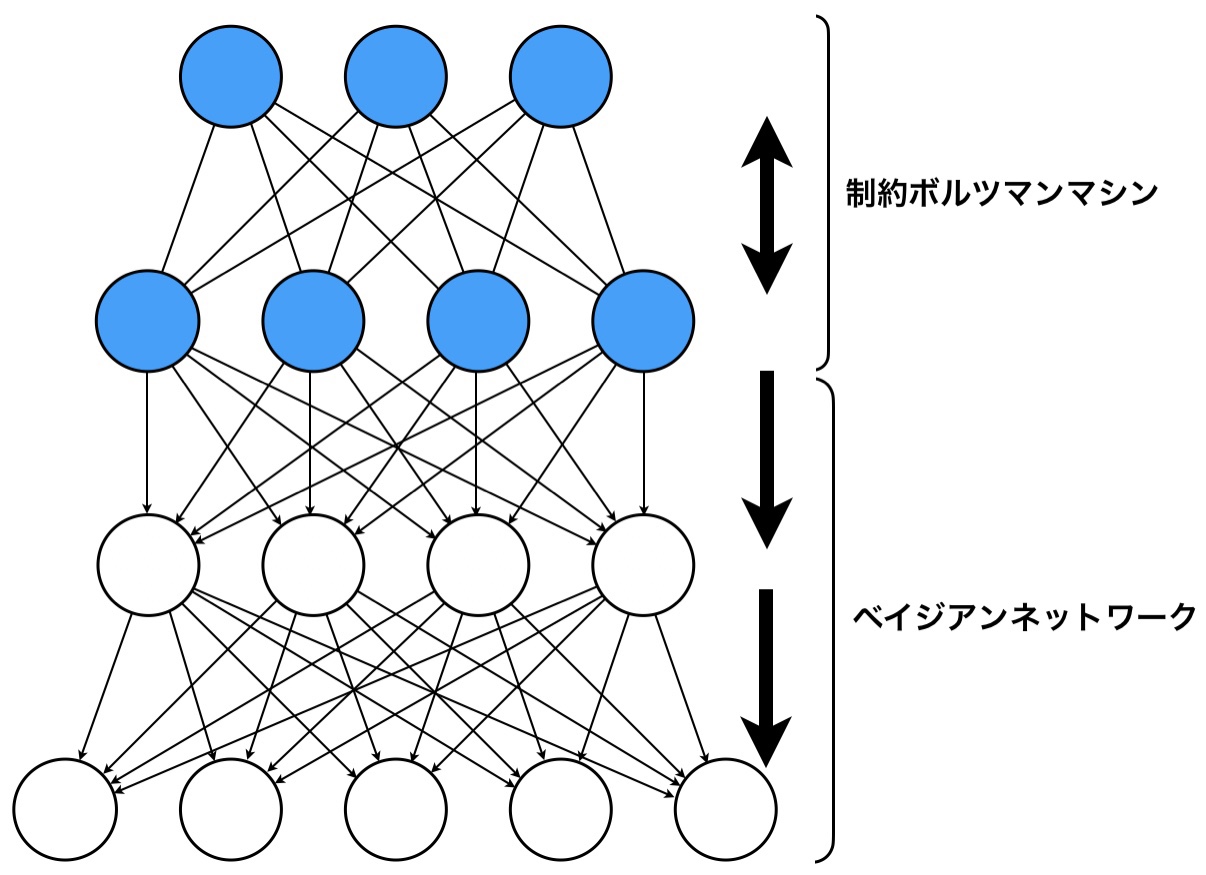
これが深層信念ネットワーク(DBN)です。DBNの特徴は、制約ボルツマンマシンとベイジアンネットワークで構成されること、各ニューロンは確率ニューロンなので確率的に0か1の値をとるところです。
深層信念ネットワークの学習
DBNの学習について考えたいと思います。まず、可視層に最も近い部分の制約ボルツマンマシンについて考えたいと思います。
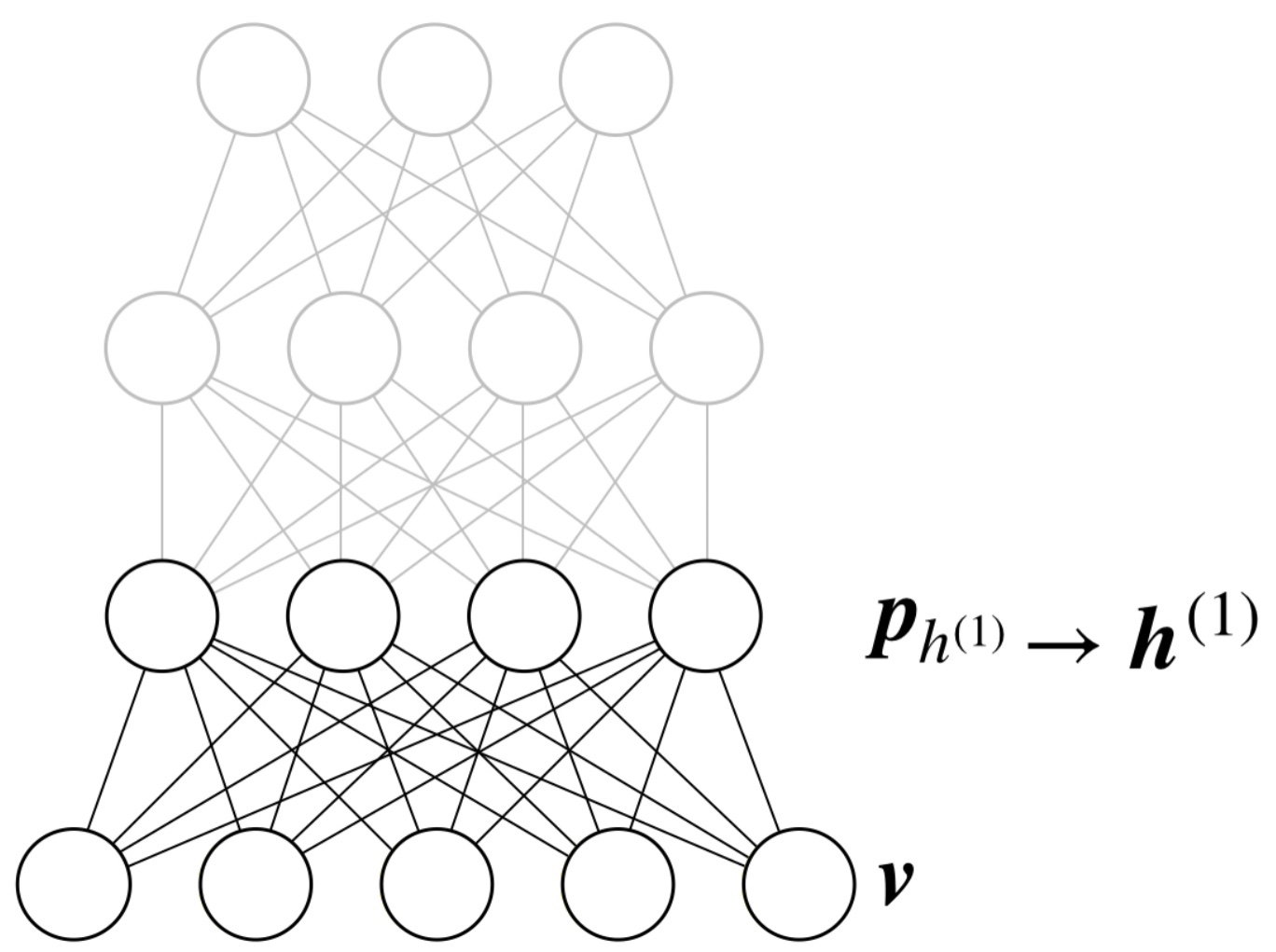
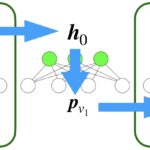
図では、可視層に0-1の値を成分としてもつベクトル\(\boldsymbol{v}\)が入力されています。このとき、線形変換により、層\(h^{(1)}\)の各々のニューロンが1をとる確率\(\boldsymbol{p}_{h^{(1)}}\)を求めます。その確率を使用して0-1の値\(\boldsymbol{h}^{(1)}\)にサンプリングします。その後、可視層が1をとる確率\(\boldsymbol{p}_{v1}\)を求め、再度、隠れ変数の値を求め、コントラスティブダイバージェンスを使って学習します。コントラスティブダイバージェンスについては、以下の記事で説明しているので、ぜひご覧ください。
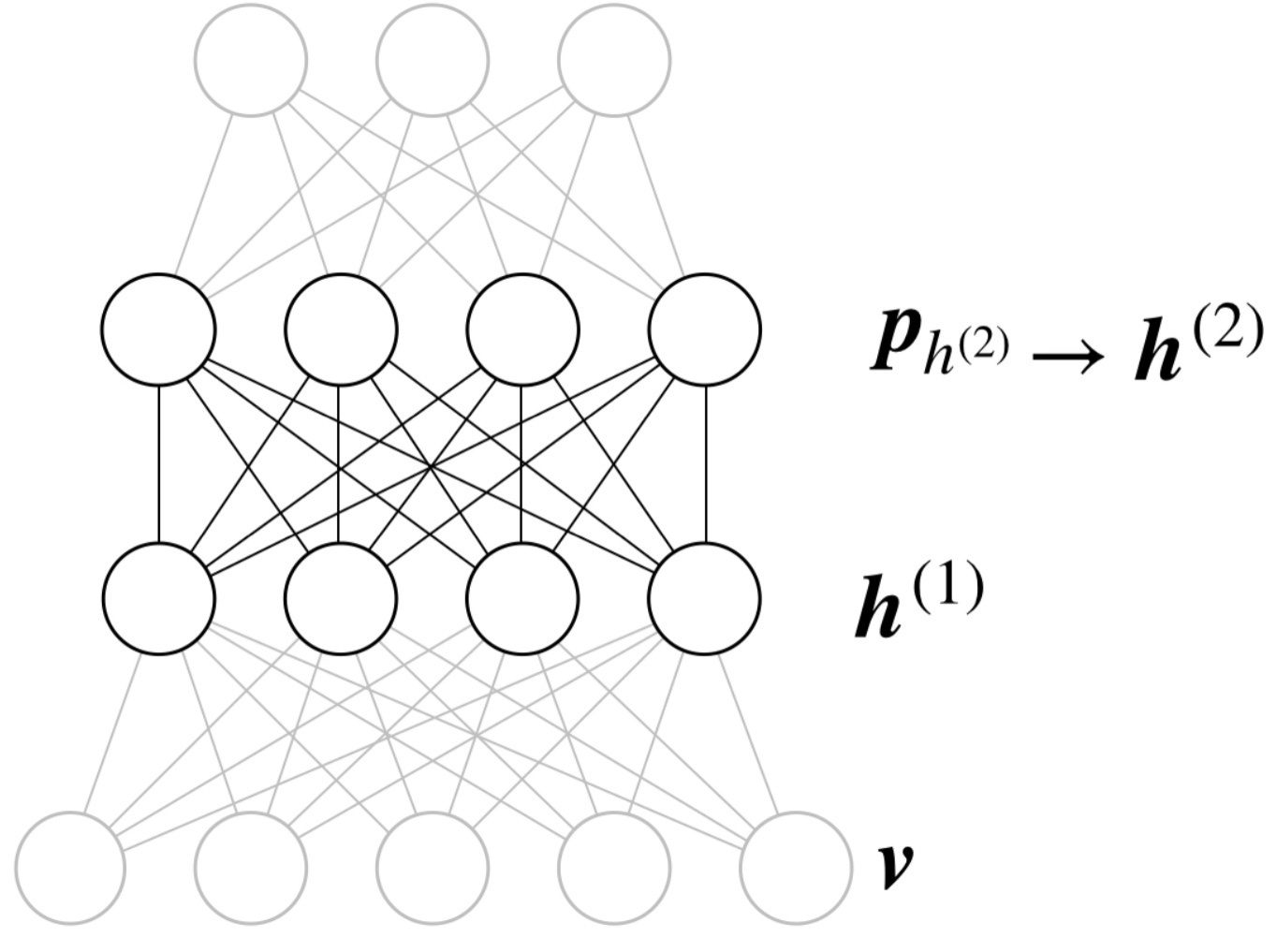
1つ目の制約ボルツマンマシンの学習ができたら、その制約ボルツマンマシンの値を固定し、次の制約ボルツマンマシンを学習します。その際には、先ほど隠れ層として考えていた層を可視層とし、1つ目の制約ボルツマンマシンの隠れ層の値が再構成できるようにコントラスティブダイバージェンスを使って学習します。
深層信念ネットワークは生成モデル
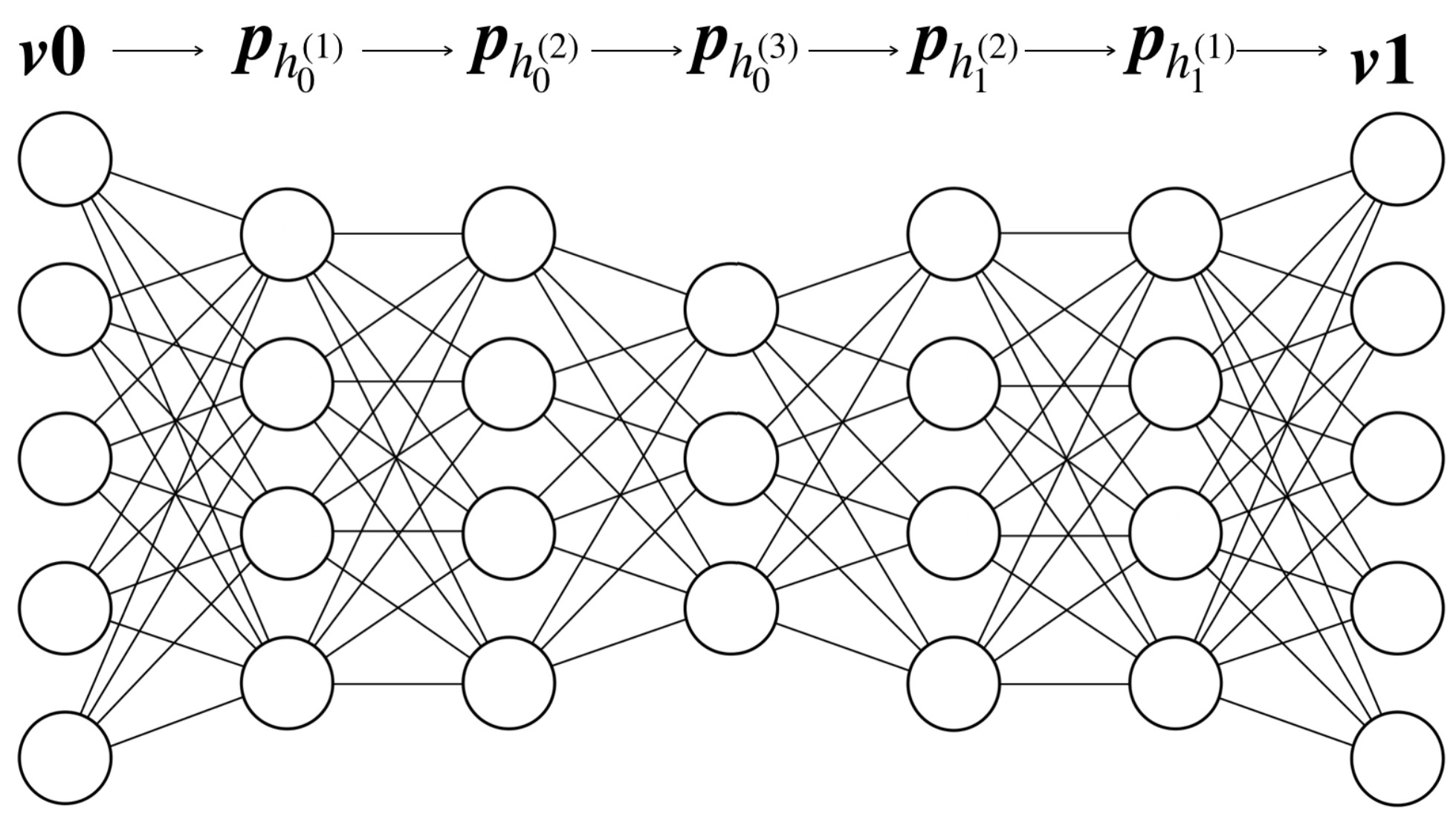
ここまで簡単に説明してきましたが、DBNは生成モデルであることを説明したいと思います。以下の図は正確にはDBNではありません(DBNは制約ボルツマンマシンとベイジアンネットワークからなるので)が、これを使って、データがどのように再構成されるか追ってみたいと思います。
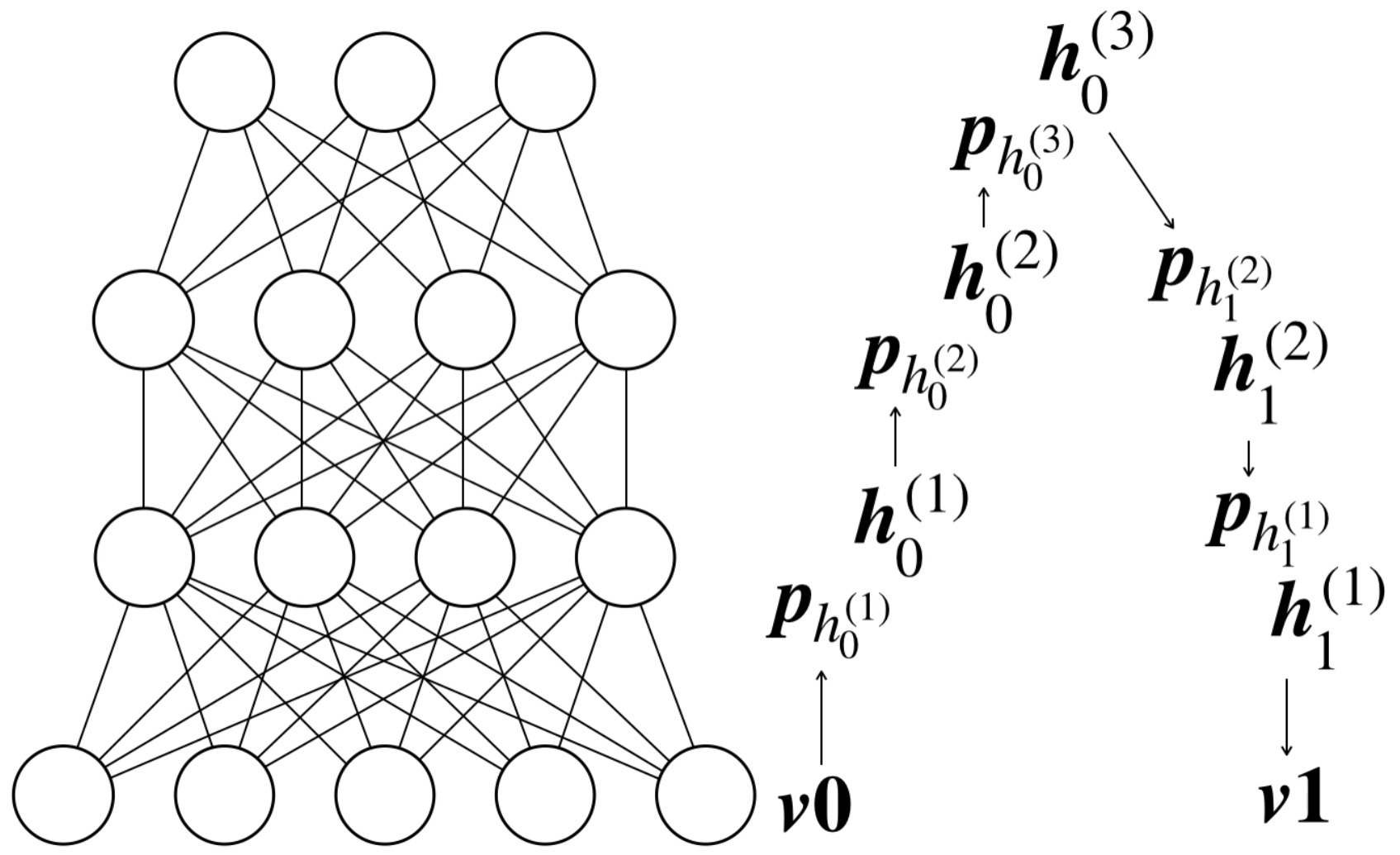
まず、入力データとして\(\boldsymbol{v0}\)が可視層に与えられます。そこから、1つ目の隠れ層にある各ニューロンが1を出力する確率\(\boldsymbol{p}_{h_0^{(1)}}\)を求め、サンプリングをして実際の出力状態\(\boldsymbol{h_0}^{(1)}\)を求めます。次に、\(\boldsymbol{h_0}^{(1)}\)を入力として、2つ目の隠れ層のニューロンが1を出力する確率\(\boldsymbol{p}_{h_0^{(2)}}\)を求め、サンプリングして実際の出力状態\(\boldsymbol{h_0}^{(2)}\)を求めます。これを最も深い層まで実施し、折り返して、可視層に戻ってきて再構成されたものを\(\boldsymbol{v1}\)としたいと思います。もし、多層パーセプトロンのような決定的なニューロンを使用して構築されたネットワークの場合、入力\(\boldsymbol{v0}\)が決まれば再構成結果\(\boldsymbol{v1}\)は必ず一意に決まります。しかし、ベイジアンネットワークではボルツマンマシンの特徴である確率的な過程を引き継いでいるので、同じ入力をしても、生成されるものは、毎回微妙に異なるものになります。
再度、最初に示したDBNの図を思い出してみます。この図のDBNはあたかも永遠にデータを生成できるかのように振舞います。図において最も上の層に何らかのノイズを加えれば確率的な過程を経てベイジアンネットワークから何かしらのデータを生成してくれるわけです。例えば、MNISTによる手書き文字を学習したDBNだったら、学習に使用していない手書き文字をたくさん生成できます。
DBNとスタックオートエンコーダ(SAE)の関連性
最後に、DBNとSAEとの関連性について説明したいと思います。DBNでは確率的な離散ニューロンを使っていたので、ここで不確定性を実現し、生成モデルとして振舞っていたのですが、この不確実性を取り除いて、制約ボルツマンマシンの部分の折り返しでパカッと展開すると、以下の図のようなネットワークになります。これはオートエンコーダと同じ形状をしていますね。ただ、オートエンコーダの学習法は誤差逆伝播になりますので、DBNと全く同じではないですが、使われ方としては結構似てると思います。
オートエンコーダはエンコーダとデコーダ部分のネットワークを使って次元圧縮された内部表現を獲得し、エンコーダ部分を取り出して事前学習として使用することが多いです。DBNも同じで、学習した後のネットワークに更に識別器を追加すれば、DBNの部分は特徴抽出部として使用されていることになります。
ここでは深く触れませんでしたが、深層信念ネットワークは深層ニューラルネットワークの学習を始めて可能にしたブレイクスルーで、現在の深層学習の父ということができます。DBN自体は学問的にとても面白いと思うので、また別の機会に触れることができればと思っています。
という感じで、今回の記事を終わりにさせていただきます。最後までお読みいただきありがとうございました。