本記事から数回は、本格的な多層パーセプトロン(MLP)クラスを機械学習ライブラリ(TensorFlow, Keras, PyTorchなど)を使用せずに、NumPyだけを使って実装していきたいと思います。今までは連想記憶のモデルから解説してきたので、急に多層パーセプトロンに話題が飛びましたが、それは連想記憶の話だけで深層学習へ説明を発展させるのは難しいと考えるからです。ましてや深層学習のもう1つの起源である多層パーセプトロンを抜きに先に進むのは不可能に近いです。
さて、多層パーセプトロンは機械学習ライブラリを使用すれば、ほんの数行で実現できます。しかし、その裏には深層学習全般に共通する重要な理論が見えないよう上手に組み込まれていることを忘れるわけにはいきません。
そこで、今回から何回かに分けて、「誤差逆伝播法の理論&導出」、「活性化関数の種類と微分」、「NumPyによる本格的な多層パーセプトロンクラスの実装」、「発展的話題」について扱っていきたいと思います。
本記事は「誤差逆伝播法の理論&導出(決定版)」として、多層パーセプトロンの紹介、勾配降下法の紹介、誤差逆伝播の一般化した式の導出、行列計算による誤差逆伝播の実現、発展的話題として、交差エントロピーとソフトマックス関数による誤差逆伝播に焦点をあてて説明していきたいと思います。計算自体は、学部生レベルの微積分、線形代数が理解できれば大丈夫な内容です。
多層パーセプトロンとは
多層パーセプトロンとは現在のニューラルネットワークの原形を成すもので、全結合型フィードフォワードニューラルネットワークです。多層パーセプトロンは以下のような図で表されます。図から分かるように、沢山のニューロンが階層的に配置されていて、入力層、連合層(隠れ層、中間層ともいう)、出力層からなります。情報は低次の層から高次の層へと移動します。また、多層パーセプトロンは入力データと教師データの関係を誤差逆伝播による誤り訂正学習により反復的に学習します。
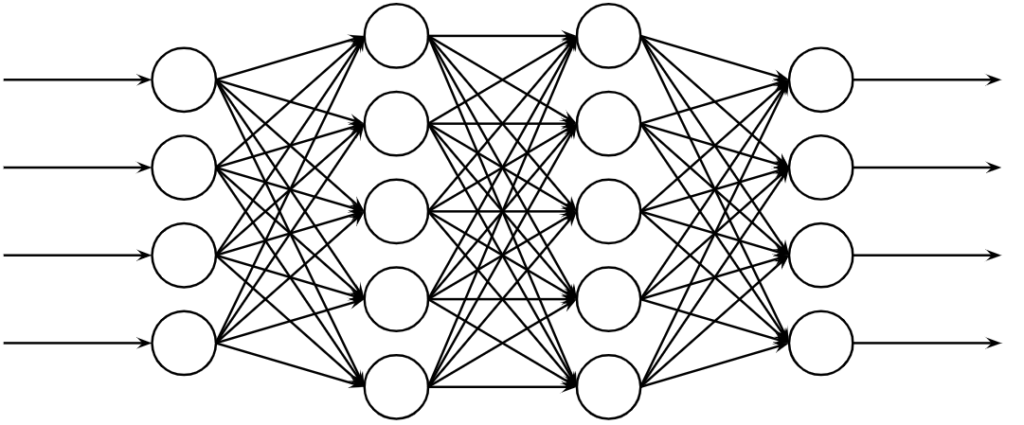
多層パーセプトロンの計算は、順方向と逆方向の2つに大別され、順方向に関してはご存じの方が多いと思いますので割愛し、逆方向の計算である誤差逆伝播の説明に重点を置いて説明をしていきます。
最適化問題と勾配法と誤差逆伝播法
まず最初に勾配法と誤差逆伝播法の位置づけを最適化問題と絡めて説明したいと思います。
最適化問題と勾配法
最適化問題とは制約条件を満たす実行可能解\(\boldsymbol{x}\)の集まりである実行可能集合\(\boldsymbol{S}\)から、目的関数\(J(\boldsymbol{x})\)を最大化もしくは最小化する実行可能解、すなわち最適解を求める問題をいい以下のような一般形で表されます。
$$\begin{eqnarray}
\mbox{目的関数}&:&J(\boldsymbol{x})\\
\mbox{制約条件}&:&\boldsymbol{x}\in \boldsymbol{S}
\end{eqnarray}$$
ニューラルネットワークの学習は、上記のような最適化問題に帰着させることで実現します。ニューラルネットワークの場合、実行可能解はネットワークの重みになります。最適化問題は解析的に求める方法と近似的に求める方法がありますが、ニューラルネットワークはとても複雑なので解析的に解くのは困難です。そこで、近似的に手探りで解く方法として勾配法が使用されます。勾配法には勾配上昇法と勾配降下法があり、目的関数の最大化では勾配上昇法が、最小化では勾配降下法が使用されます。とはいえ、最大化問題と最小化問題は符号変換することで入れ替えることができるので、一般的には目的関数の最小化問題で標準化し勾配降下法で解析的に解くのが一般的です。以下に勾配上昇法と勾配降下法のそれぞれの重み更新式を示します。
$$\begin{eqnarray}
\mbox{勾配上昇法}&:&\boldsymbol{w}\leftarrow \boldsymbol{w}+\eta\nabla J(\boldsymbol{w})\\
\mbox{勾配降下法}&:&\boldsymbol{w}\leftarrow \boldsymbol{w}-\eta\nabla J(\boldsymbol{w})
\end{eqnarray}$$
勾配上昇法では勾配を上る方向に重みパラメータを更新します。逆に勾配降下法では勾配を下る方向に重みパラメータを更新します。
勾配法と誤差逆伝播法
勾配法では、更新したいパラメータの更新量を目的関数の勾配として計算します。階層的な構造を持つニューラルネットワークでは、勾配が出力層側から入力層側へ順番に計算されます。これは、入力層から出力層へ情報が伝播する順伝播とは逆方向へ勾配が求まっていくことから、誤差逆伝播法といわれます。
誤差逆伝播法の考え方(←ここ超重要!!!)
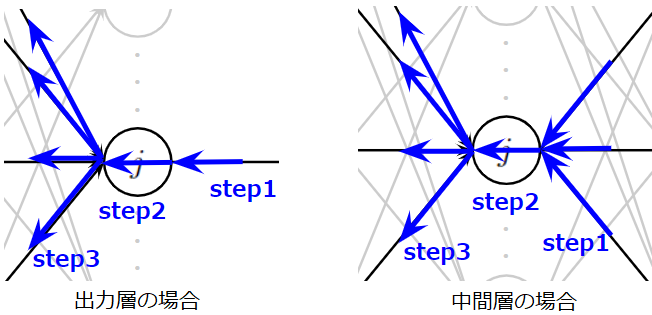
とても難しく複雑そうに見える誤差逆伝播ですが、基本的には次に示す3ステップで説明できます。
- (Step1):\(j\)番目に逆伝播されてくる誤差の合計値を計算
- (Step2):Step1の誤差の合計値は\(j\)番目のニューロンの出力時のスケールなので入力時のスケールに変換
- (Step3):\(j\)番目のニューロンに入力された入力値の大きさに応じて平等に誤差を分配
この3ステップをイメージしやすいように以下にアニメーションを作成しました。\(j\)番目のニューロンが上の層からの誤差を集約し(Step1)、変換し(Step2)、下の層へ分配(Step3)している様子をご理解いただけると思います。
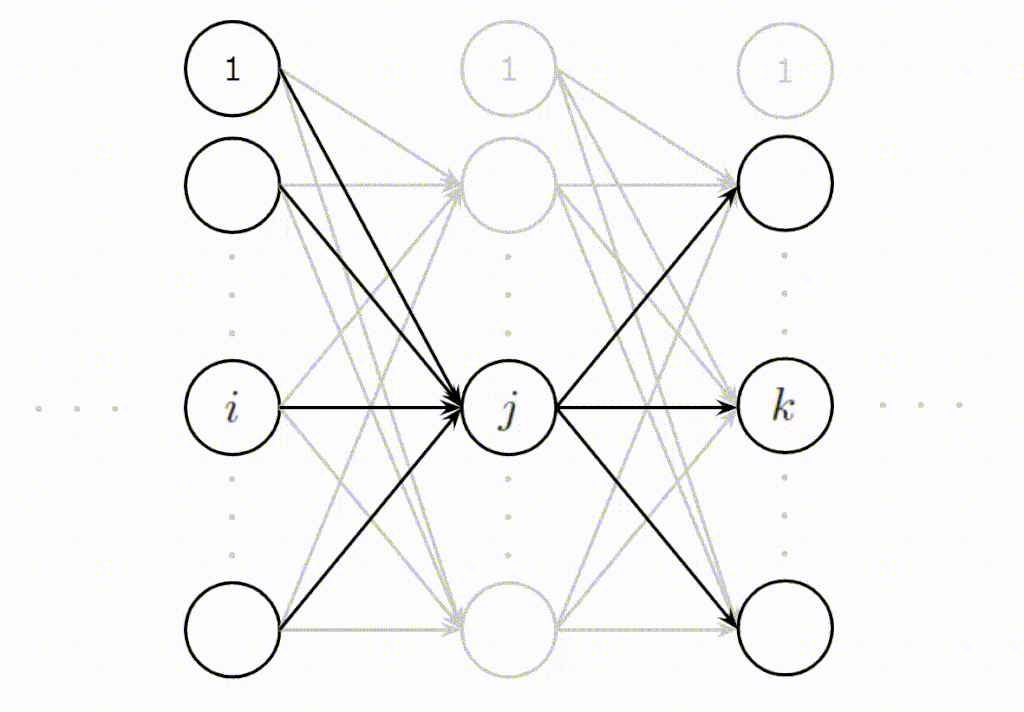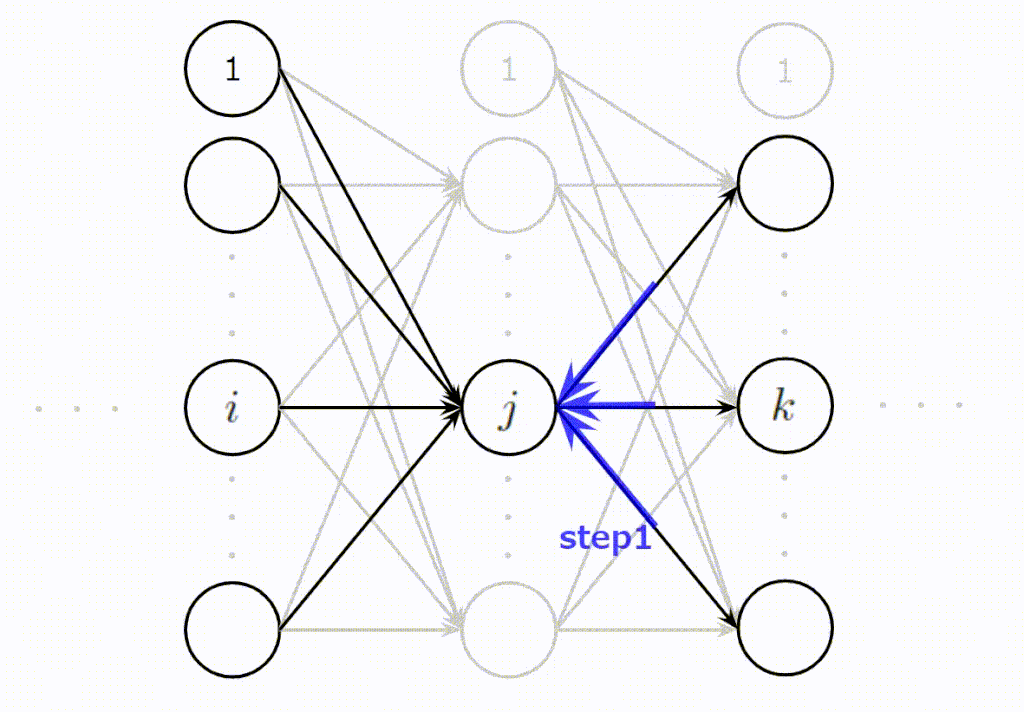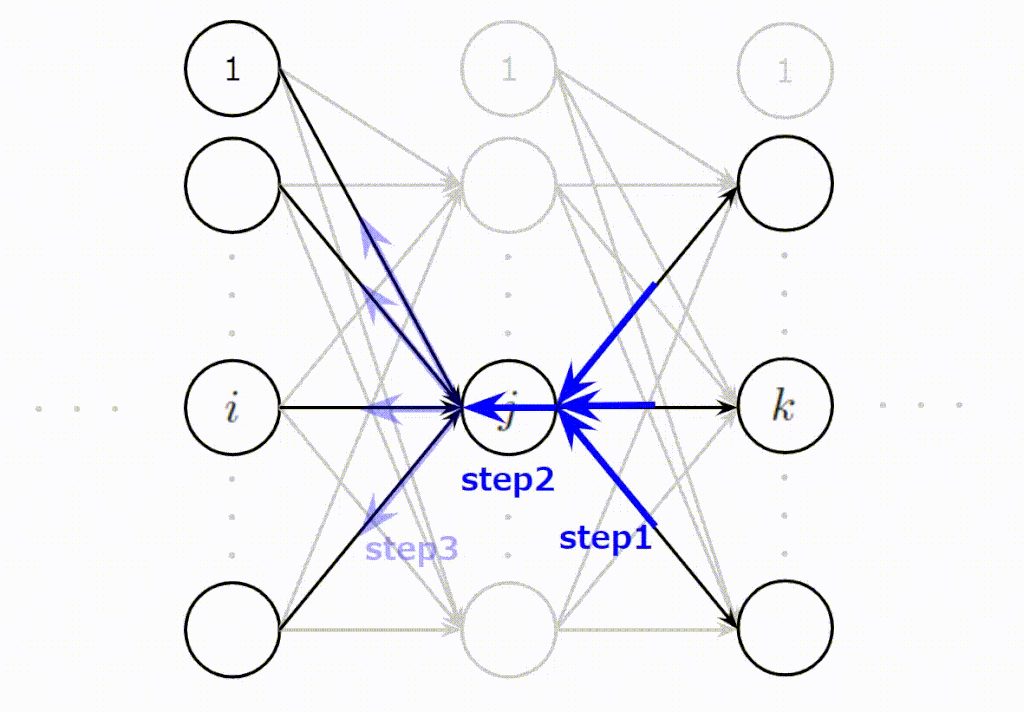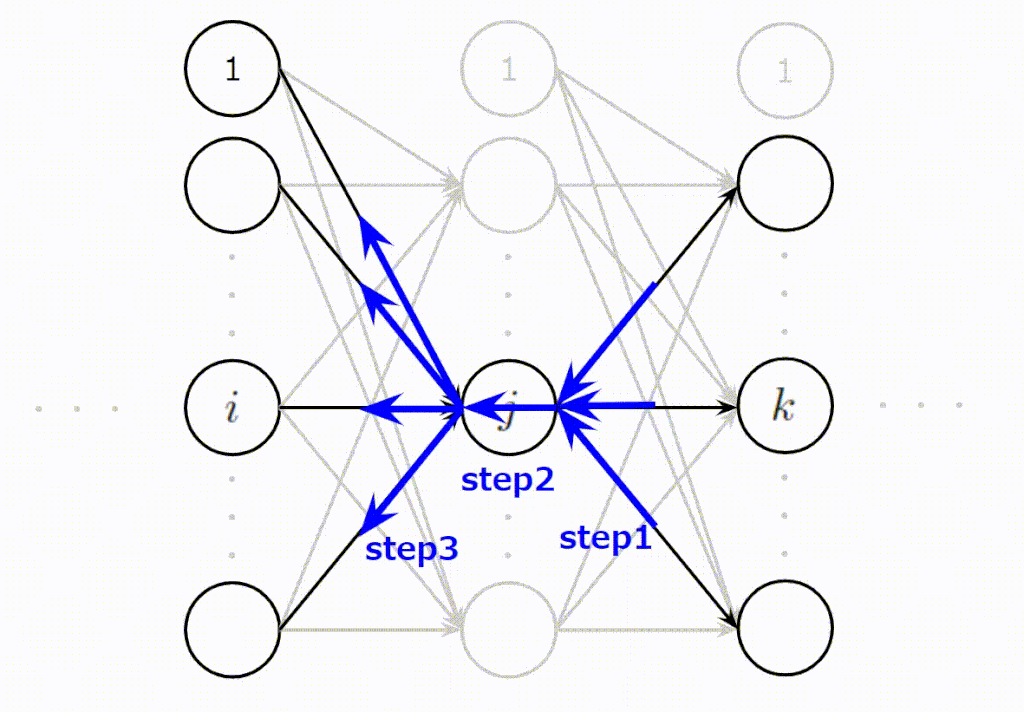
誤差逆伝播法を導出
誤差逆伝播法の式を導出する際に、、以下のようなステップを踏みたいと思います。
- 入力データと教師データの形式を決める
- ニューラルネットワークの形状とパラメータの形状を決める
- 出力層と中間層の結合重みの誤差逆伝播を導出
- 行列を使用した式で定式化
入力データと教師データの形式を決める
誤差逆伝播法の数式を定式化する前に入力データと出力データの形状を決めます。ここで、多くの学習課題に適用可能な入出力の行列の形式を決めることで、汎用的なモデルを定義することが可能になります。ここでは入力、出力、教師データの形式を以下のように定めました。
1つの入力データ、出力データ、教師データはそれぞれ列ベクトル\(\boldsymbol{x}\)、\(\boldsymbol{y}\)、\(\boldsymbol{t}\)とし、バッチサイズ\(N\)でバッチ処理をする際は、これらを横に並べた行列\(\boldsymbol{X}=(\boldsymbol{x_1x_2x_3\cdots x_N})\)、\(\boldsymbol{Y}=(\boldsymbol{y_1y_2y_3\cdots y_N})\)、\(\boldsymbol{T}=(\boldsymbol{t_1t_2t_3\cdots t_N})\)で行列計算をするものとする。
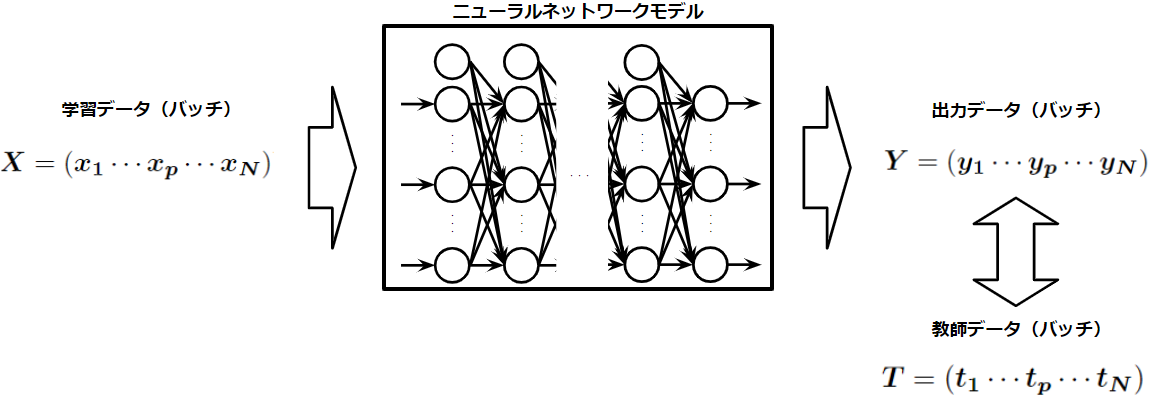
いま説明したものを図示すると上のようになります。
ニューラルネットワークの形状とパラメータの形状を決める
次に、ニューラルネットワークの形を決めます。今回は以下のような多層パーセプトロンを考えます。前層にバイアスニューロンを用意しています。このようにすることで、「重み行列によるアフィン写像+活性化関数による非線形写像」を繰り返す自由度の高いモデルを考えることがができます。
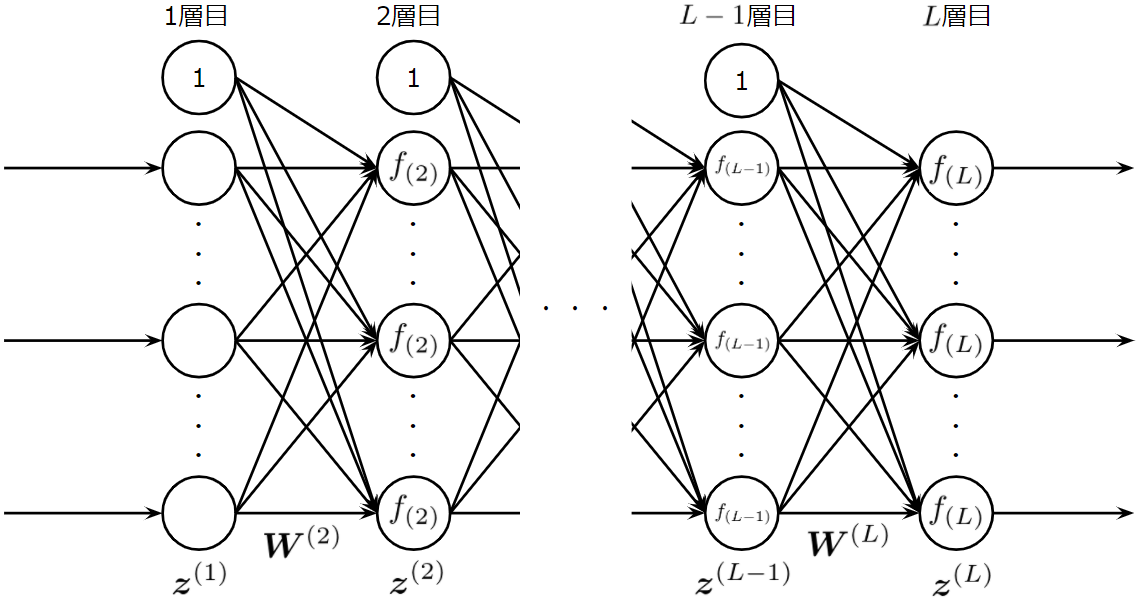
ニューラルネットワークの形状を決めたら、入力データや教師データの形式なども考慮して、各層の出力と重み行列を文字で置きます。ここでは、\(l\)層目の出力を\(\boldsymbol{z}^{(l)}\)、\(l\)層目に繋がっている辺の重み行列を\(\boldsymbol{W}^{(l)}\)とします。入力データや教師データの行列は任意の列が任意の1つのデータに対応するように定義したので、\(l\)層目の出力\(\boldsymbol{z}^{(l)}\)も列ベクトルとし、また、バッチ処理を考える場合は、バッチデータの中の\(p\)番目のデータが入力されたときの\(l\)層目の出力\(\boldsymbol{z}^{(l)}_p\)を列ベクトルとしてもつ行列\(\boldsymbol{Z}^{(l)}\)を考えていくことにします。重み行列\(\boldsymbol{W}^{(l)}\)は\(l-1\)層目の出力ベクトル(バッチデータなら行列)を\(\boldsymbol{W}^{(l)}\boldsymbol{z}^{(l-1)}\)(バッチデータなら\(\boldsymbol{W}^{(l)}\boldsymbol{Z}^{(l-1)}\))のように線形写像します。
図のような多層パーセプトロンを考えているので、\(\boldsymbol{Z}^{(i)}\)の1行目(プログラムで指定する際は0行目)はバイアスニューロンの出力で常に1です。また、重み行列の1列目(プログラムで指定するときは0列目)の値は\(l\)層目の各々のニューロンのバイアス値を示しています。
図に示されている\(f_{(2)},f_{(L-1)},f_{(L)}\)は、2層目、\(L-1\)層目、\(L\)層目のニューロンの活性化関数です。
誤差逆伝播:出力層
ここでは、出力層の誤差逆伝播の式を導出したいと思います。最後に行列形式で一般化したいため、
$$\begin{eqnarray}
\boldsymbol{X}&=&(\boldsymbol{x_1}\cdots\boldsymbol{x_p}\cdots\boldsymbol{x_N})\\
\boldsymbol{Y}&=&(\boldsymbol{y_1}\cdots\boldsymbol{y_p}\cdots\boldsymbol{y_N})\\
\boldsymbol{T}&=&(\boldsymbol{t_1}\cdots\boldsymbol{t_p}\cdots\boldsymbol{t_N})
\end{eqnarray}$$
のようにバッチ形式の入力、出力、教師データを考えたいと思います。ここで、\(p\)番目の入力列ベクトル、出力ベクトル、教師ベクトルは\(\boldsymbol{x_p}, \boldsymbol{y_p}, \boldsymbol{t_p}\)、出力層の\(j\)番目のニューロンに注目すると、そのニューロンの出力と教師信号は\(y_{jp}, t_{jp}\)とあらわせます。
出力層のニューロン数を\(N_L\)、出力層からみて1つ前の層のニューロン数を\(N_{L-1}\)(バイアスニューロンも含む)とおくことにします。このとき、出力層の出力\(\boldsymbol{y}_p=f_{(L)}(\boldsymbol{W}^{(L)}\boldsymbol{z}_p^{(L-1)})\)は、
$$\begin{eqnarray}
\boldsymbol{y}_p&=&f_{(L)}(\boldsymbol{W}^{(L)}\boldsymbol{z}_p^{(L-1)})\\
&=&f_{(L)}\left\{\left(
\begin{array}{ccccc}
w_{11}&\cdots&w_{1i}&\cdots&w_{1N_{L-1}}\\
w_{21}&\cdots&w_{2i}&\cdots&w_{2N_{L-1}}\\
\vdots&\ddots&&&\vdots\\
w_{j1}&\cdots&w_{ji}&\cdots&w_{jN_{L-1}}\\
\vdots&&&\ddots&\vdots\\
w_{N_L1}&\cdots&w_{N_Li}&\cdots&w_{N_LN_{L-1}}\\
\end{array}
\right)\left(
\begin{array}{c}
1\\
z_{2p}\\
\vdots\\
z_{ip}\\
\vdots\\
z_{N_{L-1}p}
\end{array}
\right)\right\}
\end{eqnarray}$$
となります。ここで、勾配降下法より、\(L-1\)層目の\(i\)番目のニューロンから\(L\)層目の出力層\(j\)番目のニューロンの重み結合値\(w^{(L)}_{ji}\)は以下のように更新します。
$$
w^{(L)}_{ji}\leftarrow w^{(L)}_{ji}-\eta\nabla J(w^{(L)}_{ji})
$$
ここで、\(\nabla J(w^{(L)}_{ji})=\frac{\partial J(w^{(L)}_{ji})}{\partial w^{(L)}_{ji}}\)を誤差逆伝播法で求めますが、まずここでは式を複雑に感じさせないために、確率的勾配降下法適用時の誤差逆伝播による更新式、\(\nabla J_p(w^{(L)}_{ji})=\frac{\partial J(w^{(L)}_{ji})}{\partial w^{(L)}_{ji}}\)を求めていきたいと思います。少しだけ勾配降下法と確率的勾配降下法、コスト関数についてフォローておくと、勾配降下法(もしくは最急降下法)はバッチ処理の場合の計算式で一般化されていて、個々のデータに注目した(バッチサイズが1のときの)勾配降下法は確率的勾配降下法といわれます。このとき、バッチサイズ\(N\)のデータで学習するときの勾配降下法の目的関数は、バッチデータのうち\(p\)番目のデータに注目したときの確率的勾配降下法のコスト関数\(J_p\)を使って、
$$
J = \sum_{p=1}^NJ_p
$$
と表せます。目的関数に二乗誤差関数を採用したとき\(J_p\)は
$$\begin{eqnarray}
J_p & = & \frac{1}{2}\sum_{j=1}^{N_L}(z_{jp}-t_{jp})^2\\
& = & \frac{1}{2}||\boldsymbol{z}^{(L)}_p-\boldsymbol{t}_p||^2
\end{eqnarray}$$
なので、勾配降下法の目的関数\(J\)は
$$\begin{eqnarray}
J &=& \sum_{p=1}^NJ_p \\
&=& \frac{1}{2}\sum_{p=1}^N\sum_j^{N_L}(z_{jp}-t_{jp})^2\\
&=&\frac{1}{2}\sum_{p=1}^N||\boldsymbol{z}^{(L)}_p-\boldsymbol{t}_p||^2
\end{eqnarray}$$
と表すことができます。以上を踏まえて出力層につながっている重みを更新する式を求めていきたいと思います。
誤差逆伝播法の考え方で説明した3ステップを思い出しましょう。
- (Step1):\(j\)番目に逆伝播されてくる誤差の合計値を計算
- (Step2):Step1の誤差の合計値は\(j\)番目のニューロンの出力時のスケールなので入力時のスケールに変換。
- (Step3):\(j\)番目のニューロンに入力された入力値の大きさに応じて平等に誤差を分配
でしたね。ここでは、まず、合成関数の微分を使ってStep1×Step2×Step3の形にします。
$$\begin{eqnarray}
\frac{\partial J_p(w^{(L)}_{ji})}{\partial w^{(L)}_{ji}}&=&\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{jp}}\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\frac{\partial u^{(L)}_{jp}}{\partial w^{(L)}_{ji}}
\end{eqnarray}$$
これが出たらほぼゴールです。あとは頑張って計算していくだけです。
$$\begin{eqnarray}
(Step1):\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{jp}} &=&\frac{\partial}{\partial z^{(L)}_{jp}}\left\{\frac{1}{2}\sum_j^{N_L}(z_{jp}-t_{jp})^2\right\}\\
&=&(z^{(L)}_{jp}-t_{jp})
\end{eqnarray}$$
$$\begin{eqnarray}
(Step2):\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}} &=&\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\\
&=&\frac{\partial}{\partial u^{(L)}_{jp}}f_L(u^{(L)}_{ji})\\
&=&f'_L(u^{(L)}_{ji})
\end{eqnarray}$$
$$\begin{eqnarray}
(Step3):\frac{\partial u^{(L)}_{jp}}{\partial w^{(L)}_{ji}} &=&\frac{\partial}{\partial w^{(L)}_{ji}}\left\{\sum_i^{N_{L-1}}w^{(L)}_{ji}z^{(L-1)}_{ip}\right\}\\
&=&z^{(L-1)}_{ip}
\end{eqnarray}$$
このようにして求めたものを元の式に戻してやると、
$$\begin{eqnarray}
\frac{\partial J_p(w^{(L)}_{ji})}{\partial w^{(L)}_{ji}}&=&\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{jp}}\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\frac{\partial u^{(L)}_{jp}}{\partial w^{(L)}_{ji}}\\
&=&(z^{(L)}_{jp}-t_{jp})f'_L(u^{(L)}_{ji})z^{(L-1)}_{ip}\\
&=&\epsilon^{(L)}_{jp}z^{(L-1)}_{ip}
\end{eqnarray}$$
となります。最後の式は、step1とstep2の部分(\(\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{jp}}\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\))を便宜上\(\epsilon^{(L)}_{jp}\)と置きました。
誤差逆伝播:中間層
出力層の部分ではStep1の微分の式は簡単でしたが、注目しているニューロンが中間層の場合、Step1の計算式が複雑になります。
つまり、注目してるニューロンが出力層であれば、step1の誤差は対応する教師信号だけからダイレクトに伝わってきましたが、中間層の場合、注目しているニューロンより後の層(出力層側)からの誤差を集約しなければなりません。この誤差の集約操作は、合成関数の微分における連鎖率(チェーンルール)で完全に実現可能です。
ですので、この章では連鎖率について紹介してから中間層の誤差逆伝播の式を導出していきたいと思います。
連鎖率(チェーンルール)
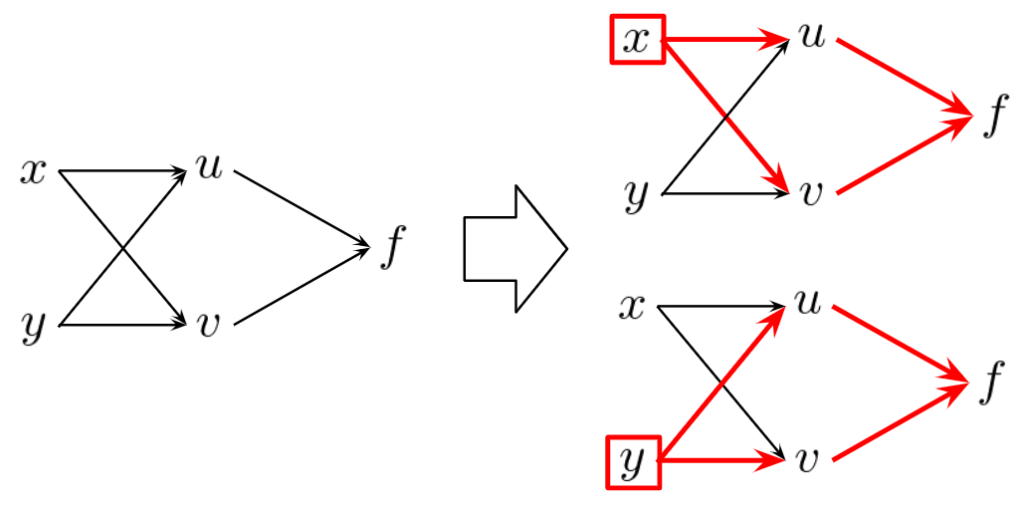
以下のような最も簡単な合成関数を考えてみます。
$$
f(u,v)\mbox{ ただし }u=u(x,y), v=v(x,y)
$$
この式を、ニューラルネットワークみたいにグラフィカルに表すと、以下の図の左のように表せます。このとき、\(x,y\)が\(f\)にどのように関与しているかを考えると、\(u\)を通るパスと\(v\)を通るパスの2つのパスから影響を与えていることが分かります。
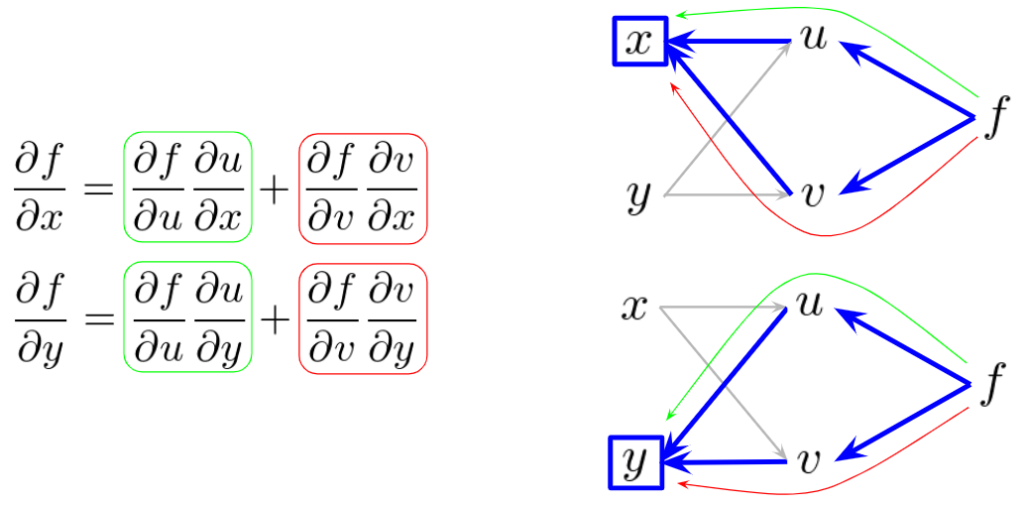
では、そのときの微分を考えてみます。これは、微積の授業で習ったようにそのままですね。\(x\)は\(u\)や\(v\)を介して\(f\)に関与していたので、微分のときも、\(u\)や\(v\)を介して考えていく必要があります。以下の偏微分の式において、第1項目が\(u\)のパスから、第2項目が\(v\)のパスからのものになります。これらを足し合わせたものが、\(x\)の偏微分値になります。
これは、まさに中間層の誤差逆伝播の式の導出の根幹をなすものになります。
中間層の誤差逆伝播の導出
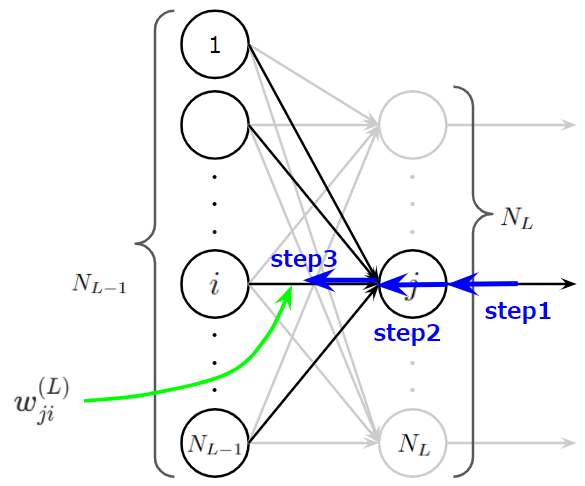
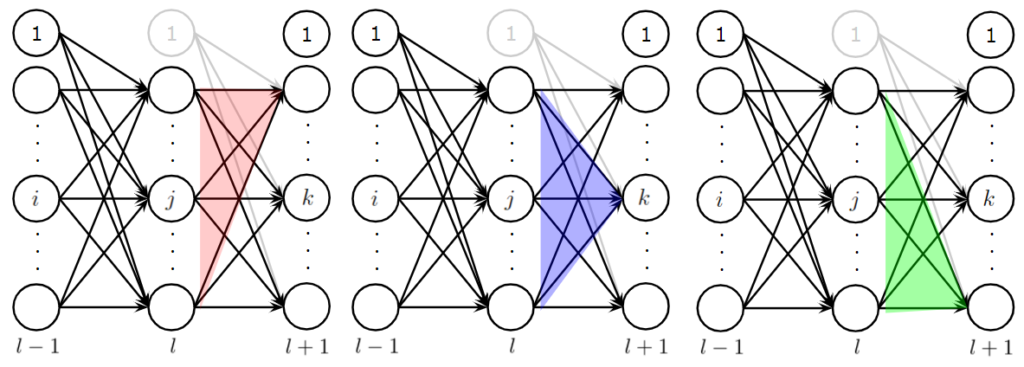
ここでは、\(l\)層目の中間層にある\(j\)番目のニューロンを考えたいと思います。ほかにも、図では便宜的に、\(l-1\)層目の\(i\)番目ニューロン、\(l+1\)層目の\(k\)番目ニューロンも与えています。
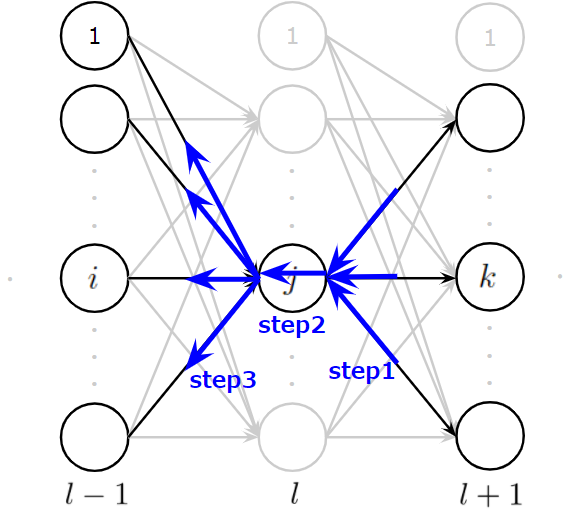
このとき、目的関数の微分値は、
$$\begin{eqnarray}
\frac{\partial J_p(w^{(l)}_{ji})}{\partial w^{(l)}_{ji}}&=&\frac{\partial J_p(w^{(l)}_{ji})}{\partial z^{(l)}_{jp}}\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}}\frac{\partial u^{(l)}_{jp}}{\partial w^{(l)}_{ji}}
\end{eqnarray}$$
出力層の時とほぼ同じで、指定している層が異なるだけです。Step2とStep3の部分の微分は出力層のときとほぼ同じです。異なるのはStep1の微分で、ここに連鎖率を適用して考えます。この際にちょっとしたテクニックがあり、目的関数の微分を1から全て求めようとしてはいけません。誤差逆伝播が可能な最小単位で考えて導出します。よって、\(l-1\)層と\(l\)層と\(l+1\)層の3層分を考え、\(l+1\)層が受け取る誤差は求まっているものとします。このとき、Step1は以下のように計算できます。
$$\begin{eqnarray}
(Step1):\frac{\partial J_p(w^{(l)}_{ji})}{\partial z^{(l)}_{jp}} &=&\sum_k^{N_{l+1}}\frac{\partial J_p(w^{(l)}_{ji})}{\partial u^{(l+1)}_{kp}}\frac{\partial u^{(l+1)}_{kp}}{\partial z^{(l)}_{jp}}\\
&=& \sum_k^{N_{l+1}}\frac{\partial J_p(w^{(l)}_{ji})}{\partial u^{(l+1)}_{kp}}w^{(l+1)}_{kj}\\
&=& \sum_k^{N_{l+1}}\epsilon^{(l+1)}_{kp}w^{(l+1)}_{kj}
\end{eqnarray}$$
$$\begin{eqnarray}
(Step2):\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}} &=&\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}}\\
&=&\frac{\partial}{\partial u^{(l)}_{jp}}f_l(u^{(l)}_{ji})\\
&=&f'_l(u^{(l)}_{ji})
\end{eqnarray}$$
$$\begin{eqnarray}
(Step3):\frac{\partial u^{(l)}_{jp}}{\partial w^{(l)}_{ji}} &=&\frac{\partial}{\partial w^{(l)}_{ji}}\left\{\sum_i^{N_{l-1}}w^{(l)}_{ji}z^{(l-1)}_{ip}\right\}\\
&=&z^{(l-1)}_{ip}
\end{eqnarray}$$
Step1の式では、出力層の更新式を導出した際にstep1とstep2の部分(\(\frac{\partial J_p(w^{(L)}_{ji})}{\partial^{(L)}_{jp}}\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\))を便宜上\(\epsilon^{(L)}_{jp}\)と置いたように、同様の微分操作であるstep1とstep2の部分(\(\frac{\partial J_p(w^{(l)}_{ji})}{\partial u^{(l+1)}_{kp}}\))を便宜上\(\epsilon^{(l+1)}_{kp}\)と置きました。
これより、
$$\begin{eqnarray}
\frac{\partial J_p(w^{(l)}_{ji})}{\partial w^{(l)}_{ji}}&=&\frac{\partial J_p(w^{(l)}_{ji})}{\partial z^{(l)}_{jp}}\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}}\frac{\partial u^{(l)}_{jp}}{\partial w^{(l)}_{ji}}\\
&=&\sum_k^{N_{l+1}}\epsilon^{(l+1)}_{kp}w^{(l+1)}_{kj}f'_l(u^{(l)}_{ji})z^{(l-1)}_{ip}\\
&=&\epsilon^{(l)}_{jp}z^{(l-1)}_{ip}
\end{eqnarray}$$
となります。最後の式は、\(\frac{\partial J_p(w^{(l)}_{ji})}{\partial z^{(l)}_{jp}}\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}}\)に対応する部分である\(\sum_k^{N_{l+1}}\epsilon^{(l+1)}_{kp}w^{(l+1)}_{kj}f'_l(u^{(l)}_{ji})\)を\(\epsilon^{(l)}_{jp}z^{(l-1)}_{ip}\)と置いています。
誤差逆伝播の導出:式の一般化
これで、出力層と中間層の誤差逆伝播の式が導出できたのですが、まだ覚えないと行けなさそうな見た目をしています。まだ一般化の余地があるので、両者の更新式をもっと一般化したいと思います。更新したいニューロンが出力層のときと中間層のときの更新式を再掲します。
$$\begin{eqnarray}
\mbox{出力層のとき:}\frac{\partial J_p(w^{(L)}_{ji})}{\partial w^{(L)}_{ji}}&=&\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{jp}}\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\frac{\partial u^{(L)}_{jp}}{\partial w^{(L)}_{ji}}\\
&=&(z^{(L)}_{jp}-t_{jp})f'_L(u^{(L)}_{ji})z^{(L-1)}_{ip}\\
&=&\epsilon^{(L)}_{jp}z^{(L-1)}_{ip}
\end{eqnarray}$$
$$\begin{eqnarray}
\mbox{中間層のとき:}\frac{\partial J_p(w^{(l)}_{ji})}{\partial w^{(l)}_{ji}}&=&\frac{\partial J_p(w^{(l)}_{ji})}{\partial z^{(l)}_{jp}}\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}}\frac{\partial u^{(l)}_{jp}}{\partial w^{(l)}_{ji}}\\
&=&\sum_k^{N_{l+1}}\epsilon^{(l+1)}_{kp}w^{(l+1)}_{kj}f'_l(u^{(l)}_{ji})z^{(l-1)}_{ip}\\
&=&\epsilon^{(l)}_{jp}z^{(l-1)}_{ip}
\end{eqnarray}$$
両式はよく似ていて、出力層の誤差逆伝播を更新式の誤差逆伝播の特別な場合としてとらえる表記をすることで、以下のように一般化できます。
$$\begin{eqnarray}
\frac{\partial J_p(w^{(l)}_{ji})}{\partial w^{(l)}_{ji}}&=&\frac{\partial J_p(w^{(l)}_{ji})}{\partial z^{(l)}_{jp}}\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}}\frac{\partial u^{(l)}_{jp}}{\partial w^{(l)}_{ji}}\\
&=&\epsilon^{(l)}_{jp}z^{(l-1)}_{ip}\\
\mbox{ただし }\epsilon^{(l)}_{jp}&=&\left\{\begin{array}{ll}
(z^{(l)}_{jp}-t_{jp})f'_l(u^{(l)}_{ji})&\mbox{\(l\)が出力層(\(l=L\))}\\
\sum_k^{N_{l+1}}\epsilon^{(l+1)}_{kp}w^{(l+1)}_{kj}f'_l(u^{(l)}_{ji})&\mbox{\(l\)が中間層(\(l<L\))}
\end{array}\right.
\end{eqnarray}$$
とかけます。これなら覚えられるかなって感じがしますよね。
誤差逆伝播の行列計算による実現
前のセクションでは誤差逆伝播の式を導出したわけですが、この定義通りにプログラムするのは泥臭く冗長で賢い計算方法ではありません。そのため、実用的に使用するには行列計算で実現すべきです。ですので、ここでは先ほど導いた式を行列計算の式に書き換えていきたいと思います。
まず、勾配降下法の行列バージョンは以下のようになります。
$$
\mbox{勾配降下法:}\boldsymbol{W}^{(l)}\leftarrow \boldsymbol{W}^{(l)}-\eta\nabla J(\boldsymbol{W}^{(l)})
$$
特に大きな変化はないですが、ここで行列計算により定式化したいのは\(-\eta\nabla J(\boldsymbol{W}^{(l)})\)です。
各パラメータの行列のサイズを定義する
何はともあれ、まずは最初に、各々のパラメータの行列サイズを定義しないと始まらないので、本記事では以下のように定義したいと思います。
- 出力層
- 重み行列 \(\boldsymbol{W}^{(L)}\) :\(N_L-bias×N_{L-1}\)
- 重み更新量 \(\Delta\boldsymbol{W}^{(L)}\):\(N_L-bias×N_{L-1}\)
- イプシロン \(\boldsymbol{\mathcal E}^{(L)}\) :\(N_L-bias×N\)
- 活性化関数適用前の値 \(\boldsymbol{U}^{(L)}\) :\(N_L-bias×N\)
- 層の出力 \(\boldsymbol{Z}_{ex}^{(L)}\) :\(N_L×N\)
- 中間層
- 重み行列 \(\boldsymbol{W}^{(l)}\) :\(N_l-bias×N_{l-1}\)
- 重み更新量 \(\Delta\boldsymbol{W}^{(l)}\):\(N_l-bias×N_{l-1}\)
- イプシロン \(\boldsymbol{\mathcal E}^{(l)}\) :\(N_l-bias×N\)
- 活性化関数適用前の値 \(\boldsymbol{U}^{(l)}\) :\(N_l-bias×N\)
- 層の出力 \(\boldsymbol{Z}_{ex}^{(l)}\) :\(N_l×N\)
\(N_l (1\leq l \leq L)\)は\(l\)層目のニューロン数、\(N\)はバッチサイズ、\(bias\)は全ての層にバイアスニューロンを設けるかを表すブール値で、設けないときに0(False)、設けるときに1(True)なる値を保持するものとします。また、\(\boldsymbol{Z}_{ex}\)はバイアスニューロンを追加した拡張表記とします。
※先ほどまでは、説明の便宜上\(N_l (1\leq l \leq L-1)\)はバイアスニューロンを含んだニューロン数で\(N_L\)はバイアスニューロンを含まない値としていましたが、以降ではプログラムの統一性、簡易性の上がる計算式で一般化するために、\(N_L\)もバイアスニューロンを含む値とします(もちろん、出力層のバイアスニューロンは使用しないので無視しますが)。
この行列サイズの定義方法に関して理論はないですね、ここはこう置きますってことにして誤差逆伝播の式を構築していくだけです。
更新量\(-\eta\nabla J(\boldsymbol{W}^{(l)})\)と\(\boldsymbol{\mathcal E}^{(l)}\)の行列計算による実現
いま、\(\Delta\boldsymbol{W}^{(l)}\)は\(-\eta\nabla J(\boldsymbol{W}^{(l)})\)を表しています。上で用意した文字を使うと、出力層の\(\Delta\boldsymbol{W}^{(L)}\)と中間層の\(\Delta\boldsymbol{W}^{(l)}\)は
$$\begin{eqnarray}
\underset{(N_L-bias×N_{L-1})}{\underline{\Delta\boldsymbol{W}^{(L)}}}&=&\underset{(N_L-bias×N)(N×N_{L-1})}{\underline{-\eta \frac{1}{N}\boldsymbol{\mathcal E}^{(L)}(\boldsymbol{Z}_{ex}^{(L-1)})^T}}\\
\underset{(N_l-bias×N_{l-1})}{\underline{\Delta\boldsymbol{W}^{(l)}}}&=&\underset{(N_l-bias×N)(N×N_{l-1})}{\underline{-\eta \frac{1}{N}\boldsymbol{\mathcal E}^{(l)}(\boldsymbol{Z}_{ex}^{(l-1)})^T}}\\
\end{eqnarray}$$
と表せます。アンダーラン下に行列の形状を示したので、確認してみてください。このようにして求まる\(\Delta\boldsymbol{W}^{(l)}\)で、
$$
\boldsymbol{W}^{(l)}\leftarrow \boldsymbol{W}^{(l)}+\Delta\boldsymbol{W}^{(l)}
$$
のように更新するわけですので、\(\boldsymbol{\mathcal E}^{(l)}\)をしっかりと行列計算で求める必要があります。前の章で求めたように、
$$
\epsilon^{(l)}_{jp}=\left\{\begin{array}{ll}
(z^{(l)}_{jp}-t_{jp})f'_l(u^{(l)}_{ji})&\mbox{\(l\)が出力層(\(l=L\))}\\
\sum_k^{N_{l+1}}\epsilon^{(l+1)}_{kp}w^{(l+1)}_{kj}f'_l(u^{(l)}_{ji})&\mbox{\(l\)が中間層(\(l<L\))}
\end{array}\right.
$$
を思い出しましょう。
出力層:\(\boldsymbol{\mathcal E}^{(L)}\)
天下り的になりますが、出力層のイプシロン\(\boldsymbol{\mathcal E}^{(L)}\)は
$$
\underset{(N_L-bias×N)}{\underline{\boldsymbol{\mathcal E}^{(L)}}} = \underset{((N_L-bias×N)-(N_L-bias×N))\odot (N_L-bias×N)}{\underline{(\boldsymbol{Z}_{ex}^{(L)}[bias:] - \boldsymbol{T})\odot f'_L(\boldsymbol{U}^{(L)})}}
$$
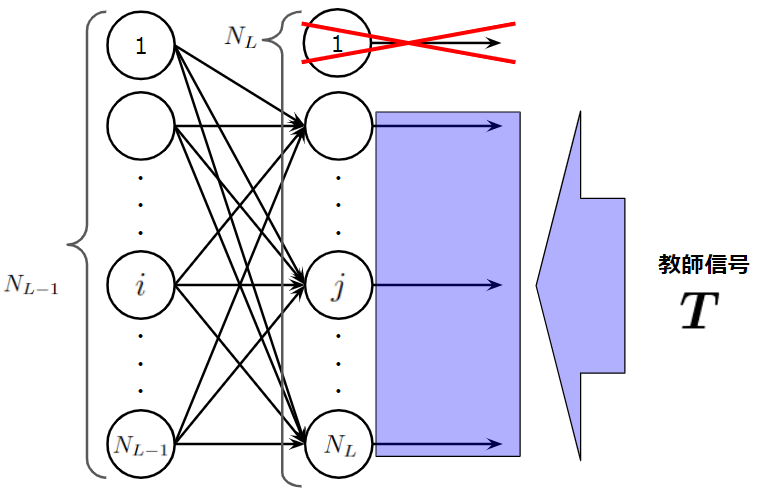
となります。注意してほしいのは、\(\boldsymbol{Z}_{ex}^{(L)}[bias:]\)の部分で、出力層のバイアスニューロンは他の層にバイアスニューロンがあるように、すべての層の構造に統一性を持たせ、誤差逆伝播を実行する関数を単純にするために用意したものであり実質無駄、つまり全く役に立たない要らないニューロンです。そのため、NumPyのスライスを使用して\(bias\)がTrueなら1行目を取り除いたもの([1:])を、Falseなら何も取り除かずにそのままのもの([0:])を利用することを表しています。以下に、bias=Trueのときの任意の層\(l\)の出力行列を示します。1列目(青枠で囲われた部分)は\(l\)層目のバイアスニューロンの出力なので全て1です。これを参考に考えてみると、出力層のバイアスニューロンを考慮せずに誤差を求めるには、\(\boldsymbol{Z}_{ex}^{(L)}[bias:]\)とすればいいことが分かると思います。

中間層:\(\boldsymbol{\mathcal E}^{(l)}\)
次に、中間層のイプシロンの式を以下に示します。
$$
\underset{(N_l-bias×N)}{\underline{\boldsymbol{\mathcal E}^{(l)}}} = \underset{(N_l-bias×N_{l+1}-bias)(N_{l+1}-bias×N)\odot (N_l-bias×N)}{\underline{(\boldsymbol{W}^{(l+1)}[:, bias:])^T\boldsymbol{\mathcal E}^{(l+1)}\odot f'_l(\boldsymbol{U}^{(l)})}}
$$
として求めることができます。ここで注意が必要なのは、\(\boldsymbol{W}^{(l+1)}[:, bias:]\)の[:, bias:]です。\(\boldsymbol{W}^{(l+1)}\)行列は、行数が\(l+1\)層目ニューロン数から必要に応じてバイアスニューロンを除いたもので、列数は、\(\)層目のニューロン数です。今求めたい\(\boldsymbol{\mathcal E}^{(l)}\)は\(\boldsymbol{W}^{(l)}\)行列の更新量であり、そのためには、適宜バイアスニューロンを除いた\(l\)層目の全ニューロンが受け取るイプシロン\(\boldsymbol{\mathcal E}^{(l)}\)を後の層のイプシロン\(\boldsymbol{\mathcal E}^{(l+1)}\)から求める必要がありますが、\(l-1\)層目と結合をもたない\(l\)層目のバイアスニューロンが受け取るイプシロンを求める必要はないため、\(\boldsymbol{W}^{(l+1)}[:, bias:]\)を使用しています。先ほどと同様、以下にbias=Trueのとき任意の\(l\)における\(\boldsymbol{W}^{(l)}\)行列を示します。最も左に位置する列ベクトル(青で囲った部分)は\(l\)層目の各ニューロンのバイアスですので、\(\boldsymbol{W}^{(l+1)}[:, bias:]\)の[:, bias:]はNumPyを使って青の部分を省く操作になります。

発展:交差エントロピー誤差関数を使用したときの誤差逆伝播
さきほどは二乗誤差関数を損失関数と仮定して、活性化関数を指定せず導出をしてきました。機械学習には回帰問題と分類問題という2つの大きな課題があり、二乗誤差関数は回帰問題で頻繁に使用されるものです。では、分類問題、とくに他クラス分類問題で頻繁に使用される交差エントロピー誤差関数を使用したときの誤差逆伝播の式はどのようになるのでしょうか。交差エントロピー誤差関数を使用するときは、出力層の活性化関数にソフトマックス関数を使用するので、出力層の誤差逆伝播について、ソフトマックス関数を改定して、導出していきたいと思います。その前に、ソフトマックス関数について及びその導関数について解説します。その後に、誤差逆伝播の式を導出します。そして、最後に、行列による計算方法を示したいと思います。
交差エントロピー
交差エントロピーの説明は後の記事で少し触れるので、詳しい説明は避けますが、以下のような式で書かれます。
$$
J=-\sum_{p=1}^N\sum_{j=1}^{N_L}t_{jp}\log z^{(L)}_{jp}
$$
この式はバッチ処理を前提とした式です。ここで、バッチデータの中の\(p\)番目のデータに関する交差エントロピーは、
$$
J_p = -\sum_{j=1}^{N_L}t_{jp}\log z^{(L)}_{jp}
$$
です。以降では、\(J_p\)をベースに考えていきたいと思います。
ソフトマックス関数とは
出力層に複数のニューロンがあるとき、出力層に使用している活性化関数がシグモイド関数だと、個々のニューロンが独立してそれぞれに属する確率を出力します。これだと多くのクラスから1つのクラスを予測するような多クラス分類問題では嬉しくないので、出力された値を全ての考慮したうえで適切な確率に変換する必要があります。その際にソフトマックス関数が使用されます。
$$
softmax(x_i)=\frac{e^{x_i}}{\sum_k e^{x_k}}
$$
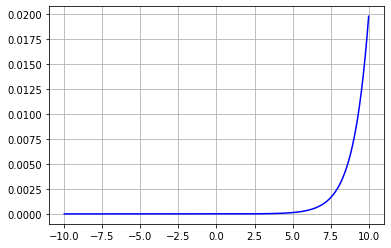
このグラフは値が大きくなると、急激に確率が増すことを示しています。イメージしやすくかみ砕いて説明すると、小さい値はもっと小さく、大きい値はもっと大きく見えるように変換することができます。以下の図を見れば一目瞭然です。図にはソフトマックス適用前の出力層の線形ユニットからの出力を表すグラフ(上)とソフトマックス適用後の出力のグラフ(上)が描かれています。
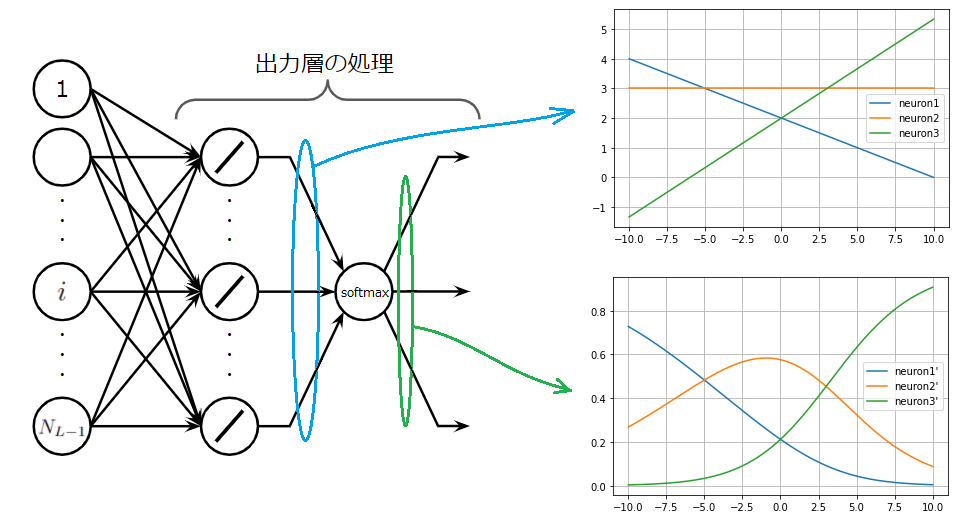
上のグラフにおいて、横軸が10のときの3つのニューロンの出力を見ると、neuron1,neuron2,neuron3は順番に0, 3, 5.3程度の値となっています。この値はソフトマックス関数により、下のグラフの横軸が10のときの値に写像されまっす。ソフトマックス関数を適用した後のニューロンを、neuron1',neuron2',neuron3'とすると、値は順番に、0, 0.1, 0.92程度になています。上のグラフでは、neuron2とneuron3の値は、あまり離れていなかったのに、ソフトマックス関数により、大きく引き離されていることが分かります。ソフトマックス関数はこのような特性を持ちます。
ソフトマックス関数の導関数
誤差逆伝播を計算するには、今まで見てきたように活性化関数の導関数が必要です。ソフトマックス関数の導関数の導出は簡単なので省略しますが、以下のように表すことができます。自分自身の値を使って導関数が表せるというのは、シグモイド関数と同じです。
$$
\frac{d}{d x_j}softmax(x_i)=\left\{\begin{array}{ll}
softmax(x_i)(1-softmax(x_j))&i=j\\
-softmax(x_i)softmax(x_j)&i\neq j
\end{array}\right.$$
これは、\(i=j\)のときは1でそれ以外は0になる関数\(\delta_{ij}\)を用意することで、
$$
\frac{d}{d x_j}softmax(x_i)=softmax(x_i)(\delta_{ij}-softmax(x_j))\\
$$
のように簡単に表すことができます。これがソフトマックス関数の導関数です。
ソフトマックス関数使用時の誤差逆伝播のイメージ
それでは、出力層の誤差であるイプシロン\(\epsilon^{(L)}_{jp}\)を導出したいと思います。中間層については、上位の誤差を再帰的に利用することで求められるので省略します。まず、ここで注意点があります。ソフトマックス関数を適用した層は、シグモイド関数を適用した出力層とは異なる形になります。具体的には以下の図を見てください。
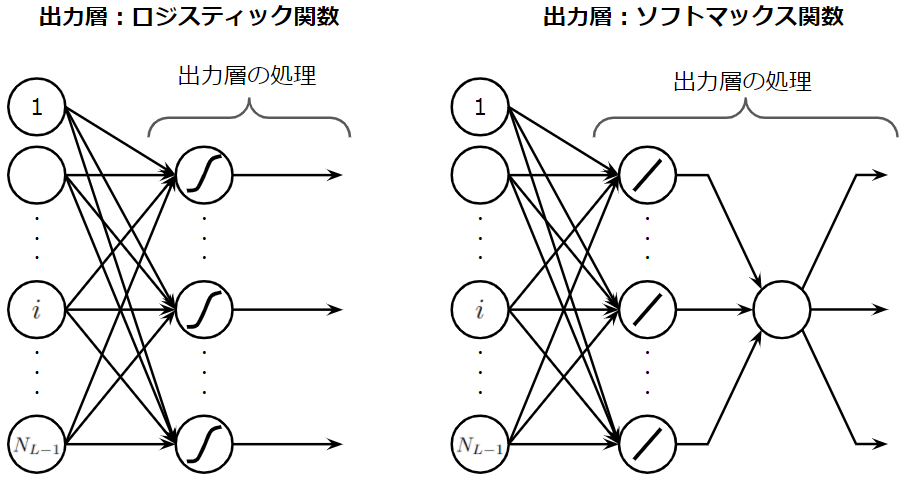
図からは、ソフトマックス関数による計算操作により、出力層に属する全てのニューロンが一旦集約されていることが分かると思います。そのため、誤差逆伝播計算は以下の図で示すようなプロセスで行われる必要があります。
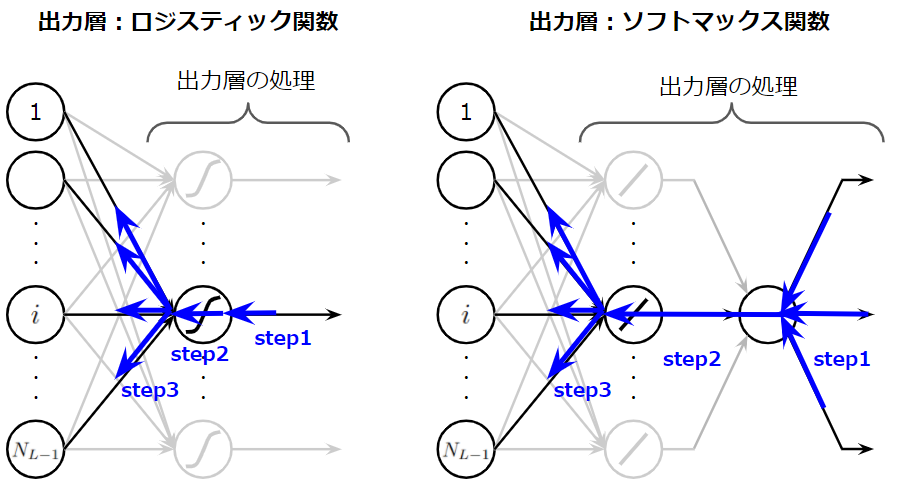
ですので、結構上の方で説明した、中間層の誤差逆伝播の式、つまり、チェーンルールを適用していく必要があります。
誤差逆伝播の式の導出
これから求めたいのは、出力層の誤差ですが、上記の理由からチェーンルールを適用した中間層と同じ式を使用する必要があることが分かったと思います。そして、チェーンルールはStep1で適用されることを思い出しましょう。では、勾配を求める式を変換していきます。
$$\begin{eqnarray}
\frac{\partial J_p(w^{(L)}_{ji})}{\partial w^{(L)}_{ji}}&=&\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{jp}}\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\frac{\partial u^{(L)}_{jp}}{\partial w^{(L)}_{ji}}\\
&=&\left\{\sum_k^{N_{L+1}}\frac{\partial J_p(w^{(L)}_{ji})}{\partial u^{(L+1)}_{kp}}\frac{\partial u^{(L+1)}_{kp}}{\partial z^{(L)}_{jp}}\right\}
\left\{\frac{\partial z^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\right\}
\left\{\frac{\partial u^{(L)}_{jp}}{\partial w^{(L)}_{ji}}\right\}
\end{eqnarray}$$
ただし、これは中間層の式をそのまま出力層に適用したものですので注意が必要です。具体的には存在しないパラメータ\(u^{(L+1)}_{kp}\)があるので、これは出力層の出力\(z^{(L)}_{kp}\)に対応し、また、恒等関数をもつ出力層のソフトマックス適用前のニューロンの値は\(z^{(L)}_{jp}\)ではなく、\(u^{(L)}_{jp}\)です。また、\(N_{L+1}\)は\(N_L\)と同じです。以下の図を見てパラメータの対応関係を確認してください。
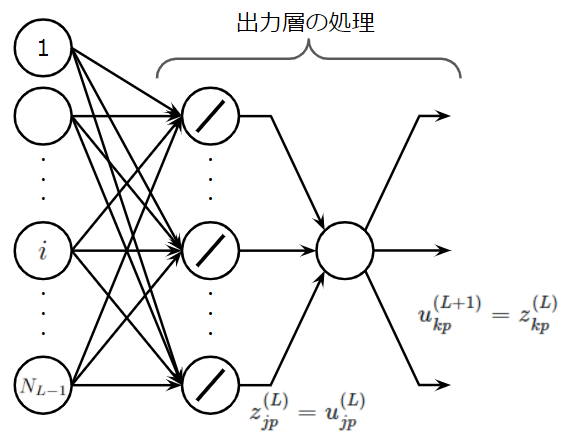
このとき、先ほどの式は、
$$\begin{eqnarray}
\frac{\partial J_p(w^{(L)}_{ji})}{\partial w^{(L)}_{ji}}&=&\left\{\sum_k^{N_{L}}\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{kp}}\frac{\partial z^{(L)}_{kp}}{\partial u^{(L)}_{jp}}\right\}
\left\{\frac{\partial u^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\right\}
\left\{\frac{\partial u^{(L)}_{jp}}{\partial w^{(L)}_{ji}}\right\}
\end{eqnarray}$$
と書き換えられます。これをそのまま計算すると、
$$\begin{eqnarray}
\frac{\partial J_p(w^{(L)}_{ji})}{\partial w^{(L)}_{ji}}&=&\left\{\sum_k^{N_{L}}\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{kp}}\frac{\partial z^{(L)}_{kp}}{\partial u^{(L)}_{jp}}\right\}
\left\{\frac{\partial u^{(L)}_{jp}}{\partial u^{(L)}_{jp}}\right\}
\left\{\frac{\partial u^{(L)}_{jp}}{\partial w^{(L)}_{ji}}\right\}\\
&=&\left\{\sum_k^{N_{L}}\frac{\partial J_p(w^{(L)}_{ji})}{\partial z^{(L)}_{kp}}\frac{\partial z^{(L)}_{kp}}{\partial u^{(L)}_{jp}}\right\}z^{(L-1)}_{ip}\\
&=&\left\{\sum_k^{N_{L}}\frac{\partial}{\partial z^{(L)}_{kp}}\left[-\sum_{j=1}^{N_L}t_{jp}\log z^{(L)}_{jp}\right]\frac{\partial z^{(L)}_{kp}}{\partial u^{(L)}_{jp}}\right\}z^{(L-1)}_{ip}\\
&=&-\sum_k^{N_{L}}\frac{t_{kp}}{z^{(L)}_{kp}}z^{(L)}_{kp}(\delta_{kj}-z^{(L)}_{jp})z^{(L-1)}_{ip}\\
&=&-\sum_k^{N_{L}}t_{kp}(\delta_{kj}-z^{(L)}_{jp})z^{(L-1)}_{ip}\\
&=&-\left\{\sum_k^{N_{L}}t_{kp}\delta_{kj}-z^{(L)}_{jp}\sum_k^{N_{L}}t_{kp}\right\}z^{(L-1)}_{ip}\\
&=&-(t_{jp}-z^{(L)}_{jp})z^{(L-1)}_{ip}\\
&=&(z^{(L)}_{jp}-t_{jp})z^{(L-1)}_{ip}\\
\end{eqnarray}$$
結果はとても簡単になります。これより、
$$\begin{eqnarray}
\frac{\partial J_p(w^{(l)}_{ji})}{\partial w^{(l)}_{ji}}&=&\frac{\partial J_p(w^{(l)}_{ji})}{\partial z^{(l)}_{jp}}\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}}\frac{\partial u^{(l)}_{jp}}{\partial w^{(l)}_{ji}}\\
&=&\epsilon^{(l)}_{jp}z^{(l-1)}_{ip}\\
\mbox{ただし }\epsilon^{(l)}_{jp}&=&\left\{\begin{array}{ll}
(z^{(l)}_{jp}-t_{jp})&\mbox{\(l\)が出力層(\(l=L\))}\\
\sum_k^{N_{l+1}}\epsilon^{(l+1)}_{kp}w^{(l+1)}_{kj}f'_l(u^{(l)}_{ji})&\mbox{\(l\)が中間層(\(l<L\))}
\end{array}\right.
\end{eqnarray}$$
行列計算による実現
先ほどの結果を見れば、行列による計算式は、一目瞭然でして、以下のようになります。
$$\begin{eqnarray}
\Delta\boldsymbol{W}^{(l)}&=&-\eta \frac{1}{N}\boldsymbol{\mathcal E}^{(l)}(\boldsymbol{Z}_{ex}^{(l-1)})^T\\
\mbox{ただし }\boldsymbol{\mathcal E}^{(l)}&=&\left\{\begin{array}{ll}
(\boldsymbol{Z}_{ex}^{(l)}[bias:] - \boldsymbol{T})&\mbox{\(l\)が出力層(\(l=L\))}\\
(\boldsymbol{W}^{(l+1)}[:, bias:])^T\boldsymbol{\mathcal E}^{(l+1)}\odot f'_l(\boldsymbol{U}^{(l)})&\mbox{\(l\)が中間層(\(l<L\))}
\end{array}\right.
\end{eqnarray}$$
まとめ
ここでは、長ったらしい難しい式変形は省略し、要点を掴みつつ結論をまとめます。
まず、勾配降下法は、最適解を近似的に求める勾配法の1つで、
$$
w\leftarrow w-\eta\nabla J(w)
$$
と表されました。しかし、この勾配を求めるのはとても大変ですので何とかして効率的に求めたいものです。そこで使用されるのが誤差逆伝播法です。本記事では誤差逆伝播法を3つのステップ、
- (Step1):\(j\)番目に逆伝播されてくる誤差の合計値を計算
- (Step2):Step1の誤差の合計値は\(j\)番目のニューロンの出力時のスケールなので入力時のスケールに変換。
- (Step3):\(j\)番目のニューロンに入力された入力値の大きさに応じて平等に誤差を分配
に分けえて考え、実際の微分でも3ステップに分割して考えられることを説明しました。
それぞれについて場合分けしながら導出し、式を一般化することで誤差逆伝播法は以下のような式で表せることを紹介しました。
$$\begin{eqnarray}
\frac{\partial J_p(w^{(l)}_{ji})}{\partial w^{(l)}_{ji}}&=&\frac{\partial J_p(w^{(l)}_{ji})}{\partial z^{(l)}_{jp}}\frac{\partial z^{(l)}_{jp}}{\partial u^{(l)}_{jp}}\frac{\partial u^{(l)}_{jp}}{\partial w^{(l)}_{ji}}\\
&=&\epsilon^{(l)}_{jp}z^{(l-1)}_{ip}\\
\mbox{ただし }\epsilon^{(l)}_{jp}&=&\left\{\begin{array}{ll}
(z^{(l)}_{jp}-t_{jp})f'_l(u^{(l)}_{ji})&\mbox{\(l\)が出力層(\(l=L\))}\\
\sum_k^{N_{l+1}}\epsilon^{(l+1)}_{kp}w^{(l+1)}_{kj}f'_l(u^{(l)}_{ji})&\mbox{\(l\)が中間層(\(l<L\))}
\end{array}\right.
\end{eqnarray}$$
しかし、このままでは、プログラムで実行するのに賢いやり方ではないので、行列計算の式に書き換えていきました。その結果、勾配降下法
$$
\boldsymbol{W}^{(l)}\leftarrow \boldsymbol{W}^{(l)}-\eta\nabla J(\boldsymbol{W}^{(l)})
$$
の勾配\(-\eta\nabla J(\boldsymbol{W}^{(l)})(=\Delta\boldsymbol{W}^{(l)})\)は、出力層側から順に伝わってくる\(\boldsymbol{\mathcal E}^{(l)}\)を使って、
$$\begin{eqnarray}
\Delta\boldsymbol{W}^{(l)}&=&-\eta \frac{1}{N}\boldsymbol{\mathcal E}^{(l)}(\boldsymbol{Z}_{ex}^{(l-1)})^T\\
\mbox{ただし }\boldsymbol{\mathcal E}^{(l)}&=&\left\{\begin{array}{ll}
(\boldsymbol{Z}_{ex}^{(l)}[bias:] - \boldsymbol{T})\odot f'_l(\boldsymbol{U}^{(l)})&\mbox{\(l\)が出力層(\(l=L\))}\\
(\boldsymbol{W}^{(l+1)}[:, bias:])^T\boldsymbol{\mathcal E}^{(l+1)}\odot f'_l(\boldsymbol{U}^{(l)})&\mbox{\(l\)が中間層(\(l<L\))}
\end{array}\right.
\end{eqnarray}$$
のように表すことができました。
結構長い記事になりましたが、最後までお読みいただきありがとうございました。明日は、誤差逆伝播で活性化関数の微分が行われる際の操作について様々な活性化関数の例を挙げながら説明していきたいと思います。
