本記事では分散共分散行列について学びたいと思います。
期待値・分散・共分散を定義する
まず2つの離散型確率変数を以下のように定義します。
\(x \in \{x_1, x_2, \cdots, x_n\}\), 生起確率を\(P_x(x_i)\)ただし\( (1 \leq i \leq n) \)
\(y \in \{y_1, y_2, \cdots, y_m\}\), 生起確率を\(P_y(y_j)\)ただし\( (1 \leq j \leq m) \)
このとき、\(x\)の期待値は定義より
\(E[x] = \sum_ix_iP_x(x_i)\)
と表されます。期待値は平均値を表しますが、出現しうる値\(x_i\)についての平均ではなく、それぞれに重みとして確率を掛け合わせたもの、つまり無限回の試行したときに期待される値です。つまり、\(x \in \{1, 10\}, P_x[x=1] = 0.8, P_x[x=10] = 0.2\)のとき、期待値(無限回の試行による出現した値の平均値)は5.5ではなく、\(1 × 0.8 + 10 × 0.2 = 2.8\)となります。
次に分散\(V[x]\)を定義します。分散は偏差\(x - E[x]\)を二乗したものの期待値を表し、式は以下のようになります。
\(\begin{eqnarray}
V[x] &=& E[(x - E[x])^2] \\
&=& E[x^2] - (E[x])^2\\
\end{eqnarray}\)
上の式変形の補足として途中式を示すと、
\(\begin{eqnarray}
V[x] &=& E[(x - E[x])^2] \\
&=& E[x^2 - 2xE[x] + (E[x])^2]\\
&=& \sum_i(x_i^2 - 2x_iE[x] + (E[x])^2)P_x(x_i)\\
&=& \sum_ix_i^2 P_x(x_i) - \sum_i 2x_iE[x] P_x(x_i) + \sum_i (E[x])^2P_x(x_i)\\
&=& E[x^2] - 2E[x]E[x] + (E[x])^2 \\
&=& E[x^2] - (E[x])^2
\end{eqnarray}\)
となります。3行目と4行目については意識しなくても問題ありません。
共分散\(s_{xy}\)の説明に入る前に、上で定義した分散を\(s_{xx}\)という表記で統一させることにします。
\(s_{xx} = V[x] = E[(x - E[x])(x - E[x])]\)
共分散\(s_{xy}\)は、以下の式で定義します。
\(s_{xy} = E[(x - E[x])(y - E[y])]\)
分散が理解できれば、共分散は難しかりません。分散を拡張したものを共分散と考えることができますが、逆の見方として、共分散の特別な場合が分散と考えれば理解しやすいです。
分散の解釈
説明の便宜上、以下では連続確率分布によって生起された乱数を使用して説明させていただきます。このセクションはイメージ重視なので、正確性に欠けている点はご了承ください。
以下の図にプロットされた点は、平均5で分散2の正規分布に従って生成されたランダム値です。


ここで、\(x - E[x]\)に対応する操作、平均までの距離(赤矢印)だけ各々から引き、平均を0にします。

次に、\( (x - E[x])^2\)に対応する操作(全て二乗)し、期待値を求めます。全ての値を二乗するので、分散は必ず正になります。
共分散の解釈
二次元座標上に、二つの確率変数\(x, y\)が図のように分布しているとします。図では横軸は\(x\)、縦軸は\(y\)で、\(x, y\)の両者とも期待値は5です。

このとき、それぞれの期待値を引いたときの、\(x - E[x]\)と\(y - E[y]\)の分布は以下のようになります。
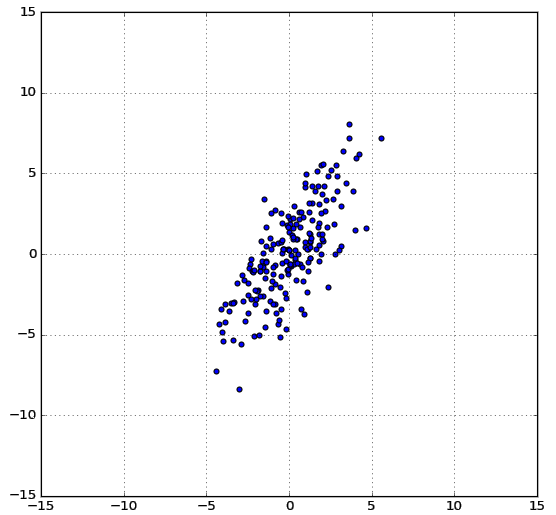
次に、両者を掛け合わせ、期待値を計算することで、共分散が求まります。
※共分散では\( (x - E[x])(y - E[y])\)が必ず正とは限らないことに起因して、値は負にもなり得ます。
共分散の正負により、両データの傾向を読み取ることができます。
・共分散が正:\( (x - E[x])\)が正の時は\( (y - E[y])\)が正、\( (x - E[x])\)が負の時は\( (y - E[y])\)が負となる傾向がある。
・共分散が負:\( (x - E[x])\)が正の時は\( (y - E[y])\)が負、\( (x - E[x])\)が負の時は\( (y - E[y])\)が正となる傾向がある。
この値を-1から1の間に正規化することで、より分かりやすくしたものが、相関係数です。相関係数は以下の式
\(相関係数 = \frac{xとyの共分散}{(xの標準偏差) × (yの標準偏差)}\)
で求められ、\(相関係数 \propto 共分散\) という関係があることが分かります。
分散共分散行列
先ほど、共分散の特別な場合が分散と考えれば理解しやすいと説明したように、 \(x\)と\(x\)の共分散(これは\(x\)の分散)を\(s_{xx}\)、\(x\)と\(y\)の共分散を\(s_{xy}\) 、\(y\)と\(x\)の共分散を\(s_{yx}\) 、\(y\)と\(y\)の共分散(これは\(y\)の分散)を\(s_{yy}\)として考え、これを行列にします。
\( \sum = \begin{pmatrix}
s_{xx}&s_{xy}\\
s_{yx}&s_{yy}\\
\end{pmatrix}\)
これが分散共分散行列で、\(\sum\)で表します。分散共分散の式の定義は以下の式で表されます。
\(\sum = E\left [\left\{\begin{pmatrix}x\\y\end{pmatrix} - E \begin{pmatrix}x\\y\end{pmatrix} \right\} \left\{\begin{pmatrix}x\\y\end{pmatrix} - E \begin{pmatrix}x\\y\end{pmatrix} \right\} ^T\right ]\)
追加
以下では、共分散(covariance)を\(Cov[x, y]\)で表すこととします。共分散を導入すると次のような式が成立します。
\(V[x + y] = V[x] + V[y] + 2Cov[x, y]\)
(証明)
\( V[x] = E[x^2] - (E[x])^2 を使用すると \)
\(\begin{eqnarray}
V[x + y] &=& E[(x + y)^2] - (E[x + y])^2\\
&=& E[x^2 + 2xy + y^2] - (E[x] + E[y])^2\\
&=& E[x^2] + 2E[xy] + E[y^2] - (E[x])^2 - 2E[x]E[y] - (E[y])^2\\
\end{eqnarray}\)
なので、
\(\begin{eqnarray}
V[x + y] - V[x] - V[y] &=& E[x^2] + 2E[xy] + E[y^2] - (E[x])^2 - 2E[x]E[y] - (E[y])^2 - E[x^2] + (E[x])^2 - E[y^2] + (E[y])^2\\
&=& 2(E[xy] - E[x]E[y])
\end{eqnarray}\)
また、
\(\begin{eqnarray}
Cov[x, y] &=& E[(x - E[x])(y - E[y])]\\
&=& E[xy - xE[y] - yE[x] + E[x]E[y]]\\
&=& E[xy] - E[x]E[y] - E[x]E[y] + E[x]E[y]\\
&=& E[xy] - E[x]E[y]
\end{eqnarray}\)
よって
\(V[x + y] = V[x] + V[y] + 2Cov[x, y]\)
が成立する。
この式は、分散共分散行列\(\sum\)を使用して以下のように表すことができます。
\(\begin{eqnarray}V[x + y] &=& V[x] + V[y] + 2Cov[x, y]\\ &=&
\begin{pmatrix}
1&1
\end{pmatrix}
\begin{pmatrix}
V[x]&Cov[x, y]\\
Cov[y, x]&V[y]
\end{pmatrix}
\begin{pmatrix}
1\\
1
\end{pmatrix}\\ &=& \begin{pmatrix}
1&1
\end{pmatrix} \sum \begin{pmatrix}
1\\
1
\end{pmatrix} \end{eqnarray}\)
