RRTの欠点を改善したRRT*とは

RRT

RRT（Rapidly-exploring Random Tree）とは、3次元空間など割と高次元空間における経路生成や軌道生成を、ランダムにノードを増やしていくことで実現する探索手法です。平面においては、ダイクストラ、その改良のA*がありますが、RRTは3次元空間で使えるダイクストラ的な、後で説明するRRT*はA*的な位置付けだと理解していただければ初めの理解としては十分でしょう。

RRTについては以下の記事で詳しく解説しているので、興味がありましたら、読んでみてください。

: Rapidly-exploring Random Tree：RRTとは
本記事では、ロボットのアームの制御などでも使用されるRRT（Rapidly-exploring Random Tree）について、概要とアルゴリズム、そして実際にプログラムコードを動することろまで解説 ...

ここでは、以前の記事でせつめいしたRRTのアルゴリズムについて簡単に説明します。RRTのアルゴリズムは以下のようになっています。

処理(1)：グラフ\(G=(V, E)=(\{x_{init}\}, \emptyset)\)で初期化
処理(2)：\(n\)回反復処理
- 処理(2-1)：探索空間内の1点\(x_{rand}\)をサンプリング
- 処理(2-2)：\(x_{rand}\)に最も近いグラフ\(G\)上の点(\(x_{nearest}\in V\))を計算
- 処理(2-3)：\(x_{nearest}\)から\(x_{rand}\)を結んだ線上の\(x_{nearest}\)から指定の距離のところを表す点\(x_{new}\)を計算
- 処理(2-4)：\(x_{new}\)がグラフ\(G\)のノード\(V\)に存在せず、かつ、\(x_{new}\)と\(x_{nearest}\)の間に障害物がないことをチェック
処理(3)：ゴールに辿り着いたか確認
処理(4)：\(x_{init}\)から\(x_{goal}\)までのパスを計算

この手順を分かりやすく図で示したのが以下になります。

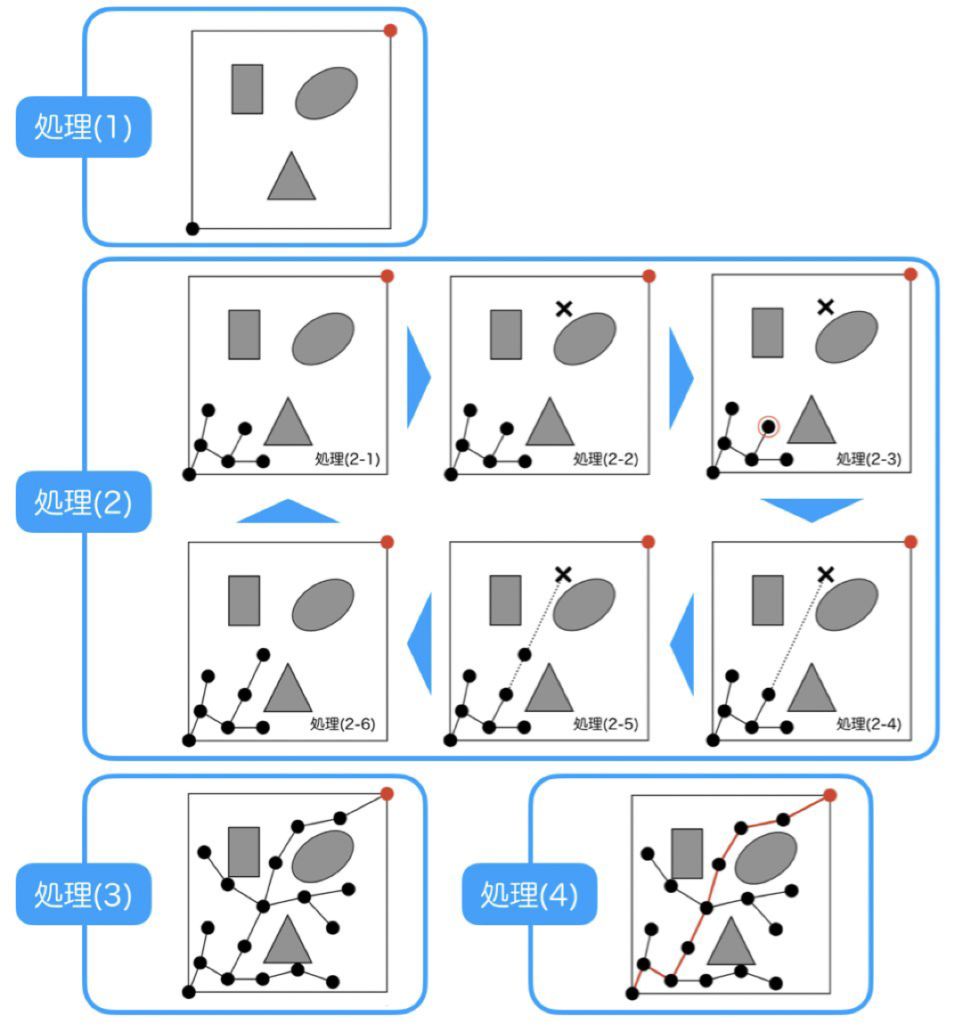
処理(1)でグラフを初期化、処理(2)でランダムサンプリングを使って木を大きく、処理(3)でゴールへの到達確認、処理(4)でゴールに到達していた場合はパスを返す、という感じになります。

RRT*

RRTの利点は、とても単純なアルゴリズムであるにも関わらず、高次元の探索空間における経路生成や軌道生成が可能なところで、ロボットアームの制御などで使用されます。一方で、RRTの欠点として、得られたパスの最適性は全く保証されない点です。そのため、遠回りしたり、ギザギザした無駄の多いパスを生成することは十分にあり得ます。そこで、ある程度の最適性が欲しいということで考えられたのが、RRT*（RRTスター）です。

RRT*は以下の論文で発表されました。

https://arxiv.org/abs/1005.0416

RRT*アルゴリズム

RRT*のアルゴリズムを以下に示します。これは、論文に記載されているアルゴリズムを簡略化して記載しています。

処理(1)：グラフ\(G=(V, E)=(\{x_{init}\}, \emptyset)\)で初期化
処理(2)：\(n\)回反復処理
- 処理(2-1)：探索空間内の1点\(x_{rand}\)をサンプリング
- 処理(2-2)：\(x_{rand}\)に最も近いグラフ\(G\)上の点(\(x_{nearest}\in V\))を計算
- 処理(2-3)：\(x_{nearest}\)から\(x_{rand}\)を結んだ線上の\(x_{nearest}\)から指定の距離のところを表す点\(x_{new}\)を計算
- 処理(2-4)：\(x_{nearest}\)と\(x_{new}\)を結ぶ線が障害物と交差していなければ以下を実行
  - 処理(2-4-1)：\(x_{new}\)の近傍にあるグラフの複数のノードを対象に、\(x_{init}\)から\(x_{new}\)に最小のコスト（最短）で到達できるノード\(x_{min}\)を特定
  - 処理(2-4-2)：\(V \leftarrow V \cup \{x_{new}\}\)、\(E \leftarrow E \cup \{(x_{min}, x_{new})\}\)とする
  - 処理(2-4-3)：\(x_{new}\)の近傍のノードについて\(x_{new}\)を経由することでより小さなコストで到達できるノードがあれば辺を繋ぎ変える
処理(3)：ゴールに辿り着いたか確認
処理(4)：\(x_{init}\)から\(x_{goal}\)までのパスを計算

RRTとの違いを簡単に言うと、RRTでは\(x_{new}\)と\(x_{nearest}\)をそのまま繋いでグラフに追加していましたが、RRT*では\(x_{new}\)に接続すべきノードは\(x_{nearest}\)とは限らず、周辺のノードも含めて\(x_{init}\)からのコストを考慮して決めるという手法になります。これにより、行き当たりばったりな接続が行われなくなるため、かなり最適なルートを得ることができるようになりました。

その他には、\(x_{new}\)に到達可能な最小コストのルートで繋いだことで、\(x_{new}\)を経由すればより低コストで到達できるようになるノードがグラフの中にでてくるかもしれないので、その更新プロセスも存在するというのが特徴です。

プログラム

前回の記事で使用したリポジトリと同じものを使わせていただきます。MITライセンスで公開されています。

本記事ではこれをGoogle Colabで実行してみたいと思います。

前準備（前回の記事と同じ）

Google Colabを開き、今回使用する上記のリポジトリをクローンするとともに、必要なライブラリもインストールします。Google Colabは基本的なライブラリがインストールされた状態になっているので、別途必要なのはrtreeだけでした。また、リポジトリの中のスクリプトをインポートできるようにパスを通しておきます。

!pip install rtree
!git clone https://github.com/motion-planning/rrt-algorithms.git

# パスを通す
import sys
sys.path.append("/content/rrt-algorithms/")

プログラムを一部変更します。

クローンしたリポジトリの中にふくまれているrrt-algorithms/src/utilities/plotting.pyをダブルクリックをして開くと、

self.filename = "../../output/visualizations/" + filename + ".html"が見つかると思いますが、Colab環境では上手く動作しないため、self.filename = filename + ".html"に変更します。変更したら、Ctrl + Cで保存しましょう。

プログラムを開くのが面倒な場合は、以下のコマンドを使って書き換えても問題ありません。

!sed -i 's/"..\/..\/output\/visualizations\/"\ +//g' /content/rrt-algorithms/src/utilities/plotting.py

これで利用する準備だ整いました。

サンプルプログラムを試す

上記のリポジトリには、サンプルプログラムが入っているので、それを参考に一部（障害物情報）変更したものをColabのセルで実行してみます。

以下のプログラムを実行して、必要なものをインポートしましょう。

import numpy as np

from src.rrt.rrt_star import RRTStar  # RRT*クラス
from src.search_space.search_space import SearchSpace
from src.utilities.plotting import Plot

RRT探索における各種パラメータと探索空間の設定をします。今回は、はじめから3次元における探索を試したいと思います。

# 空間設定を3次元平面上の一辺が140の立方体とする
X_dimensions = np.array([(0, 140), (0, 140), (0, 140)])  # dimensions of Search Space
# 障害物情報。これは直方体の始点座標と終点座標の組み合わせ。
Obstacles = np.array(
    [(20, 20, 20, 40, 40, 40), (20, 20, 60, 40, 40, 80), (20, 20, 100, 40, 40, 120),
     (20, 60, 20, 40, 80, 40), (20, 60, 60, 40, 80, 80), (20, 60, 100, 40, 80, 120),
     (20, 100, 20, 40, 120, 40), (20, 100, 60, 40, 120, 80), (20, 100, 100, 40, 120, 120),
     (60, 20, 20, 80, 40, 40), (60, 20, 60, 80, 40, 80), (60, 20, 100, 80, 40, 120),
     (60, 60, 20, 80, 80, 40), (60, 60, 60, 80, 80, 80), (60, 60, 100, 80, 80, 120),
     (60, 100, 20, 80, 120, 40), (60, 100, 60, 80, 120, 80), (60, 100, 100, 80, 120, 120),
     (100, 20, 20, 120, 40, 40), (100, 20, 60, 120, 40, 80), (100, 20, 100, 120, 40, 120),
     (100, 60, 20, 120, 80, 40), (100, 60, 60, 120, 80, 80), (100, 60, 100, 120, 80, 120),
     (100, 100, 20, 120, 120, 40), (100, 100, 60, 120, 120, 80), (100, 100, 100, 120, 120, 120)]
)
x_init = (0, 0, 0)  # スタート位置
x_goal = (140, 140, 140)  # ゴール位置

# 空間設定と障害物情報から実際の探索空間を作成
X = SearchSpace(X_dimensions, Obstacles)

# ===ここまではRRTと同じ===

# RRT*で新たに追加されたパラメータ
rewire_count = 32  # optional, number of nearby branches to rewire

上記のコードはRRTとほぼ同じです。異なるのは、新たにrewire_countパラメータが追加されている点だけです。

# RRT*で探索
rrt = RRTStar(X, Q, x_init, x_goal, max_samples, r, prc, rewire_count)
path = rrt.rrt_star()

可視化します。

plot = Plot("rrt_star_3d")
plot.plot_tree(X, rrt.trees)
if path is not None:
    plot.plot_path(X, path)
plot.plot_obstacles(X, Obstacles)
plot.plot_start(X, x_init)
plot.plot_goal(X, x_goal)
plot.draw(auto_open=False)

htmlファイルが生成されるので、表示してみます。

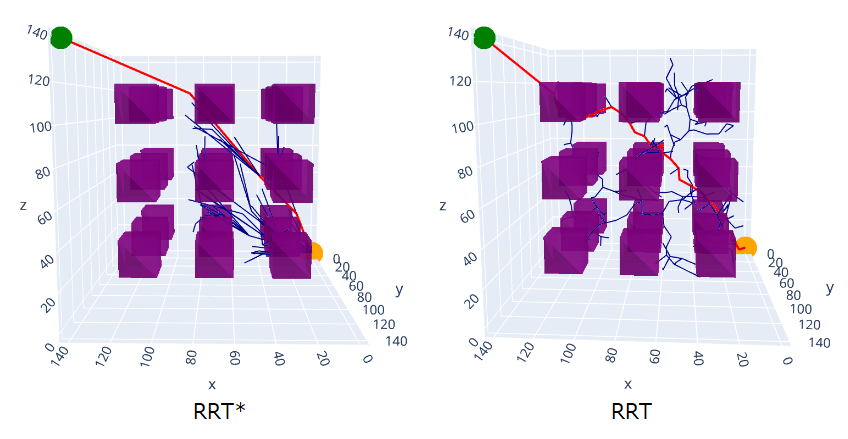
前回の記事でも同じく3次元空間におけるプランニング結果を載せました。比較できるように以下に再掲します。

ある方向から見たときのパスを比較してみます。RRT（右）はランダムに進む方向を決めているため、無駄の多いパスに見えますが、RRT*はほぼ無駄のないパスを探索できているように見えます。

さいごに

RRTを改良した、ある程度最適なパスを生成できるRRT*について解説しました。

RRTやRRT*はロボットアームの軌道生成などで使用される方法なので、頭の片隅に置いておきたいと思います。

RRTの欠点を改善したRRT*とは

RRT

RRT*

RRT*アルゴリズム

プログラム

前準備（前回の記事と同じ）

サンプルプログラムを試す

さいごに

関連

【図解】運動学入門：順運動学と逆運動学について解説！

［Weekly RL with code］DQNでCartPole問題を解く

直感で理解するLSTM・GRU入門 - 機械学習の基礎をマスターしよう！

1次元畳み込みニューラルネットワークでMNISTの時系列処理

【詳説】Attention機構の起源から学ぶTransformer

AGIRobots Blog