この内容の解説はYouTubeにも載せてあります。また、説明やコードは以下で公開しています。
ラグランジュ補完¶
今回はラグランジュ多項式についてポイントをまとめ、Pythonを使用したプログラムを用意した。
結論¶
ラグランジュ補完とは点$(x_0, y_0)\cdots(x_Ny_N)$が与えられたとき、ラグランジュ補完多項式
$$p_N(x) = \sum_jy_jl_j(x)$$
ただし、
$$l_j(x) = \prod_{i, i\neq j}\frac{x-x_i}{x_j - x_i}$$
で補完することをラグランジュ補完という。
元の式を$y_i$の線形結合で近似しているイメージだ。$N+1$個の点が与えられたとき、$N$次の多項式で、元の関数を推測できる。
※補完とは与えられた点と点の間を補うこと。
$l_j(x)$には面白い性質があり、
$$l_j(x_i)=\left\{
\begin{array}{cc}
1&(i= j)\\
0&(i\neq j)
\end{array}
\right.
$$である。 $\forall(x_i, y_i)$ただし$0\le i\le N$を通ればいいよ~という制約のみで式が導出できる。そのため、特定の関数のフィッティングではルンゲの現象といわれる発散が起こることが知られており、注意が必要である。
Pythonで実験¶
補完の例として正弦波関数、標準正規分布の確率密度関数、ルンゲの現象の例として$\frac{1}{1 + 25x^2}$のラグランジュ補完を行ってみる。
正弦波関数の補完¶
必要なライブラリを読み込む
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
f(x)の形を使用して簡単にプロットする関数plot_f()を定義するために、関数f(x)を定義する。
def f(x):
return np.sin(x)
def plot_f(x_min, x_max, y_min, y_max):
x = np.linspace(x_min, x_max, 100)
y = f(x)
plt.plot(x, y, color='blue', label='right graph')
plt.grid()
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xlabel('x')
plt.ylabel('f(x)')
plot_f(-3.5, 3.5, -1.2, 1.2)
x = np.linspace(-3.5, 3.5, 10)
y = f(x)
# 標本点の位置を確認
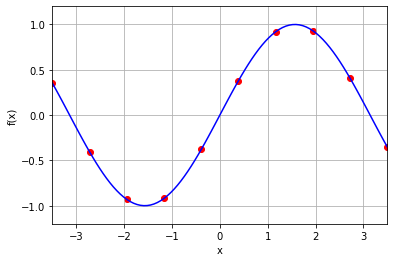
plot_f(-3.5, 3.5, -1.2, 1.2)
plt.scatter(x, y, marker='o', color='red')
class l:
def __init__(self, x_sp, j):
self.x_sp = x_sp
self.j = j
def cal(self, x):
bunshi_ = x - self.x_sp
bunbo_ = self.x_sp[self.j] - self.x_sp
bunshi = 1
bunbo = 1
for i in range(len(self.x_sp)):
if i != self.j:
bunshi *= bunshi_[i]
bunbo *= bunbo_[i]
return bunshi/bunbo
# ラグランジュ補完の関数関数を作成
def LI(x, x_sp, y_sp, num): # numは点の数
L = [] # 係数L
for j in range(num):
L.append(l(x_sp, j))
ans = 0
for i in range(num):
ans += (L[i].cal(x) * y_sp[i])
return ans
xx = np.linspace(-3.5, 3.5, 1000)
yy = []
for x_ in xx:
yy.append(LI(x_, x, y, len(x)))
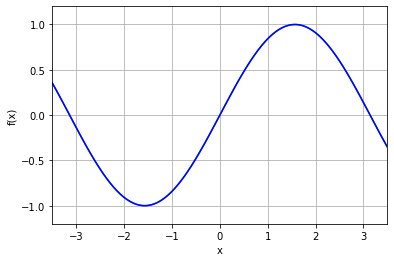
補完の結果
plt.plot(xx, yy)
plot_f(-3.5, 3.5, -1.2, 1.2)
標準正規分布の確率密度関数の補完¶
from scipy.stats import norm
def f(x):
return norm.pdf(x, loc=0, scale=1)
plot_f(-3.5, 3.5, -0.1, 0.5)
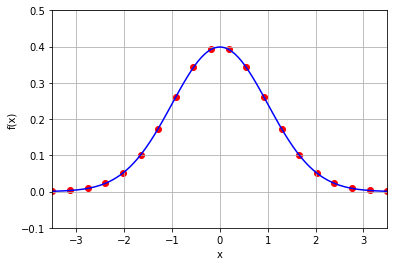
x = np.linspace(-3.5, 3.5, 20)
y = f(x)
plot_f(-3.5, 3.5, -0.1, 0.5)
plt.scatter(x, y, marker='o', color='red')
xx = np.linspace(-3.5, 3.5, 1000)
yy = []
for x_ in xx:
yy.append(LI(x_, x, y, len(x)))
補完の結果
plt.plot(xx, yy)
plot_f(-3.5, 3.5, -0.1, 0.5)
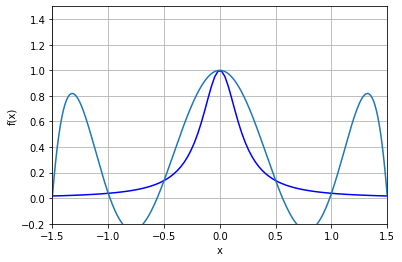
$\frac{1}{1+25x^2}$の補完(ルンゲの減少を確かめる)¶
def f(x):
return 1/(1+25*x**2)
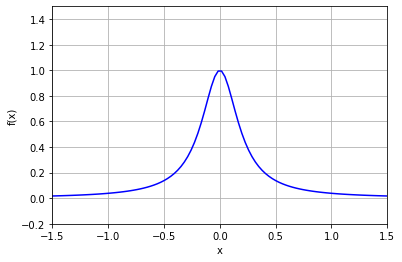
plot_f(-1.5, 1.5, -0.2, 1.5)
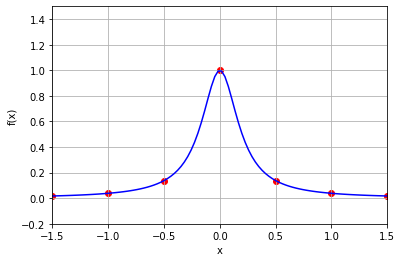
x = np.linspace(-1.5, 1.5, 7)
y = f(x)
plot_f(-1.5, 1.5, -0.2, 1.5)
plt.scatter(x, y, marker='o', color='red')
xx = np.linspace(-1.5, 1.5, 1000)
yy = []
for x_ in xx:
yy.append(LI(x_, x, y, len(x)))
補完の結果
plot_f(-1.5, 1.5, -0.2, 1.5)
plt.plot(xx, yy)
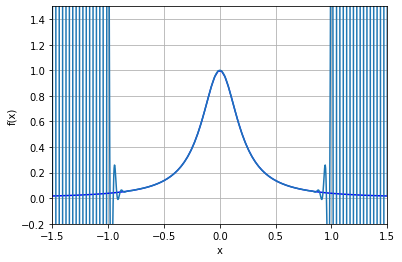
この関数のラグランジュ補完において、Nを無限大にすると、-1および1付近で発散することが知られている。確認としてNを100にする。
x = np.linspace(-1.5, 1.5, 100)
y = f(x)
xx = np.linspace(-1.5, 1.5, 1000)
yy = []
for x_ in xx:
yy.append(LI(x_, x, y, len(x)))
plot_f(-1.5, 1.5, -0.2, 1.5)
plt.plot(xx, yy)
ルンゲの現象が確認できた。
まとめ¶
元の関数がわからない状態で補完をしていくことが、メインの使用方法になるし、そのためのラグランジュ補完なのだが、関数によってはNを大きくすると発散してしまうことが分かる。そのため、上記の例の関数から得られる標本点のような特徴を持っているのかわからないものについては、Nを大きくしすぎないことが望ましいと考えられる。