本記事では、Highway Networkについて解説していきます。
導入
ニューラルネットワークは層を深くすることで大きな成功を手に入れてきました。
しかし、層が深くなればなるほど誤差が入力層側へ伝わらず学習が難しくなるという大きな問題を抱えていました。
これを解決した最も有名なアーキテクチャはResNetです。
また、ResNetに似た考え方の元、発表されたネットワークは沢山あり、そのひとつにHighway Networkがあります。本記事では、Highway Networkを紹介します。
Highway Network
Highway Networkの構造
最も基本的なHighway Networkは以下の式で表現される層のアーキテクチャを持っています。
$$
\boldsymbol{y} = H(\boldsymbol{x}, \boldsymbol{W_H})\odot T(\boldsymbol{x}, \boldsymbol{W_T})+ \boldsymbol{x}\odot C(\boldsymbol{x}, \boldsymbol{W_C})
$$
ここで、\(H(\boldsymbol{x}, \boldsymbol{W_H})\)、\(T(\boldsymbol{x}, \boldsymbol{W_T})\)、\(C(\boldsymbol{x}, \boldsymbol{W_C})\)はそれぞれ重み行列\(\boldsymbol{W_H}、\boldsymbol{W_T}、\boldsymbol{W_C}\)をもつニューロンを表しています。一般的に、ニューロンはアフィン変換と活性化関数により、
$$
f(\boldsymbol{W}^T\boldsymbol{x} + \boldsymbol{b})
$$
と表現されるのが一般的ですが、この論文ではそれを拡張した表記を使用しています。この式から、1層の処理に複数の種類のニューロン層が関与していることがわかりますが、層のメイン出力を与えるニューロンは、\(H(\boldsymbol{x}, \boldsymbol{W_H})\)で、そこに、skip-connection(\boldsymbol{x})があり、これら2つのパスをどの程度出力に反映させるかを2つのゲートニューロン\(T(\boldsymbol{x}, \boldsymbol{W_T})\)と\(C(\boldsymbol{x}, \boldsymbol{W_C})\)で制御していると考えることができます。ちなみに、ゲートニューロンの出力は\((0,1)\)を想定しています。
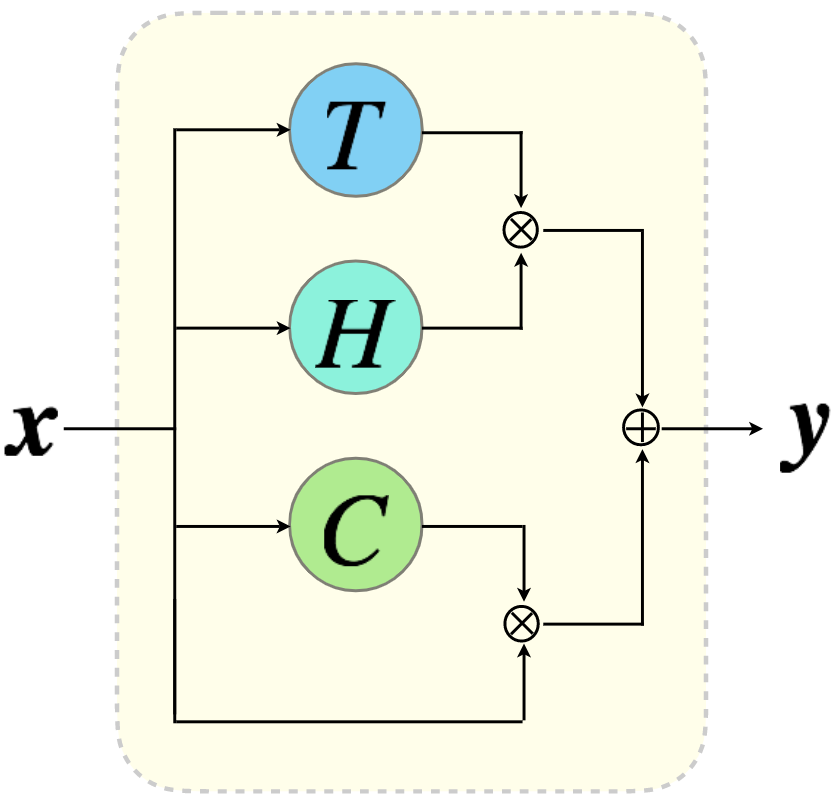
図から、メインニューロン\(H\)のパスと入力\(\boldsymbol{x}\)がそのまま通過するパスが、ゲートニューロン\(T\)と\(C\)によりそれぞれアダマール積され、それらが結合されたものが出力になることがご理解いただけると思います。
ここまで示してきた基本的なHighway Networkは、ある工夫をすることで、パラメータ数を少なくすることができます。その工夫とは、ニューロン\(C\)を\(1-T\)で置き換えてしまうことです。このとき、先ほどの式は、
$$
\boldsymbol{y} = H(\boldsymbol{x}, \boldsymbol{W_H})\odot T(\boldsymbol{x}, \boldsymbol{W_T})+ \boldsymbol{x}\odot (1 - T(\boldsymbol{x}, \boldsymbol{W_T}))
$$
で書き表すことができます。ゲートニューロンの活性化関数には、シグモイド関数を使用するため、出力が0もしくは1に漸近することはあれど、その値になることは数学的にはあり得ませんが、コンピュータに計算過程で発生する誤差により、0もしくは1になることはあり得ます。そこで、ゲートニューロンの層がすべて0もしくは1(ベクトルで表記すれば\(\boldsymbol{0}\)もしくは\(\boldsymbol{1}\))の場合、以下のような式で表すことができます。
$$
\boldsymbol{y} =
\begin{cases}
\boldsymbol{x}&if\ \ T(\boldsymbol{x}, \boldsymbol{W_T}) = \boldsymbol{0}\\
H(\boldsymbol{x}, \boldsymbol{W_H})&if\ \ T(\boldsymbol{x}, \boldsymbol{W_T}) = \boldsymbol{1}
\end{cases}
$$
$$
\frac{d \boldsymbol{y}}{d \boldsymbol{x}} =
\begin{cases}
\boldsymbol{I}&if\ \ T(\boldsymbol{x}, \boldsymbol{W_T}) = \boldsymbol{0}\\
H'(\boldsymbol{x}, \boldsymbol{W_H})&if\ \ T(\boldsymbol{x}, \boldsymbol{W_T}) = \boldsymbol{1}
\end{cases}
$$
これらの式から、Highway Networkはskip-connectionを持つResNet的構造をとったり、skip-connectionを持たない単純なネットワーク構造をとったりすることができることがわかります。
Highway NetworkとResNet
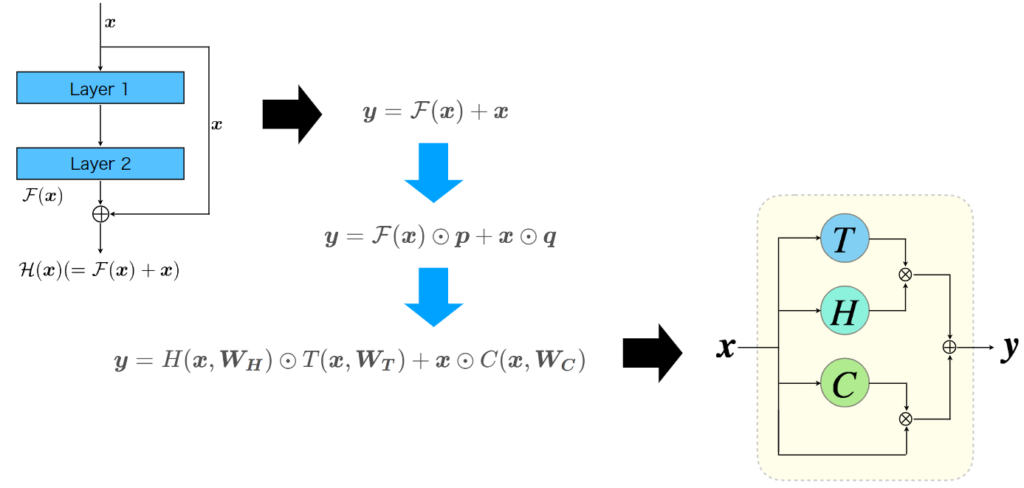
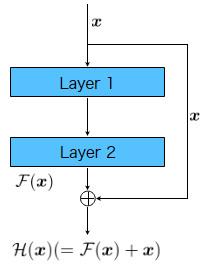
ResNetは、層が恒等写像を学習するのは難しいということで、skip-connectionにより恒等写像のパスを並列に用意した残差ブロックを利用しました。これにより、ニューラルネットの層自体は残差を学習します。数式で表すと、残差ブロックが学習したい変換を\(\mathcal H(\boldsymbol{x})\)としたとき、その内部の層が学習する変換\(\mathcal F(\boldsymbol{x})\)は、恒等写像\(\boldsymbol{x}\)と引いたもの、\(\mathcal H(\boldsymbol{x}) - \boldsymbol{x}\)になります。ニューラルネットワークが恒等写像を学習するのが難しいなら、層への入力から恒等写像の成分を抜き去ったものを学習すればいいという解釈も可能だと思います。そのため、残差ブロックの出力\(\boldsymbol{y}\)は
$$
\boldsymbol{y} = \mathcal F(\boldsymbol{x}) + \boldsymbol{x}
$$
と表されます。
ここで、層の出力と恒等写像の出力への反映度をそれぞれ、\((\boldsymbol{0, 1})\)の範囲のベクトル\(\boldsymbol{p}、\boldsymbol{q}\)で調節するようにすると、式は以下のようになります。
$$
\boldsymbol{y} = \mathcal F(\boldsymbol{x})\odot\boldsymbol{p}+ \boldsymbol{x}\odot\boldsymbol{q}
$$
ここで、\(\boldsymbol{q} = \boldsymbol{1-p}\)にすると、
$$
\boldsymbol{y} = \mathcal F(\boldsymbol{x})\odot\boldsymbol{p}+ \boldsymbol{x}\odot(\boldsymbol{1-p})
$$
のようになります。つまり、Highway Networkでは、残差を学習しつつ、ゲートニューロンで、どの程度の情報を通過させるかも学習するということになります。
そして、気になるのが、ResNetより優れているのかということですが、結論を言うと、ResNetの方が優れています。Highway Networkでは、学習によりほぼ完全に恒等写像を消すことができるため、そもそも恒等写像を消すことができないResNetに比べ、大変深い層での学習で精度向上が難しかったのだろうと私は解釈しています。
Highway NetworkとLSTM
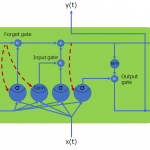
Highway Networkでは、ゲートニューロンにより情報の流れを調節&制限するゲートを利用しています。これは、時系列処理で優れているRNNの一種のLSTMからインスパイアされたものです。
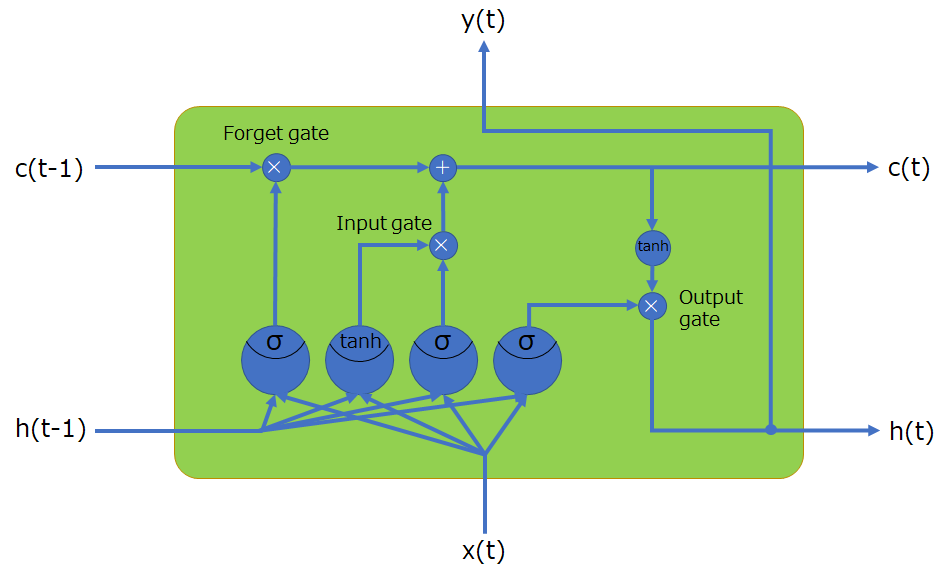
LSTMについて簡単に説明すると、以下の4つ
- 記憶セル(CECセル)
- 入力ゲート・出力ゲート・忘却ゲート
- ゲートを操作するニューロンが3つ
- セルへの入力を求めるニューロンが1つ
で構成されいて、情報をCECセルと呼ばれる記憶セルに保持し、その記憶の更新の際に、どの程度、入力値を反映させるかを決定する入力ゲート、CECセルをどの程度忘却させるかを決定する忘却ゲート、CECセルの情報をどの程度出力へ流すかを決定する出力ゲートから構成されています。ちなみに、上図のLSTMは時間軸で展開したものになっています。
詳しい内容につきましては、以下の記事で解説しています。
このように、ゲートニューロンを用意して、情報の流れを制御するという手法はLSTMと同じです。
まとめ
Highway Networkは、ResNetと似ていて、skip-connectionによる恒等写像の構造を持ちます。ResNetでは、恒等写像を反映する程度を調節できませんが、Highway Networkでは調節が可能です。式からは、ResNetと今までの古典的なネットワークをより一般化したものと解釈が可能です。しかし、柔軟性を向上させることばかりが性能向上に寄与するとは限らず、ResNetのように思い切った構造をとる方が性能が良い場合もあります。ゲートニューロンによる情報の流量を調節するというのは、強力で有用な手法であることは経験的にわかっているため、今後も、このようなネットワークは登場してくると思います。
参考文献
R. K. Srivastava, K. Greff, J. Schmidhuber. Highway Networks. arXiv:1505.00387.