畳み込み層の計算コストを大幅に軽減することができる理想的な畳み込み手法があると言われたら何が思い浮かびますか?
色々な解決手法が提案されていますが、今回は、その中でもMobileNetと呼ばれる畳み込みニューラルネットワークで使用されているDepthwise Separable Convolutionについて説明します。
MobileNetとはスマートフォンなどの計算資源の小さいマシンで使うことを想定し、計算コストが小さくなるように設計された畳み込みニューラルネットワークです。従来の畳み込みニューラルネットワークで使用される畳み込み層は計算コストが高いため高性能なGPUを積んだマシンでしか現実的な時間内で利用することはできませんでした。そこで、畳み込み層の性能を極力落とさずに計算コストを改善しようとして提案された畳み込み手法の1つが今回説明するDepthwise Separable Convolutionです。Depthwise Separable Convolutionの要素技術は、Depthwise ConvolutionとPointwise Convolutionの2つだけとなっており、本記事をお読みいただければ十分に理解ができると思います。
それでは、Depthwise Separable Convolutionについて分かりやすく解説していきます!
畳み込みニューラルネットワーク
まず最初に畳み込みニューラルネットワーク(Convolutional Neural Network: CNN)について簡単に説明します。畳み込みニューラルネットワークについて詳しく知りたい方は以下の記事を参考にしてください。
畳み込みニューラルネットワークとは、主に画像分野で使用される深層ニューラルネットワークです。畳み込み層とプーリング層を用いて画像特徴を抽出し、回帰や分類などを実現します。下図に畳み込みニューラルネットワークの概略を示します。
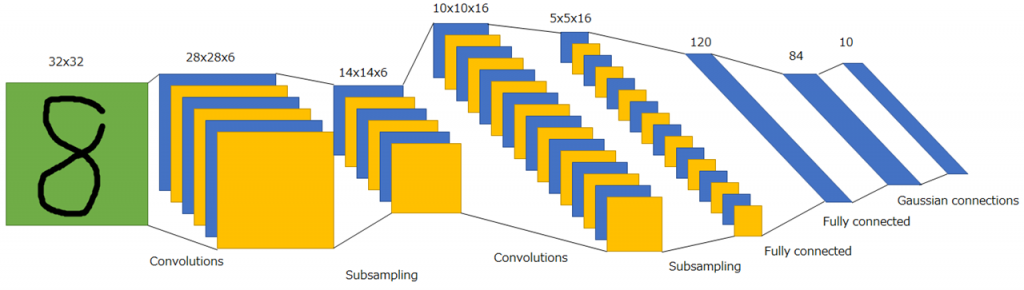
畳み込みニューラルネットワークでは、畳み込み層とプーリング層を繰り返し適用しますが、何度も適用する過程で、画像特徴が抽出され、最終的には1次元のベクトルにして全結合層(fully connected layer)に入力するのが定石となっています。畳み込みニューラルネットワークの起源はネオコグニトロン(Neocognitron)とされています。これは学習に自己組織化を用いており、現在の学習アルゴリズムの枠組みで学習できないため、それを現在の機械学習手法の枠組みで学習可能にしたのがLeNetとなっています。このような理由からLeNetが畳み込みニューラルネットワークの起源であると主張する人もいます。
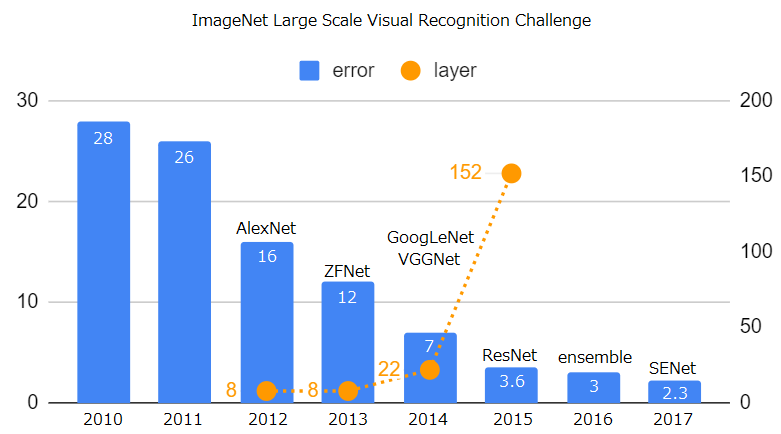
畳み込みニューラルネットワークは、深層学習ブームの火付け役でもあります。2012年に行われたILSVRCと呼ばれる画像認識コンペでAlexNetという畳み込みニューラルネットワークが大きな成果を上げたことで、深層学習ブームに火が付きました。AlexNetの登場以降、VGGやGeegleNet、ResNetなど様々なニューラルネットワークが登場しました。下図は、ILSVRCにおける優勝モデルの変遷です。精度の向上はネットワークの総数の増加と大きく関係があります。基本的に総数が増加すればパラメータの数も増加するため、大きな計算資源が必要になります。
畳み込みニューラルネットワークの変遷については、以下の動画で詳しく説明していますのでぜひご視聴ください!
畳み込み層の処理
畳み込みニューラルネットワークを構成する重要な構成要素に畳み込み層とプーリング層があります。畳み込み層では画像の特徴を検出し、プーリング層では検出された特徴の位置ずれを許容する働きがあります。ここでは、畳み込み層に焦点を当て、その畳み込み処理について解説します。
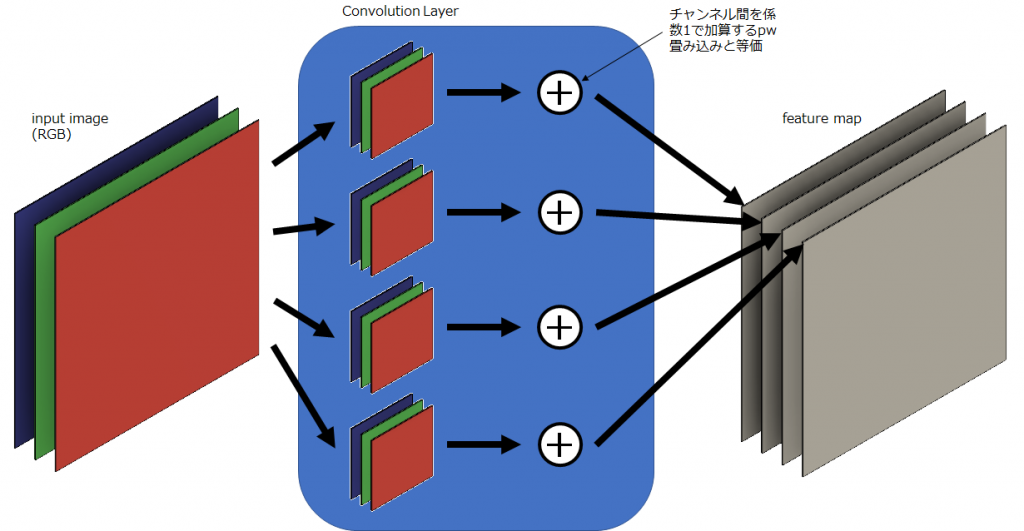
畳み込み層は複数の畳み込みフィルタから構成されます。また、各々の畳み込みフィルタはチャネル方向の成分を持っており、これは複数枚のフィルタから構成されていることを意味します。下図のように、入力特徴マップとしてチャンネル数が3のRGB画像を、畳み込み処理を適用してチャンネル数が4の特徴マップに変換される場合を仮定します。下図は一般的な畳み込み層による畳み込み処理を図示したもので、背景が青色で塗られている領域が畳み込み層による処理を表しています。この場合に使用される畳み込みフィルタの数は、変換後の特徴マップのチャンネル数と同じになるので4つです。各々の畳み込みフィルタのチャンネル数は入力特徴マップのチャンネル数と同じなので3つです。すなわち、入力特徴マップのチャンネル数から、各々の畳み込みフィルタのチャンネル数が決まり、出力特徴マップのチャンネル数から、畳み込みフィルタの数が決まります。一般的に、これらは一意に決まります。
上の図を一般化したものを以下に示します。下図では、入力特徴マップのサイズを\((H^{l-1}, W^{l-1}, C^{l-1})\)、出力特徴マップのサイズを\((H^l, W^l, C^l)\)としています(Channel Last表記)。このとき、各々の畳み込みフィルタのチャンネル数は\(C^{l-1}\)、畳み込みフィルタの数は\(C^l\)になります。これは以前の記事でも解説しました。
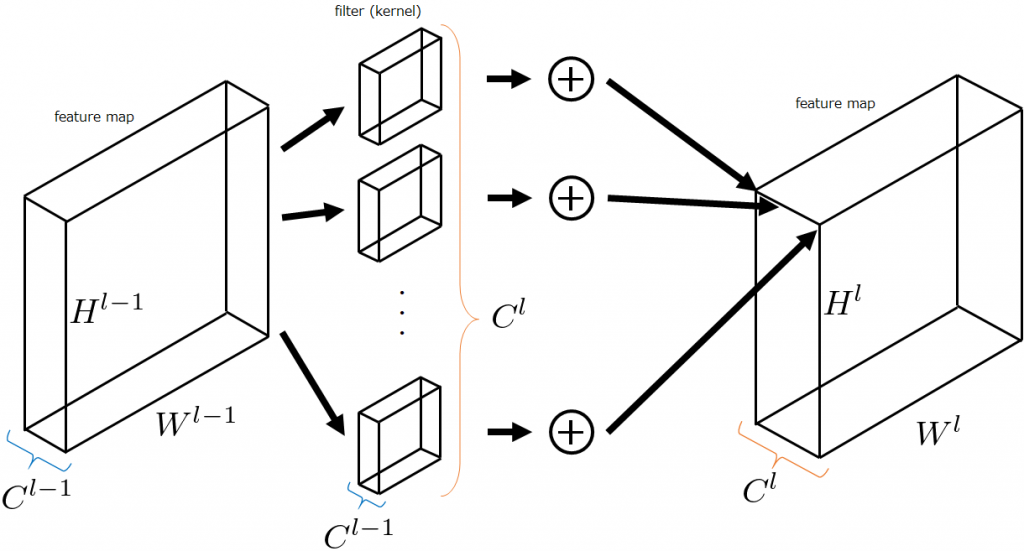
畳み込みニューラルネットワークでは、層が深くなるにつれて特徴抽出が進み、出力特徴マップのチャンネル数が大きくなります。すると、計算コストが膨大になることが直感でも分かると思います。
最近はスマートフォンなどのモバイル機器のCPUやGPU、NPUなどのプロセッサの性能向上が目覚ましいですが、当時はそこまででありませんでした。その為、計算コストを小さくする工夫が必要になりました。様々な工夫が考えられますが、今回説明するDepthwise Separable Convolutionでは、一般的な畳み込み処理をDepthwise ConvolutionとPointwise Convolutionに分けることで、入出力のサイズは一般的な畳み込みと同様でありながら、大幅な計算コストの改善を実現しました。
Depthwise Separable Convolutionの処理
Depthwise Separable Convolutionとは、一般的な畳み込み層の処理をDepthwise ConvolutionとPointwise Convolutionに分けたものです。それでは、それぞれの畳み込み処理がどのように行われるのか説明していきます。
下図にDepthwise Separable Convolutionによる畳み込みを示します。先ほど示した図において背景が青色の領域が2つに分かれています。もっとも分かりやすいところを言うと、前半の畳み込みフィルタの数が1つになっています。Depthwise Separable Convolutionでは前半部分は出力特徴マップのチャンネル数に依存せず常に1つです。よく見ると後半の処理も若干変わっています。一般的な畳み込み層では、前半の各々の畳み込みフィルタで計算された結果をチャンネル方向に足し合わせる(全重み1による重み付和という解釈は可能)処理をしますが、Depthwise Separable Convolutionでは後半で学習によりチューニング可能なパラメータを持つ重み付和として計算をします。前半で畳み込みフィルタの数を減らしパラメータ数を大幅にカットし、後半に学習パラメータを追加したのです。これにより前半の計算コストの改善は大きく、例えば、出力特徴マップのチャンネル数が256なら、256個の畳み込みフィルタが必要だったのが、Depthwise Separable Convolutionでは1つでよくなりました。Depthwise Separable Convolutionでは、前半の畳み込み処理をDepthwise Convolution、後半の畳み込み処理をPointwise Convolutionと呼びます。Depthwiseとは深さ単位、Pointwiseとは点単位と訳すことができるように、Depthwise Convolutionは深さ単位で畳み込みを、Pointwise Convolutionは点単位(=ピクセル単位)で畳み込みをします。
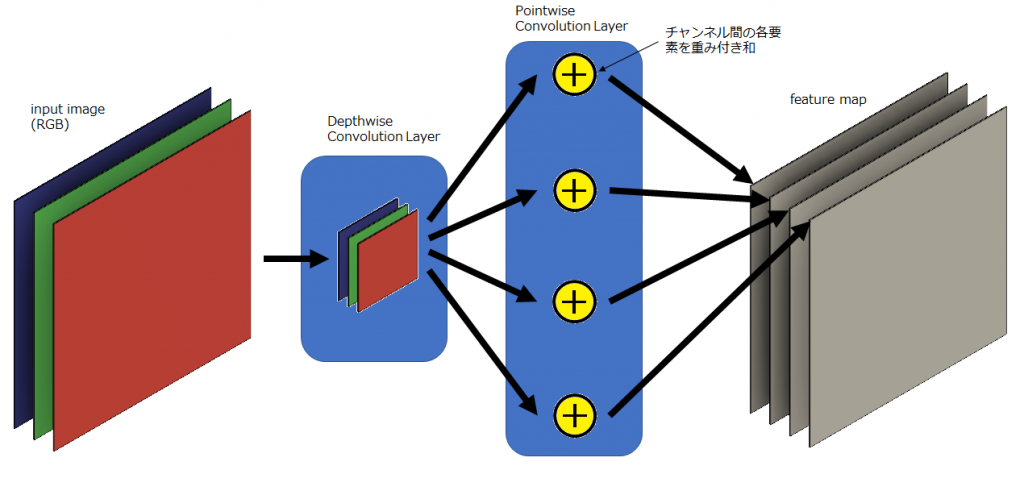
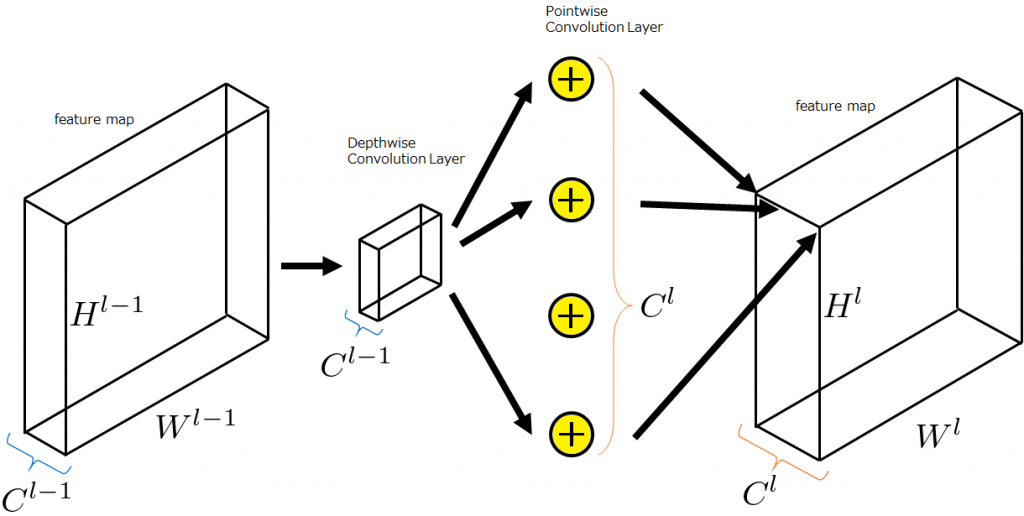
これを先ほどと同様に一般化したいと思います。下図のようにそれぞれのサイズを文字で置きます。まず、入力特徴マップ\((H^{l-1}, W^{l-1}, C^{l-1})\)はチャンネル数が\(C^{l-1}\)のDepthwise Convolutionにより、\((H^l, W^l, C^{l-1})\)に変換されます。次に、チャンネル数\(C^{l-1}\)の\(C^l\)個のPointwise Convolutionにより、特徴マップ\((H^l, W^l, C^l)\)が出力されます。
一般的な畳み込みとDepthwise Separable Convolutionの比較
基本事項
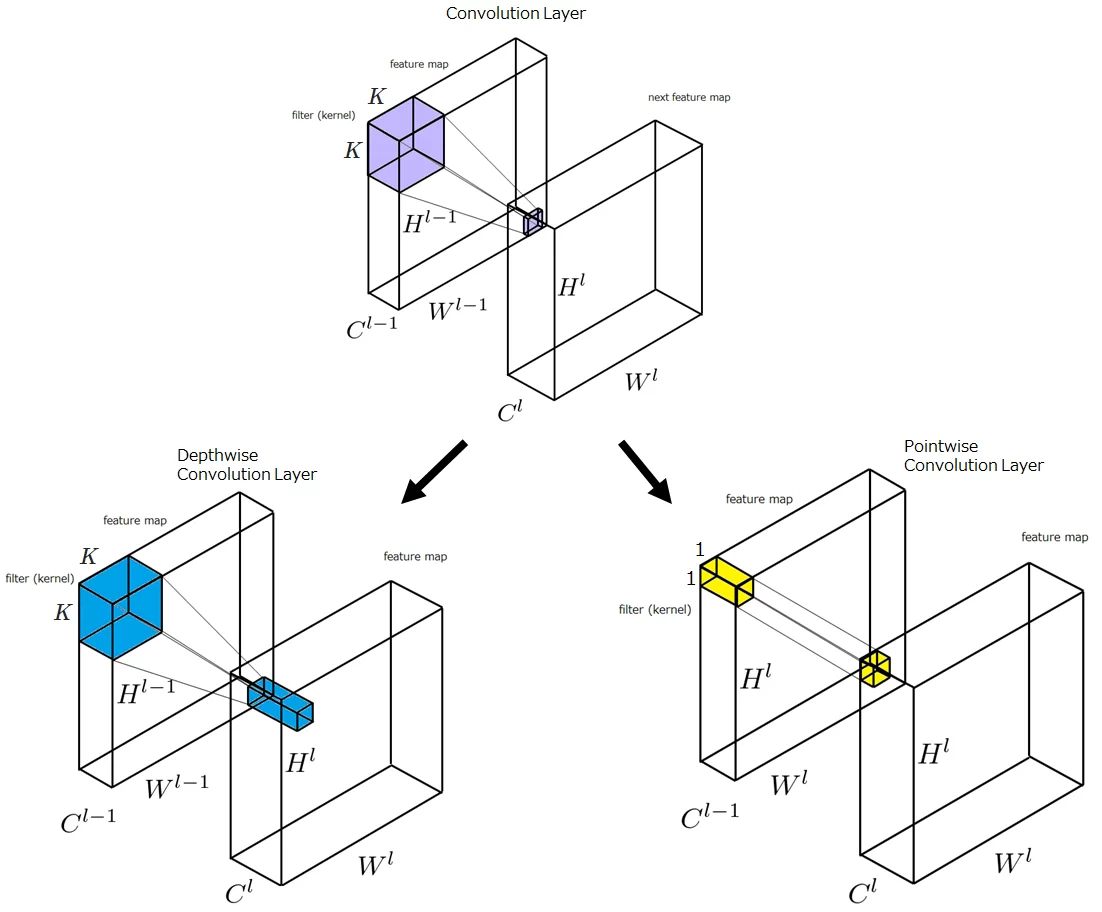
下図は、入力特徴マップから出力特徴マップへ変換するときの、畳み込み層の入力領域と出力領域の関係を示しています。
図中、Convolution Layerと記載がある部分は、一般的な畳み込み層の処理を表しており、入力特徴マップの一箇所のパッチ\((K,K,C^{l-1})\)にフィルタを適用すると、出力特徴マップの1箇所\((1,1,1)\)の値に写像されることが分かります。
Depthwise Convolution Layerと記載がある部分は、Depthwise Convolutionの処理を表しており、入力特徴マップの一箇所のパッチ\((K,K,C^{l-1})\)にフィルタを適用すると、出力特徴マップの1箇所のパッチ\((1,1,C^l)\)に写像されることが分かります。
Pointwise Convolution Layerと記載がある部分は、Pointwise Convolutionの処理を表しており、入力特徴マップの一箇所のパッチ\((1,1,C^{l-1})\)にフィルタを適用すると、出力特徴マップの1箇所\((1,1,1)\)の値に写像されることが分かります。
Depthwise Convolutionの後にPointwise Convolutionを行うと、\((K,K,C^{l-1})\)から\((1,1,1)\)への変換と、入出力の特徴マップの関係は、一般的な畳み込みと同じになるので、一般的な畳み込み層をこれで置き換えることが可能になります。これが、Depthwise Separable Convolutionです。
それでは、一般的な畳み込みとDepthwise Separable Convolutionについて、計算式や計算コストについて確認し比較してみます。
計算式
それでは一般的な畳み込みとDepthwise Separable Convolutionの計算式を導出していきます。まずは、一般的な畳み込みにおいて入力および出力特徴マップ、畳み込みフィルタを以下のように仮定します(Channel Last形式で記載しています)。
- 入力特徴マップ\(I^{l-1}\): \((H^{l-1}, W^{l-1}, C^{l-1})\)
- 出力特徴マップ\(I^l\): \((H^l, W^l, C^l)\)
- 畳み込みフィルタ\(F\): \((K, K, C^{l-1})\)(ただし\(K=2N^{l-1} + 1\))
このとき、一般的な畳み込み層は以下に示す計算式で表されます。
$$
I_{xym}^l=\sum_{k=1}^{C^{l-1}}\sum_{i=-N^{l-1}}^{N^{l-1}}\sum_{j=-N^{l-1}}^{N^{l-1}}I^{l-1}_{sx+i, sy+j, k}F_{i+N^{l-1}, j+N^{l-1},k,m}
$$
\(s\)はストライド、\(k\)は入力特徴マップにおいて注目しているチャンネル、\(m\)は出力特徴マップにおいて注目しているチャンネルです。\(\sum_{k=1}^{C^{l-1}}\)は各々の畳み込みフィルタによって計算された値をチャンネル方向に重み1で足し合わせる操作です(全ての重みが1のPointwise Convolutionに対応)。\(\sum_{i=-N^{l-1}}^{N^{l-1}}\)と\(\sum_{j=-N^{l-1}}^{N^{l-1}}\)は、空間方向の畳み込みをしています(Depthwise Convolutionに類似)。
それでは、この計算式をもとにしてDepthwise Separable Convolutionの計算式を導出します。まず、Depthwise Convolutionでは畳み込みフィルタの数は1つなので、\(F_{i+N^{l-1}, j+N^{l-1},k,m}\)から\(m\)を取り除き、\(F_{i+N^{l-1}, j+N^{l-1},k}\)にします。Pointwise Convolutionは、重みパラメータを持ち、また、出力特徴マップの深さ\(m\)に位置する値を計算するため、\(m\)番目のPointwise Convolutionの\(k\)番目の重みパラメータを\(w_{k,m}\)と置きます。このとき、Depthwise Separable Convolutionの計算式は以下のようになります。
$$
I_{xym}^l=\sum_{k=1}^{C^{l-1}}w_{k,m}\left\{\sum_{i=-N^{l-1}}^{N^{l-1}}\sum_{j=-N^{l-1}}^{N^{l-1}}I^{l-1}_{sx+i, sy+j, k}F_{i+N^{l-1}, j+N^{l-1},k}\right\}
$$
\(\{\}\)の中がDepthwise Convolutionで外側がPointwise Convolution(正確にはDepthwise Convolutionで計算されたもののうち、\(k\)番目のチャンネルの\((x, y)\)成分)です。\(m\)が外側へ移動したので、繰り返しの計算回数が大幅に減少しました。
計算コスト
それでは一般的な畳み込みとDepthwise Separable Convolutionの計算コストを比較します。
一般的な畳み込み層の乗算回数およびパラメータ数
1つのパッチに1つのフィルタを適用するときの乗算回数は\(K^2C^{l-1}\)です。入力特徴マップのサイズを\((H^{l-1}, W^{l-1}, C^{l-1})\)、畳み込みフィルタの個数を\(C^l\)、ストライドを1とすると、全パッチ数は\(H^{l-1}W^{l-1}\)でなので畳み込みフィルタの乗算回数は以下のようになります。
$$
K^2C^{l-1}H^{l-1}W^{l-1}×C^l
$$
そして、パラメータ数は1つのフィルタがもつパラメータ数×フィルタの個数なので
$$
K^2C^{l-1}×C^l
$$
となります。
Depthwise Convolutionの乗算回数およびパラメータ数
Depthwise Convolutionは、畳み込みフィルタの個数は1つなので、以下の式になります。
$$
K^2C^{l-1}H^{l-1}W^{l-1}
$$
パラメータ数は
$$
K^2C^{l-1}
$$
となります。
Pointwise Convolutionの乗算回数およびパラメータ数
Pointwise Convolutionは、1x1の畳み込みなので、以下のような式で表されます。
$$
C^{l-1}H^lW^l×C^l
$$
パラメータ数は
$$
C^{l-1}C^l
$$
となります。
Depthwise Separable Convolutionの魅力
先ほど求めた乗算回数とパラメータ数を表にまとめると以下の表になります。

これを用いて、一般的な畳み込みとDepthwise Separable Convolutionの乗算回数とパラメータ数を比較します。
一般的な畳み込み(Standard-Convと表記)、Depthwise Separable Convolution(Depth-Sep-Convと表記)の乗算量及びパラメータ数の比を計算してみます。以下では計算式を簡単にするために、\(W^{l-1} = H^{l-1} = W^l = H^l = D\)と置いています。
$$
\begin{eqnarray}
\begin{array}{rcl}
&&\frac{Depth-Sep-Conv\mbox{の乗算回数}}{Standard-Conv\mbox{の乗算回数}}\\
&=&\frac{K^2C^{l-1}D^2 + C^{l-1}D^2×C^l}{K^2C^{l-1}D^2×C^l}\\
&=&\frac{1}{C^l} + \frac{1}{K^2}
\end{array}
\end{eqnarray}
$$
また、パラメータ数の比較を行うと
$$
\begin{eqnarray}
\begin{array}{rcl}
&&\frac{Depth-Sep-Conv\mbox{のパラメータ数}}{Standard-Conv\mbox{のパラメータ数}}\\
&=&\frac{K^2C^{l-1} + C^{l-1}C^l}{K^2C^{l-1}×C^l}\\
&=&\frac{1}{C^l} + \frac{1}{K^2}
\end{array}
\end{eqnarray}
$$
となることが分かります。両方とも比率は同じになります。Pointwise Convolutionの個数\(C^l\)の逆数とDepthwise Convolutionのカーネルサイズの2乗の逆数を線形結合したものとして表されます。
具体的に計算をしてみましょう。ILSVRCなどで使用される畳み込みニューラルネットワークは特徴マップのチャンネル数が100を超すことが多いので、第1項目\(\frac{1}{C^l}\simeq 0\)とできます。フィルタサイズを5x5にすると\(\frac{1}{K^2}=\frac{1}{25}\)になります。すなわち、古典的な畳み込みフィルタを使用するよりも、単純計算で25倍の軽量化に成功できることが分かります。
まとめ
一般的な畳み込みをDepthwise ConvolutionとPointwise Convolutionに分割し、Depthwise Convolutionを1種類にするとで計算コストを大幅に小さくすることに成功たDepthwise Separable Convolution層は、MobileNetを中心に使用されており、性能面でも大差ない、組込みシステムで画像認識をする必要性がある場合は、積極的に使用していきたいですね。
参考文献
Andrew G. Howard, Menglong Zhu, Bo Chen, Dmitry Kalenichenko, Weijun Wang, Tobias Weyand, Marco Andreetto, Hartwig Adam, "MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications," arXiv, 2017.