Deep Learning アドベントカレンダー3日目の記事では、ボルツマンマシンを扱いたいと思います。ボルツマンマシンは、前回扱ったホップフィールドネットワークを拡張したもので、深層学習の原点でもあるので、しっかりと学んでいきたいと思います。
と思ったのですが、ボルツマンマシンの情報が少なすぎで、自分の中で知識が思うように整理できませんでした。制約ボルツマンマシンの情報なら山のように見つかるのですが、、、
この記事は作成途中、つまり仮投稿です。まだ内容がまとまっていません(いくつか間違いがあります)。近いうちに完成させます。ご迷惑おかけして申し訳ありません。記事が完成し次第、動画も投稿します。
アブストラクト
ボルツマンマシンの特徴
- ホップフィールドネットワークの拡張なので、基本的にホップフィールドネットワークの特徴を受け継ぐ
- 確率論的ニューロンを使用する
- ホップフィールドネットワークに比べて局所解に陥りにくい
ボルツマンマシンの欠点
- 組み合わせ爆発が起きるので計算量が現実的ではない
ボルツマンマシンの学習手順
準備
決定論的ニューロン
決定論的ニューロンは入力に対して出力が決定的に決まるニューロンです。つまり、\(y=f(x)\)ということです(左の図)。
確率論的ニューロン
確率論的ニューロンは入力に対して出力が確率的に決まるニューロンです。つまり、\(y~p(f(x))\)ということです(右の図)。

これが何を意味するかというと、0と1の二値出力をするニューロンの場合、決定論的ニューロンなら\(x\)が入力されたら必ず1になる一方で、確率的ニューロンでは確率\(p(f(x))\)で1が、確率\(1-p(f(x))\)で0がでることを意味します。つまり、出力に多少の不確実性があるのです。別の言い方をすれば、確率的なニューロンは、状態に勝手にノイズを付加してくれるってことです。
識別モデルと生成モデル
識別モデルと生成モデルの違い
機械学習モデルには主に識別モデルと生成モデルがあります。以下の図は両者が学習する対象の違いを図示したもので、識別境界線を学習するのが識別モデル、背後にある母集団の確率分布を学習するのが生成モデルです。識別モデルは、識別境界線を学習するため実際に図中の青い標本点や赤い標本点がどのように分布しているかは学習していませんが生成モデルは識別が目的ではなくバックにある母集団がどのように分布しているか推定することで本質的な特徴を学習しようとするため、その母集団の分布さえ学習してしまえば、無限に標本点を生成することができます。
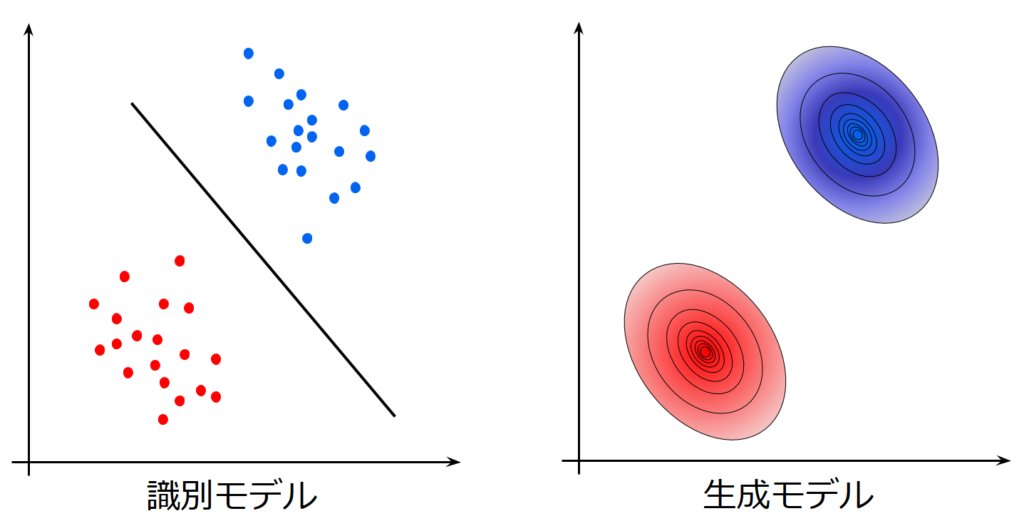
そして、生成モデルは識別に使用することも可能である点も重要です。そのため、現在の深層学習の高性能化、汎化には生成モデルがとても重要なものとなっており、最近ではVAEやGANをはじめとした多くの(深層)生成モデルが生まれています。
識別モデル
ロジスティック回帰という線形識別モデルを使って、先ほどの赤青の分布を識別することを考えます。以下の場合、ロジスティック関数を\(\sigma(x) = \frac{1}{1+ e^{-x}}\)、横軸と縦軸を\(x_1, x_2\)、それらの係数を\(a_1, a_2\)、バイアスを\(b\)として、
$$
y = \sigma(a_1x_1 + a_2x_2 + b)
$$
と表すことができます。そして、パラメータは二乗誤差関数で最適化したとします。
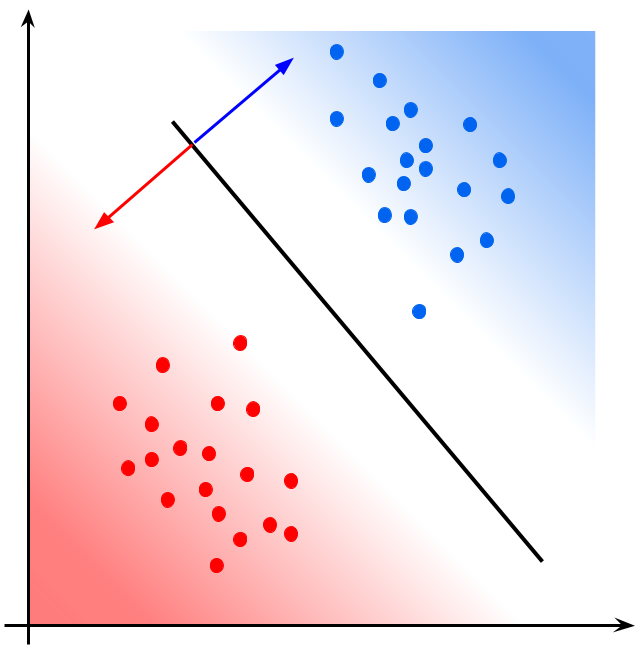
パラメータが最適化された後に、ロジスティック回帰モデルの出力する確率を可視化すると以下のようになります。
識別境界線は、出力\(y=0.5\)となる\((x_1, x_2)\)のグラフとなり、その回帰直線から右上に進むにつれ、青である確率が上昇し、左下に進むにつれて赤である確率が上昇(青である確率が減少)します。確率で考えれば今述べたように境界線を境として滑らかに変化していますが、ロジスティック回帰分析では量子化器により、0.5以上は青、0.5未満は赤といったように二値に写像されます。
その他にも、識別器といわれるものには、パーセプトロンやサポートベクターマシンなどがあります。
生成モデル
生成モデルでは、その標本点が任意の確率分布\(p(\boldsymbol{x})\)に従って生成されていると仮定し、\(p(\boldsymbol{x})\)の近似を求めようとします。より具体的には、真の分布\(p(\boldsymbol{x})\)は求めることができないので、パラメータ\(\boldsymbol{\theta}\)を用意し自由度のある条件付確率分布\(p(\boldsymbol{x}|\boldsymbol{\theta})\)で近似、すなわち、\(\boldsymbol{\theta}\)を決定することで、未知の真の分布を\(p(\boldsymbol{x})~p(\boldsymbol{x}|\boldsymbol{\theta})\)とするのです。なお、いきなり\(p(\boldsymbol{x}|\boldsymbol{\theta})\)を求めるのではなく、ある程度の確率分布を事前に仮定しておきます。例えば、正規分布とかです。この場合は\(p(\boldsymbol{x})~p(\boldsymbol{x}|\boldsymbol{\theta})=\mathcal N(\boldsymbol{x}|\boldsymbol{\mu},\boldsymbol{\sigma}^2)\)となります。このとき、パラメータ\(\boldsymbol{\theta}\)は平均\(\boldsymbol{\mu}\)と分散\(\boldsymbol{\sigma}^2\)だろう思われるかもしれませんが、基本的に平均\(\boldsymbol{\mu}\)と分散\(\boldsymbol{\sigma}^2\)はニューラルネットワークにより求められるので、そのニューラルネットワークの重み\(\boldsymbol{(w_1,\cdots)}\)やバイアス\(\boldsymbol{(b_1,\cdots)}\)が\(\boldsymbol{\theta}\)になります。
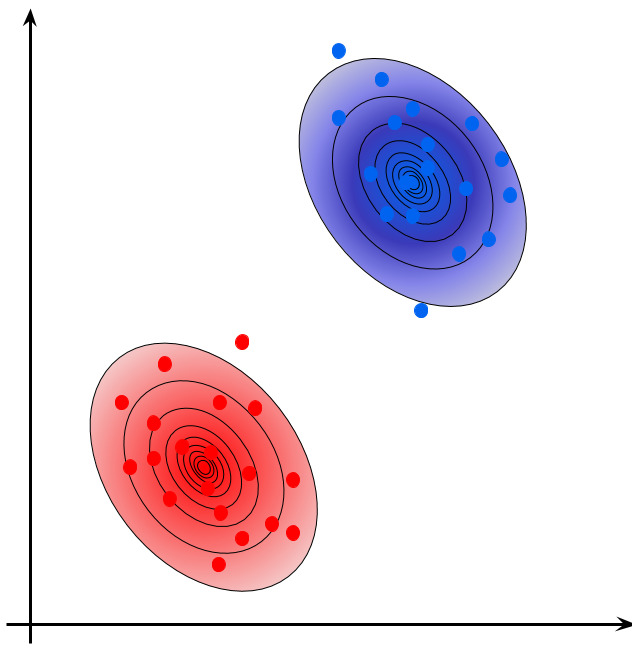
そして、本日の記事の本題であるボルツマンマシンは、条件付確率分布\(p(\boldsymbol{x}|\boldsymbol{\theta})\)にボルツマン分布を仮定します。これが、ボルツマンマシンと呼ばれる所以であり、かつ生成モデルに分類される理由ます。
ちなみに、ボルツマン分布は、機械学習でおなじみのソフトマックス関数と同じ以下の式で表記されます。
$$
p(\boldsymbol{x}|\boldsymbol{\theta}) = \frac{\exp\{-E(\boldsymbol{x}, \boldsymbol{\theta})\}}{Z(\boldsymbol{\theta})}
$$
ボルツマンマシン
ボルツマンマシンについて説明する際に、いきなり定式化するのではなく、ボルツマンマシンとグラフィカルモデルとの関連を説明したあとに、定式化していきたいと思ます。
ボルツマンマシンはグラフィカルモデル
前回、ホップフィールドネットワークについて説明しました。しかし、ホップフィールドネットワークはクロストーク、局所解へ収束という主に2つの課題点がありました。ここでは後者の局所解に収束してしまうことの対処について考えてみたいと思います。局所解に収束する原因への対処は、目的関数の最適化アルゴリズムから多くを学ぶことができます。たとえば、確率的勾配降下法(SGD)はサンプルとランダムに1つ選んできて、それを使ってパラメータを更新します。これは、ランダムに選んできたデータのノイズを使って、局所解から抜け出すことを狙ってのことでした。この確率的な考え方をホップフィールドネットワークにも適用できないでしょうか。
どこに確率性を持たせるかは重要な点で、SGDは、ネットワーク自体は決定論的ですが、学習サンプルをランダムに選ぶことで確率的性質を実現しました。しかし、ホップフィールドネットワークは学習といっても、ヘブ則を使って一瞬で終わります。つまり、学習サンプルを選ぶ動作自体に確率性を持たせることはできません。であれば、ニューロンに確率性を持たせることで局所解から抜け出すことを考える必要がありそうです。そう、これがボルツマンマシンです。え!?ニューロンに確率性を持たせるとグラフィカルモデルと何が関係あるの?っと思うと思います。そこについて説明します。ニューロンの発火の確率はある確率分布に従って選択されますが、その確率分布は最初から決めるわけではありません。つまり、ニューロンの発火の頻度の不確実性の背後にある母集団の確率分布を考えているのです。これは、まさにグラフィカルモデルの考え方であることが納得できると思いますし、生成モデル的アプローチであることに納得いただけると思います。
ボルツマンマシンの定式化
それでは、ボルツマンマシンを定式化していきたいと思います。ホップフィールドネットワークをもとにして定式化する際のポイントは二つあります。
- 決定論的ニューロンを確率的なニューロンに変換すること
- ニューロンの発火に関わる確率分布を最尤推定によって定めること
そして、これらは、ニューロンの発火の確率性に関与するのみで、重みへは影響しません。すなわち、ホップフィールドネットワークと同じくヘブ則を使用して求めます。すなわち、学習は
- ヘブ則により重みを決める
- 最尤推定により確率分布を決める
のステップを繰り返すことで行われます。
ボルツマンマシンの種類
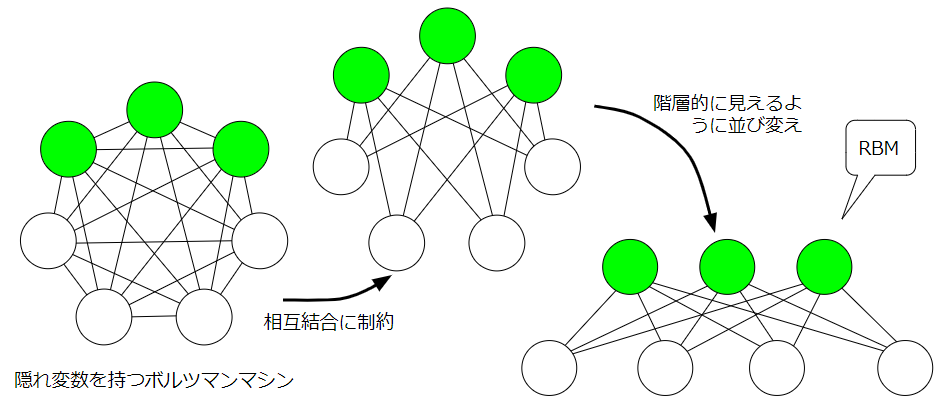
ボルツマンマシンという枠組みでいえばいくつも種類はありますが、まず、隠れ変数の有無により大まかに2つに分けることができます。左のボルツマンマシンは隠れ変数がない、まさにホップフィールドネットワークをグラフィカルモデルにした感じです。右のボルツマンマシンは、可視変数(白)と隠れ変数(緑)からなっています。隠れ変数と可視変数の違いは
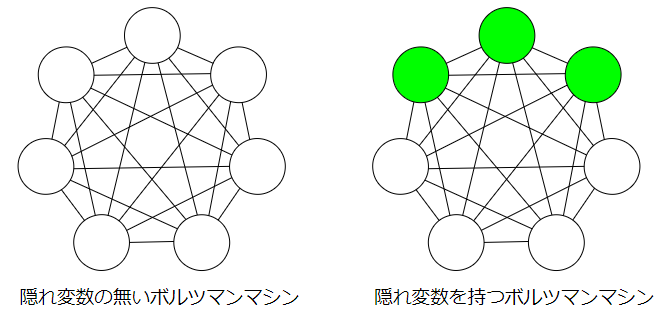
そして、隠れ変数をもつボルツマンマシンに注目したとき、同じ種類の変数間の相互結合に制約を持たせたボルツマンマシンを制約ボルツマンマシン(Restricted Boltzmann Machine;RBM)といいます。図だけ見ると、多層パーセプトロン(Multilayer perceptron;MLP)かぁ~思うかもしれませんが、MLPは有効グラフで決定論的ニューロン、RBMは無効グラフで確率的ニューロンです。RBMの説明は次回の記事に譲り今回は上に示したボルツマンマシンを試したいと思います。
学習と反学習
ボルツマンマシンでは学習と反学習が特徴となります。
隠れユニットの無いBMの対数尤度関数
前回のホップフィールドネットワークの記事と表記を合わせ、記憶パターン数を\(Q\)個とし、\(s\)番目の記憶パターンを行ベクトル\(\boldsymbol{x}^s\)で表すとします。このとき、背後にあるパラメータを\(\phi\)として、条件付確率\(p(\boldsymbol{x}^s|\boldsymbol{\phi})\)を定義し、尤度関数\(L(\boldsymbol{\phi})\)を最大化するように確率分布を学習します。
$$
L(\boldsymbol{\phi}) = \prod_{s=1}^Qp(\boldsymbol{x}^s|\boldsymbol{\phi})
$$
ここで、\(L(\boldsymbol{\phi})\)を最大化することができる\(\boldsymbol{\phi}\)は最尤推定を用いて求めることができます。ちなみに、\(\boldsymbol{\phi}\)はベクトルであることに注意します。
1つのニューロンについて、出力が1となる確率、0となる確率は以下で表されます。
$$\begin{array}{rcl}
p(x_i=1|u_i) & = & \frac{1}{1+e^{-\frac{u_i}{T}}}\\
p(x_i=0|u_i) & = & \frac{e^{-\frac{u_i}{T}}}{1+e^{-\frac{u_i}{T}}}
\end{array}$$
これを全てのニューロンの状態、つまり、あるニューロンは1をとり別のニューロンは0をとり、、、というネットワーク全体としての状態を確率\(p(\boldsymbol{x}^s|\boldsymbol{\phi})\)、より詳しく書けば、
ということになります?!?!?
ネットワークの全ニューロンの状態パターンを行列\(\boldsymbol{x}\)、\(\{w_{ij},\theta_i|0 \leq (i, j) < n\}\)からなる重み、バイアスパラメータ集合を\(\phi\)とすると、エネルギー関数は\(E(\boldsymbol{x}, \boldsymbol{\phi})\)は
$$
E(\boldsymbol{x(t)}, \boldsymbol{\phi}) = -\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^nw_{ij}x_i(t)x_j(t) – \sum_{i=1}^n\theta_ix_i(t)
$$
と書けました。これは、ホップフィールドネットワークのエネルギー関数と同様です。
ここで、ボルツマン分布を考えて、パラメータが\(\boldsymbol{\phi}\)のとき、\(\boldsymbol{x'}\)が生起する確率を
$$
p(\boldsymbol{x'}|\boldsymbol{\phi})) = \frac{\exp\{-E(\boldsymbol{x'}, \boldsymbol{\phi})\}}{\sum_{x_1\in{0,1}}\sum_{x_2\in{0,1}}\cdots\sum_{x_n\in{0,1}}\exp\{-E(\boldsymbol{x}, \boldsymbol{\phi})\}}
$$
と表すことができます。分母の\(\sum_{x_1\in{0,1}}\sum_{x_2\in{0,1}}\cdots\sum_{x_n\in{0,1}}\)は分配関数といわれ(以降、\(\sum_{\boldsymbol{x}}\)と略記)、\(n\)個のニューロンからなるネットワークで取りうることができる全状態のエネルギー関数にマイナスをつけたもののエクスポネンシャルを足しています。したがって、分母に関しては\(\boldsymbol{\phi}\)のみの関数\(Z(\boldsymbol{\phi})\)
$$\begin{array}{rcl}
Z(\boldsymbol{\phi}) & = & \sum_{x_1\in{0,1}}\sum_{x_2\in{0,1}}\cdots\sum_{x_n\in{0,1}}\exp\{-E(\boldsymbol{x}, \boldsymbol{\phi})\}\\
& = & \sum_{\boldsymbol{x}}\exp\{-E(\boldsymbol{x}, \boldsymbol{\phi})\}
\end{array}$$
と置けて、\(\boldsymbol{x'}\)を\(\boldsymbol{x}\)に書き換えて
$$
p(\boldsymbol{x}|\boldsymbol{\phi}) = \frac{\exp\{-E(\boldsymbol{x}, \boldsymbol{\phi})\}}{Z(\boldsymbol{\phi})}
$$
と簡単に表すことが可能になります。これだけ見せられても、ふ~んって感じで実感わかないと思うのでより分かりやすく書いてみます。
$$
\left[\begin{array}{c}
& p(\boldsymbol{x^1}|\boldsymbol{\phi})\\
& p(\boldsymbol{x^2}|\boldsymbol{\phi})\\
& \vdots\\
& p(\boldsymbol{x^Q}|\boldsymbol{\phi})
\end{array}\right]
=
\frac{1}{Z(\boldsymbol{\phi})}
\left[\begin{array}{c}
& \exp\{-E(\boldsymbol{x}^1, \boldsymbol{\phi})\}\\
& \exp\{-E(\boldsymbol{x}^2, \boldsymbol{\phi})\}\\
& \vdots\\
& \exp\{-E(\boldsymbol{x}^Q, \boldsymbol{\phi})\}
\end{array}\right]
$$
これは、重み、バイアスが一意に決定したときの、それぞれのパターンがどのくらいの安定状態なのかを表しています。これらを掛け合わせたものが尤度
$$
L(\boldsymbol{\phi}) = \prod_{s=1}^Qp(\boldsymbol{x}^s|\boldsymbol{\phi})
$$
で、尤度を最大にするとは、記憶させたパターンのそれぞれの安定の程度を掛け合わせたものを最大にするっていうことです。しかし、この状態で微分をするのは難しいので、以下のように対数尤度にします。対数尤度関数にしても性質は変わりません。
$$
\log L(\boldsymbol{\phi}) = \sum_{s=1}^Q \log p(\boldsymbol{x}^s|\boldsymbol{\phi})
$$
隠れユニットの無いBMの対数尤度関数による重み更新の定式化
結論
ボルツマンマシンでは、対数尤度関数を最大化するように重みを更新していきます。そのため、各パラメータに対する対数尤度関数の微分をもとめます。先に、式計算の目標&目的の筋道が分かるように最終的に帰着する部分を示しておきます。
$$\begin{array}{rcl}
\theta_i & \leftarrow & \theta_i + \eta\frac{\partial \log L(\boldsymbol{\phi})}{\partial \theta_i}\\
w_{ij} & \leftarrow & w_{ij} + \eta\frac{\partial \log L(\boldsymbol{\phi})}{\partial w_{ij}}
\end{array}$$
ただし、
$$\begin{array}{rcl}
\frac{\partial \log L(\boldsymbol{\phi})}{\partial \theta_i} & = & \sum_{s=1}^Qx_i^s - Q \mathbb{E}_\boldsymbol{\phi}[x_i]\\
\frac{\partial \log L(\boldsymbol{\phi})}{\partial w_{ij}} & = & \frac{1}{2}\left\{\sum_{s=1}^Qx_i^sx_j^s - Q \mathbb{E}_\boldsymbol{\phi}[x_ix_j]\right\}
\end{array}$$
がここの結論部分になります。重みの更新は勾配上昇法が使用され、更新量は対数尤度関数を使用して求めるということです。このセクションでは、その微分を求める方法を順に示していくことになります。バイアスと重みの更新量の導出方法は同じなので、以下ではバイアスの更新量のみを示していきます。
更新量(対数尤度関数の微分)の導出
先ほど対数尤度関数は
$$
\log L(\boldsymbol{\phi}) = \sum_{s=1}^Q \log p(\boldsymbol{x}^s|\boldsymbol{\phi})
$$
となることを説明しました。右辺の確率\(p(\boldsymbol{x}^s|\boldsymbol{\phi})\)はボルツマン分布
$$
p(\boldsymbol{x}|\boldsymbol{\phi}) = \frac{\exp\{-E(\boldsymbol{x}, \boldsymbol{\phi})\}}{Z(\boldsymbol{\phi})}
$$
を代入することで、
$$\
\log L(\boldsymbol{\phi}) = \sum_{s=1}^Q \{-E(\boldsymbol{x}^s, \boldsymbol{\phi}) - \log Z(\boldsymbol{\phi})\}
$$
と表すことができます。これより、
$$\begin{array}{rcl}
\frac{\partial \log L(\boldsymbol{\phi})}{\partial \theta_i} & = & \frac{\partial}{\partial \theta_i}
\left\{
-\sum_{s=1}^QE(\boldsymbol{x}^s, \boldsymbol{\phi})
\right\}+\frac{\partial}{\partial \theta_i}
\left\{
Q\{-\log Z(\boldsymbol{\phi})\}
\right\}\\
&=& A + B
\end{array}$$
となります。ここでは、便宜的に2つの項を順番に\(A\)と\(B\)で置きました。
では、順番に求めていきます。
$$\begin{array}{rcl}
A & = & \frac{\partial}{\partial \theta_i}\left\{-\sum_{s=1}^QE(\boldsymbol{x}^s, \boldsymbol{\phi})\right\}\\
&=& \frac{\partial}{\partial \theta_i}\sum_{s=1}^Q\left\{\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^nw_{ij}x_i^sx_j^s + \sum_{i=1}^n\theta_ix_i^s\right\}\\
&=& \frac{\partial}{\partial\theta_i}\sum_{s=1}^Q\sum_i^s\\
&=& \sum_{s=1}^Qx_i^s
\end{array}$$
$$\begin{array}{rcl}
B & = & \frac{\partial}{\partial \theta_i}Q\{-\log Z(\boldsymbol{\phi})\}\\
&=& -Q\frac{1}{Z(\boldsymbol{\phi})}\frac{\partial}{\partial \theta_i}Z(\boldsymbol{\phi})\\
&=& -Q\frac{1}{Z(\boldsymbol{\phi})}\frac{\partial}{\partial \theta_i}\left\{\sum_\boldsymbol{x}\exp\{-E(\boldsymbol{x}, \boldsymbol{\phi})\}\right\}\\
&=& -Q\frac{1}{Z(\boldsymbol{\phi})}\frac{\partial}{\partial \theta_i}\left\{\sum_\boldsymbol{x}\exp\{\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^nw_{ij}x_ix_j + \sum_{i=1}^n\theta_ix_i\}\right\}\\
&=& -Q\frac{1}{Z(\boldsymbol{\phi})}\sum_\boldsymbol{x}x_i\exp\{\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^nw_{ij}x_ix_j + \sum_{i=1}^n\theta_ix_i\}\\
&=& -Q\frac{1}{Z(\boldsymbol{\phi})}\sum_\boldsymbol{x}x_i\exp\{-E(\boldsymbol{x}^s, \boldsymbol{\phi})\}\\
&=& -Q\sum_\boldsymbol{x}x_i\frac{\exp\{-E(\boldsymbol{x}^s, \boldsymbol{\phi})\}}{Z(\boldsymbol{\phi})}\\
&=& -Q\mathbb{E}_\boldsymbol{\phi}[x_i]
\end{array}$$
したがって、
$$\begin{array}{rcl}
\frac{\partial \log L(\boldsymbol{\phi})}{\partial \theta_i} & = & A + B\\
&=&\sum_{s=1}^Qx_i^s - Q\mathbb{E}_\boldsymbol{\phi}[x_i]
\end{array}$$
となります。同様の手順で\(\frac{\partial \log L(\boldsymbol{\phi})}{\partial w_{ij}}\)についても導けるます。
勾配の計算量について
先ほど、勾配を定式化しましたが、ここには大きな問題点があります。それはユニットが増えると組み合わせが爆発的に増えるため、計算が現実的でなくなる点です。より丁寧に説明すると、分配関数\(\sum_boldsymbol{x}\)の部分の計算量が、ニューロン数を\(n\)として\(2^n\)となる点が問題です。ニューロン数が増えるごとに、計算量が指数関数的に増えるため、大規模なものになると実現できてはなくなります。そのため、様々な近似方法が提案されています。なかでも、次回の制約ボルツマンマシンの回で説明しますが、コントラスティブダイバージェンスが有名です。
隠れユニットの無いBMの一連のプロセス
ここまで、隠れユニットの無いボルツマンマシンについて、確率的ニューロンと重み更新の定式化について説明してきました。ここでは、それら一連のプロセスを再確認します。
基本的には以下のループです。
- 時刻\(t\)の状態\(s_t\)から、次状態\(s_{t+1}\)へ遷移
- 重みを更新する
この際、1ではアニーリング法により出力が確率的に変化する確率的ニューロンを1つ選び、ホップフィールドネットワークと同様の計算を行い、確率的に出力を決定します。2では、1の結果をから対数尤度案数が最適化されるように重みを更新します(勾配上昇法)。
隠れユニットがあるBMの場合
ここまでのまとめ
ボルツマン分布から見るソフトマックス関数の解釈
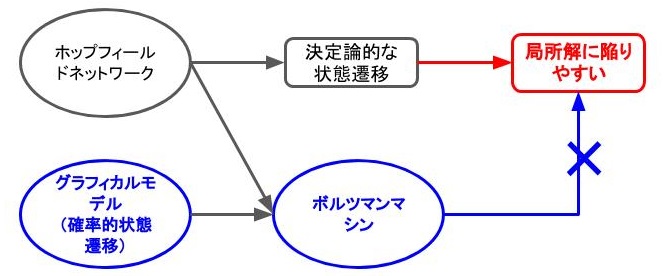
時刻\(t\)のネットワークの状態を\(s_t\)とします。このとき、ホップフィールドネットワークは\(s_t\)から\(s_{t+1}\)へ決定論的に遷移しますが、ボルツマンマシンは、確率的に遷移します。これにより、局所解に陥りやすいという問題を緩和することができました。
ボルツマンマシンは、ホップフィールドネットワークの一種と解釈することができる一方で、注意すべき点もあります。それは、ホップフィールドネットワークは脳の情報処理からヒントをえており、モデルは海馬で学習方法はヘブ則を使用していますが、ボルツマンマシンは、グラフィカルモデルから派生しているため、ネットワークの最適化方法は生物学的妥当性のない勾配降下法になっているところです。
局所解に陥りにくいとはどういうことか
ごめんなさい、間に合いませんでした。。。後で追加できればと思います。
ボルツマンマシンを試す
ごめんなさい、間に合いませんでした。。。後で追加できればと思います。
