今まで再帰型ニューラルネットワークのプログラミングはあまりしたことがなく、理解が浅いので、しっかりと理解し使えるようになるために、今回から数回は再帰型ニューラルネットワークの勉強をしていくことにしました。では、今回は単純再帰型ニューラルネットワーク(SimpleRNN)を使用して正弦波を学習させてたいと思います。
必要なライブラリをインポートします。今回はPandasを使用しませんが、今後使用する可能性もあるため、インポートしておきました。
#import the NumPy, Pandas and Matplotlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#import these classies below
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.layers.recurrent import SimpleRNN
from keras.optimizers import Adam
from keras.callbacks import EarlyStopping学習データの準備
まずは、語句の定義をしておきます。本記事では、
・学習データ:学習したい時系列データ全体(ex:sin, 日経平均株価)
・系列データ:学習データをモデルに入力するフォーマットに変換したもの
この使い分けが正しいかは確認ができませんでした... 今回の記事では個の使い方で統一させていただきます。学習データは正弦波(sin)に雑音を加えたものとします。下記のコードでは、大きさが-0.1から0.1の範囲のノイズを正弦波に加える操作を行っています。数値yは配列データであり、グラフ化すると図1のようになっています。
np.random.seed(0)
def make_sin(x, amp, T=100):
noise = amp * np.random.randint(-10, 10, len(x))
return np.sin(2*np.pi*x / T) + noise
x = np.arange(200)
y = make_sin(x, 0.01)array([ 0.02 , 0.11279052, 0.02533323, 0.11738131, 0.17868989,
0.27901699, 0.35812455, 0.51577929, 0.56175367, 0.47582679,
・
・
・
-0.68778525, -0.52582679, -0.50175367, -0.42577929, -0.35812455,
-0.35901699, -0.19868989, -0.20738131, -0.20533323, 0.02720948])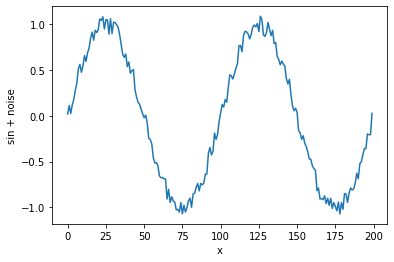
系列データセットの生成
先ほど準備した学習データから、再帰型ニューラルネットワークが学習できる入力データへフォーマット(系列データ)を変更していきます。再帰型ニューラルネットワークを学習するとき、無限範囲で学習が行えればベストですが、BPTTの計算の都合((巣籠悠輔『詳解ディープラーニング TensorFlow・Kerasによる時系列データ処理』マイナビ, 2017, p.218))から、出力へ影響を与えることができる範囲を決める必要があります。以下のプログラムでは、過去25個までのデータを考慮して次の出力を決定することになります。具体的には、i(>=25)においてy[i-25: i]をモデルに入力し、y[i]を学習する問題になります。これを、スライドさせ、系列データとして格納していきます。このとき、targetの対応するインデックスにはy[i]を格納していきます。
l = 25
def make_dataset(y, l):
data = []
target = []
for i in range(len(y)-l):
data.append(y[i:i+l])
target.append(y[i + l])
return(data, target)
(data, target) = make_dataset(y, l)
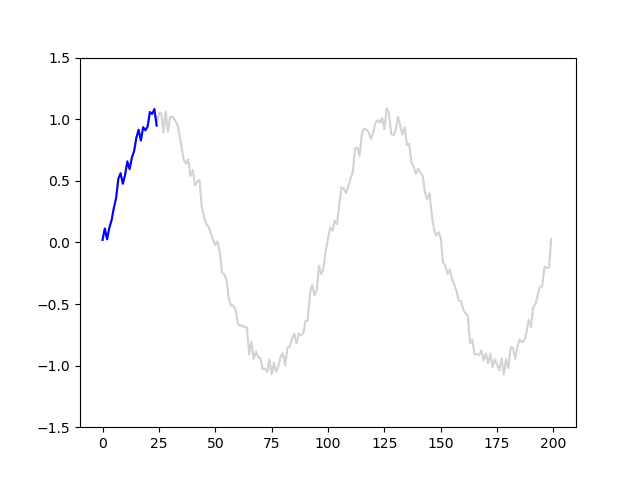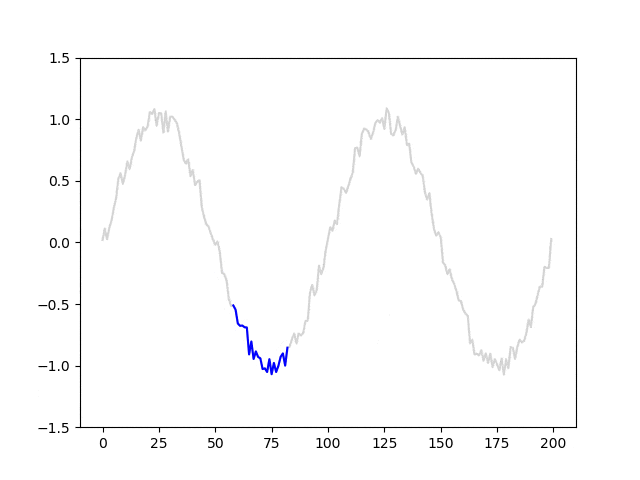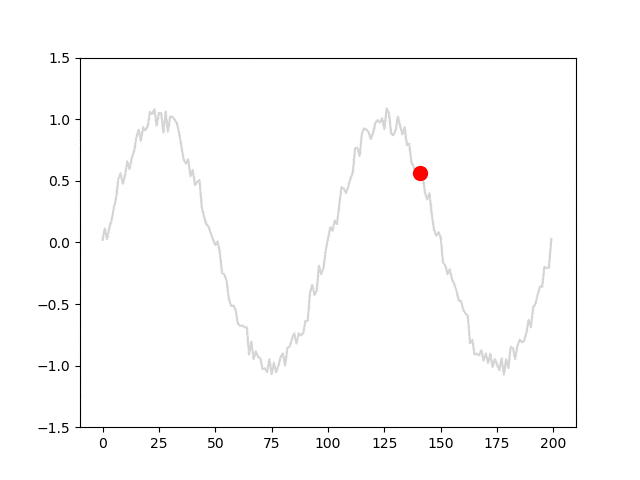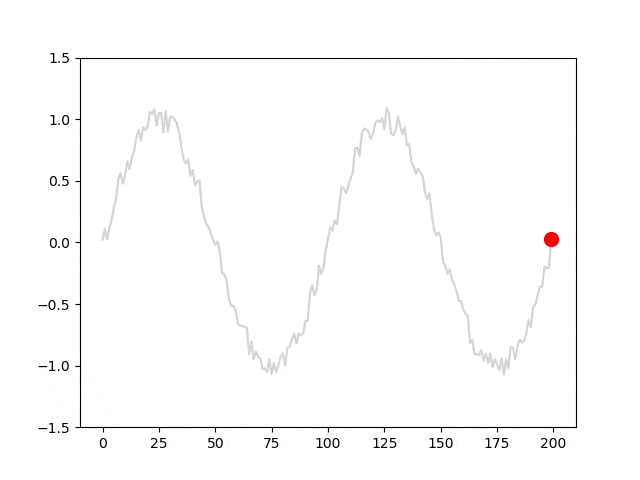
data = np.array(data).reshape(-1, l, 1)モデルに入力される系列データと教師信号の移り変わりが分かりやすくなるように、アニメーションを作成しました。青線はl=25における系列データを、赤丸は対応する教師信号を表しています。
モデルを定義する
それではモデルを定義していきたいと思います。今回は、入力層、再帰層、出力層の3層で、入力層及び出力層のニューロン数は1個、再帰層のニューロン数は200個です。(一見すると、3層ニューラルネットワークのように感じますが、時間的な次元で深層になっています。)
入力層から再帰層(再帰部分を含む)まではSimpleRNNクラスにより1行で定義します。再帰層の活性化関数はデフォルトでtanhになっています。再帰層(再帰部分を含まない)から出力層までは、DenseとActivationの2行で定義しています。出力層は重回帰分析なため、誤差関数には平均二乗誤差を使用します。early_stoppingは訓練中にfitメソッドからコールバックして使用するために定義しています。これにより、学習の進み具合に応じて、全てのエポックを行うか打ち切るか判断されます。
num_neurons = 1
n_hidden = 200
model = Sequential()
model.add(SimpleRNN(n_hidden, batch_input_shape=(None, l, num_neurons), return_sequences=False))
model.add(Dense(num_neurons))
model.add(Activation('linear'))
optimizer = Adam(lr = 0.001)
model.compile(loss="mean_squared_error", optimizer=optimizer)
early_stopping = EarlyStopping(monitor='val_loss', mode='auto', patience=20)学習させる
モデルを学習させます。学習するにあたり、バッチサイズは300、エポックは100にしました。
model.fit(data, target, batch_size=300, epochs=100, validation_split=0.1, callbacks=[early_stopping])引数についての補足
- validation_split:交差検証を行うにあたり、検証用データに使用される割合を設定します。大きさは0~1の間です。
- callbacks:callbacksは与えられた学習過程で適応される関数の集合で、今回の例では、early_stoppingが毎回適応しています。
学習データを再現させる
系列データに使用した範囲を正しく再現できているか確認してみます。入力データは学習時に使用した系列データです。
pred = model.predict(data)この予測結果predをグラフに描画してみます。
plt.figure(figsize=(15, 4))
plt.subplot(1, 3, 1)
plt.plot(x, y, color='blue')
plt.xlabel('x')
plt.ylabel('sin + noise')
plt.subplot(1, 3, 2)
plt.xlim(-10, 210)
plt.plot(x[25:], pred, color='red')
plt.xlabel('x')
plt.ylabel('pred')
plt.subplot(1, 3, 3)
plt.plot(x, y, color='blue', label='sin+noise')
plt.plot(x[l:], pred, color='red', label='pred')
plt.xlabel('x')
plt.legend(loc='lower left')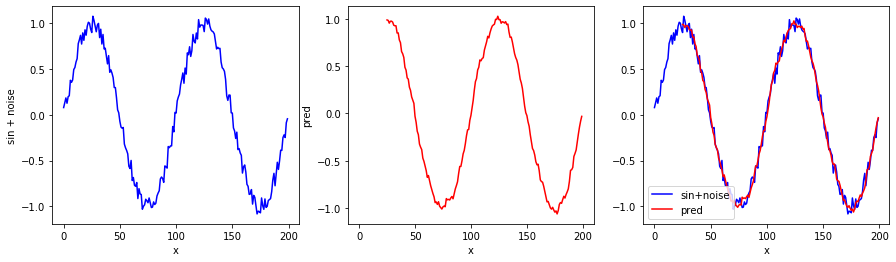
図3において、左の青色グラフは学習対象のグラフ(sin + noise)、真ん中の赤色グラフはモデルが学習データを入力として受けた時のグラフ、右は二つを合成したものです。学習データについては、正しく学習ができたようです(後に説明しますが、学習データが再現できただけで、未来予測ができるほど学習ができたと断定することはできません)。
未来を予測させる
未来を予測させる場合、先ほどとは入力データが少し異なります。つまり、先ほどは入力データに自身の出力は含まれませんでしたが、今回は自身の出力が含まれます。そのため、自身の予測結果を利用して更に予測を行います。
start = data[-1].reshape(1, l)[0]
for i in range(800):
predicted = model.predict(start[-l:].reshape(1, l, 1))
start = np.append(start, predicted)
pred_y = np.append(y, start[l:])
plt.xlim(-10, 1010)
x_ = np.arange(200, 1000)
plt.plot(x, y, color='blue', label='sin+noise')
plt.plot(x_, start[l:], color='red', label='predicted')
plt.legend(loc='upper right', ncol=2)
plt.ylim(-1.5, 1.5)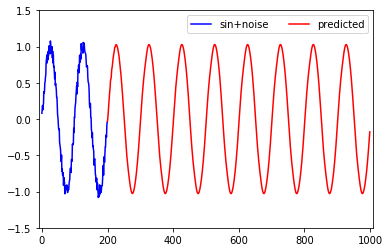
結果のグラフを見る限りは、振幅と周期共にnoiseが取り除かれた正しい正弦波が学習されたと考えることができます。
SimpleRNNへ入力する系列データの長さlを変えてみる
上の例では入力する系列データの長さlを25としました。では、長さを変えた時にどのような変化をするのか気になったので実験してみました。実験するにあたり、描画をする関数を作成しました。
"""
Lはリストで、例えば系列データの長さをl=1,2,3と実験したい場合は
L=[1, 2, 3]としてLを受け渡す。widthとheightはsubplotをするときに、
plt.subplot(width, height, 番号)で使用する。以下のプログラムでは、
1つの学習結果について、2つのグラフを出力するため、表示する
グラフの数は学習したモデルの数の倍になる。ちなみに、以下の関数
では、毎回modelを使用しているため、グラフを表示することのみに
使用した後、残らない。
"""
def rnn_test(L, width, height, n_hidden=200):
num_neurons = 1
plt.figure(figsize=(20, 20))
for i, l in enumerate(L):
(data, target) = make_dataset(y, l)
data = np.array(data).reshape(-1, l, 1)
model = Sequential()
model.add(SimpleRNN(n_hidden, batch_input_shape=(None, l, num_neurons), return_sequences=False))
model.add(Dense(num_neurons))
model.add(Activation('linear'))
optimizer = Adam(lr = 0.001)
model.compile(loss="mean_squared_error", optimizer=optimizer)
early_stopping = EarlyStopping(monitor='val_loss', mode='auto', patience=20)
model.fit(data, target, batch_size=300, epochs=100, validation_split=0.1, callbacks=[early_stopping])
pred = model.predict(data)
start = data[-1].reshape(1, l)[0]
for _ in range(800):
predicted = model.predict(start[-l:].reshape(1, l, 1))
start = np.append(start, predicted)
pred_y = np.append(y, start[l:])
plt.subplot(width, height, 2*i+1)
plt.title("l={}".format(l))
plt.xlim(-10, 210)
plt.plot(x[l:], pred, color='red')
plt.xlabel('x')
plt.ylabel('pred')
plt.subplot(width, height, 2*i+2)
plt.xlim(-10, 1010)
x_ = np.arange(200, 1000)
plt.plot(x, y, color='blue', label='sin+noise')
plt.plot(x_, start[l:], color='red', label='predicted')
plt.legend(loc='upper right', ncol=2)
plt.ylim(-1.5, 1.5)
plt.show()
L=[1, 2, 4, 8, 16, 32, 64, 128]
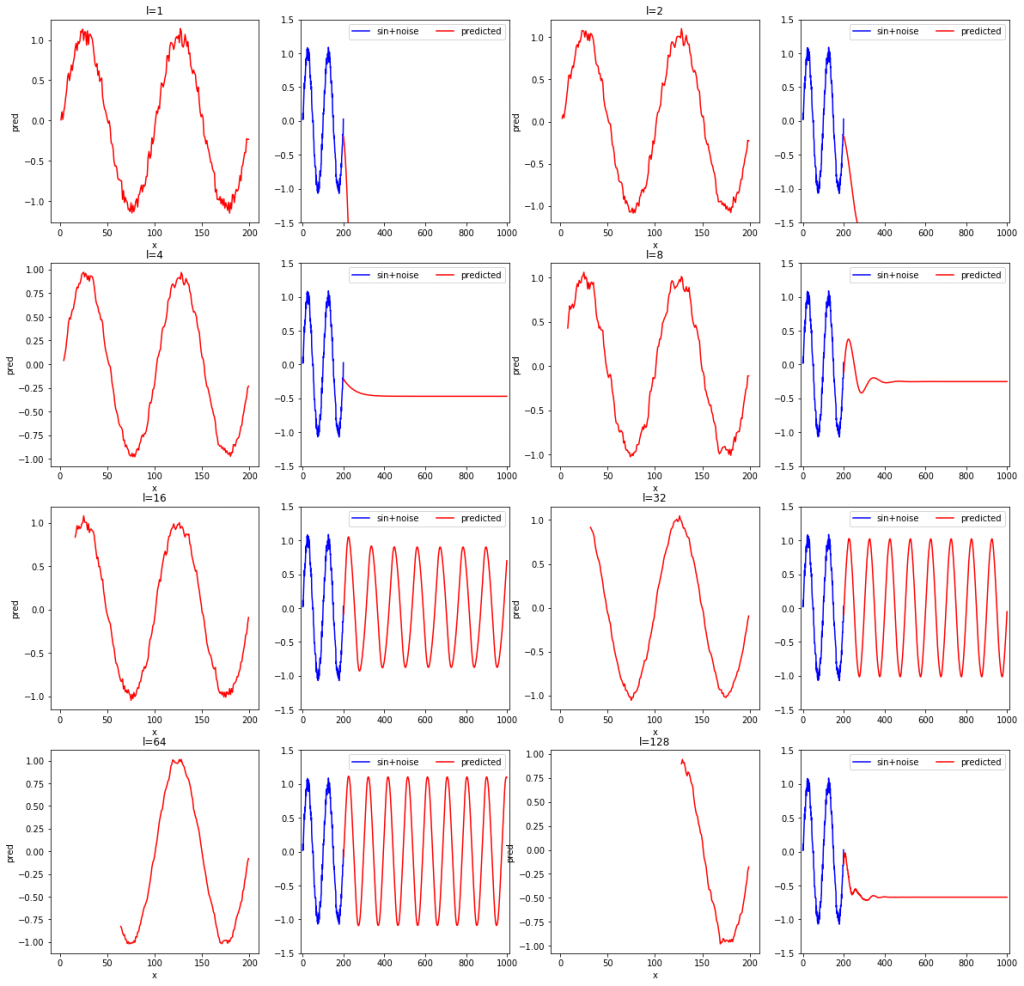
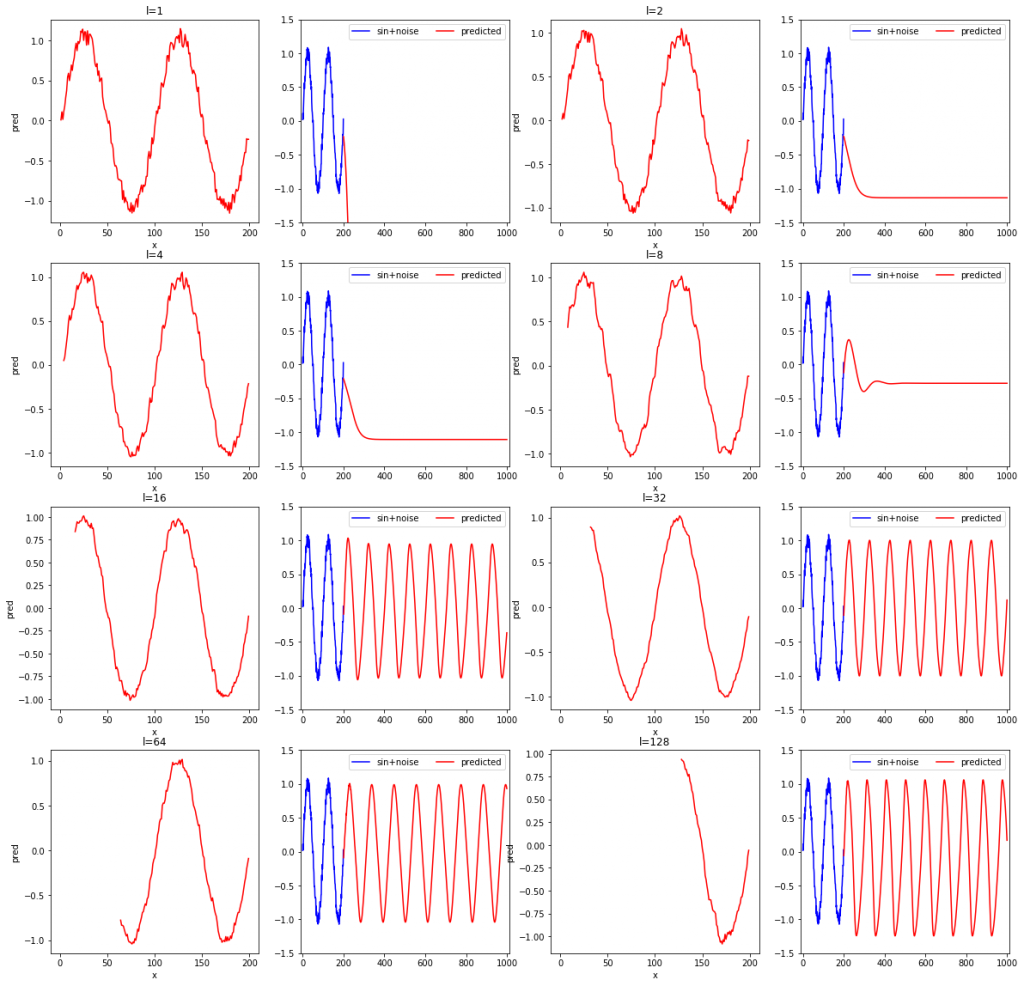
rnn_test(L, width=4, height=4)l=1, 2, 4, 8, 16, 32, 64, 128と変化させながら、確かめてみました。各系列データの長さに対して、2枚ずつ結果のグラフが出力されます。2枚のグラフのうち、左は学習データの再現結果を、右は未来の予測結果です。SimpleRNNやDenseクラスで重みを初期化するときにランダム値が使用されており、モデルを定義する度に重みの初期値が異なるため、3回実行してみます。
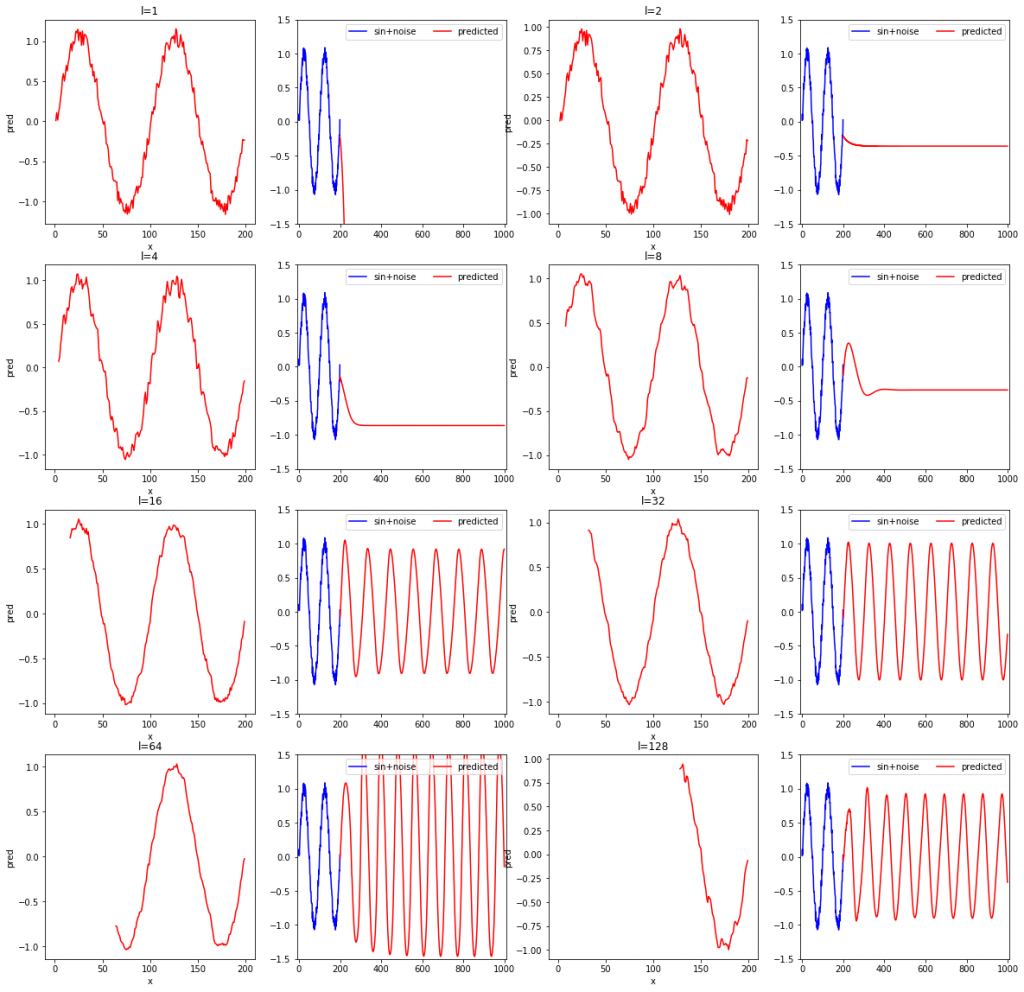
また、他にl=2, 4, 6, 8, 10, 20, 30, 40と変化させた場合についても実験したので示しておきます。
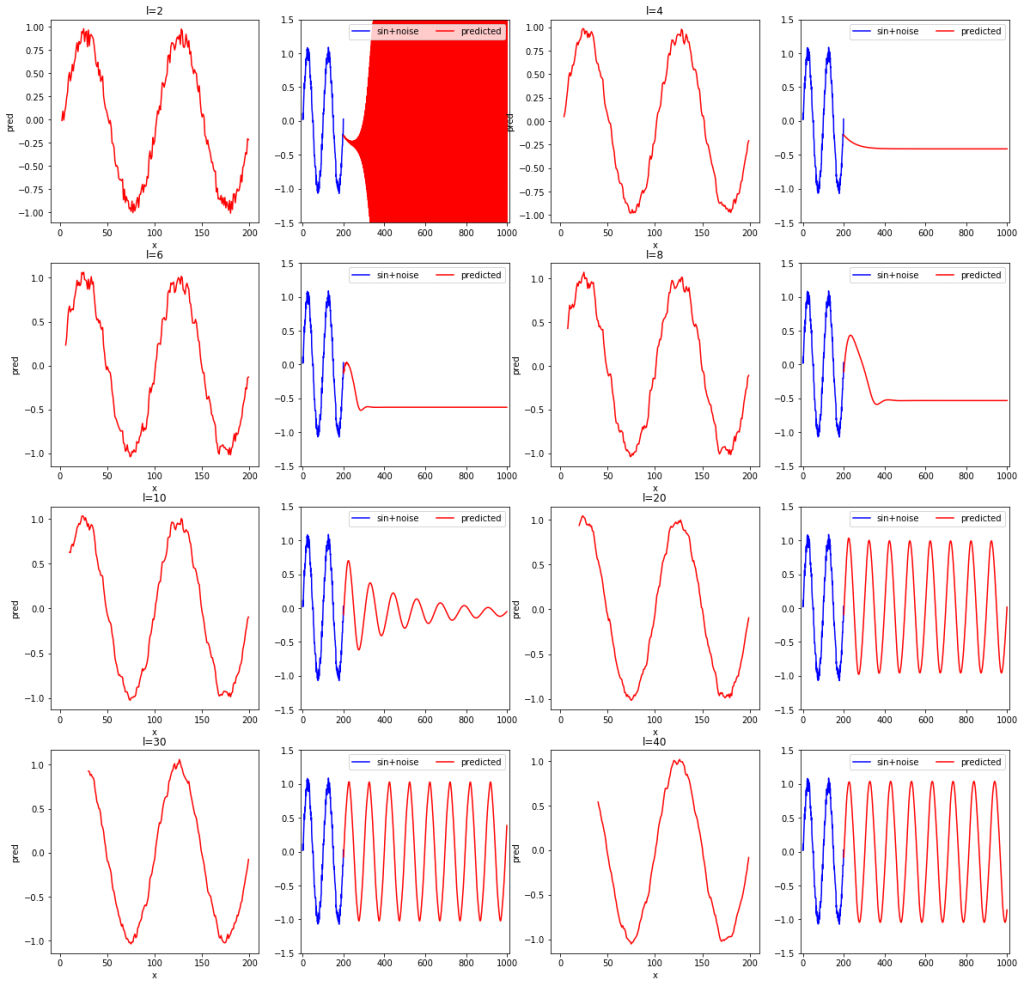
グラフを見て読み取れることを箇条書きで示します。自分一人で考えたものになるため、他の人が見れば別の気付きがあると思います。
- 学習データの再現性(各左側のグラフ)に限定すれば、lが短くても問題なく、lが短いほど学習データのノイズまで忠実に再現している。
- 系列データの長さが短いと場合によっては発散する。
- 上記の結果おいて3回とも未来予測が安定しているのはl=16と32だった。
- 学習データを滑らかに再現できるほど、つまり、再現結果にノイズが少ないほど、安定して未来予測ができている(l=32より)。
- 学習データが再現できても未来予測ができるかは関係がない。
- 再現したものにノイズが含まれないモデルほど未来を予測するのに適した傾向がある。
しかし、これには疑問点もあり、それについての私の考えを示します。
- 系列データの長さを長くすると、短い場合より学習に使用できる系列データ数が少なくなるため、同じく比較していいのか。
→学習データが固定な場合、系列データの長さlと系列データの数はトレードオフな関係になるため、今回の正弦波の場合はl=32がちょうどつりあっていたのではないか。そのため、系列データの数が同じ状態で比較をした場合、系列データの長さが長くても問題ないと考えられる。
次に、学習に使用しているsin+noise波の周期は100であることから、l=100にしたらどうかという疑問を持ったため実験してみました。
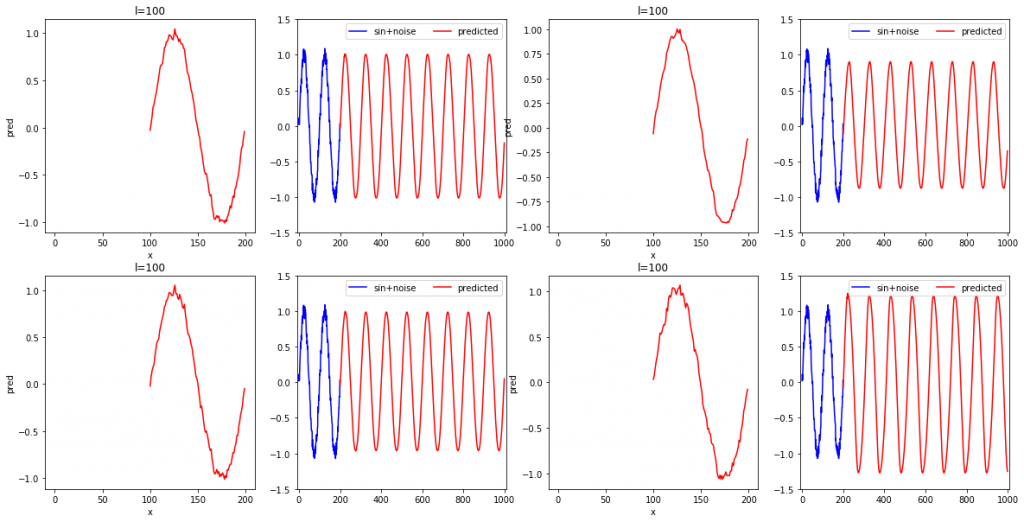
再現性については、思った以上にノイズを含んでいることが分かりました。未来予測については、振幅の大きさがうまく学習できていないことがあるようです。これは、系列データの数が短い場合よりも少ないことに起因しているかもしれません。それを次のセクションで確かめていきたいと思います。
ちなみに、l=25の場合を4回繰り返した時の結果は以下のようになります。
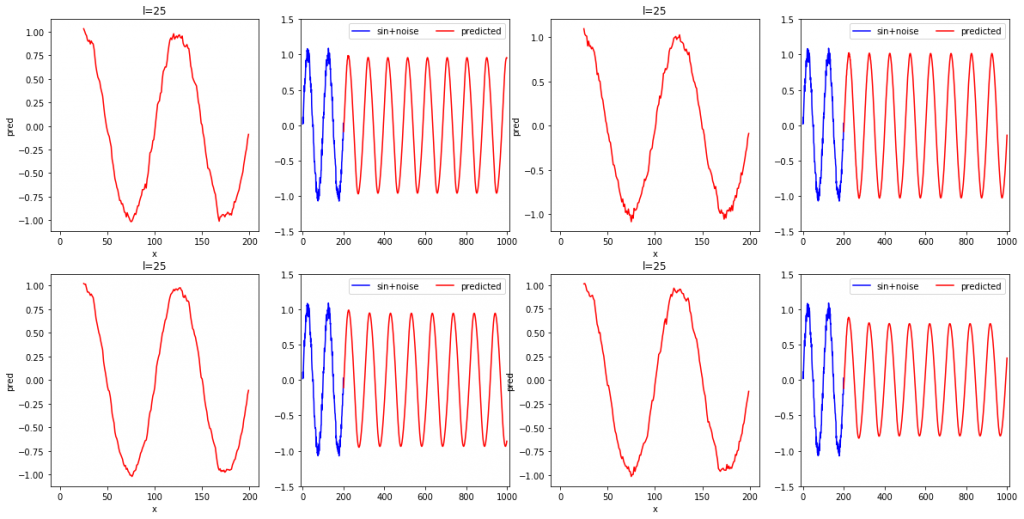
l=32を4回繰り返した場合は以下のようになりました。
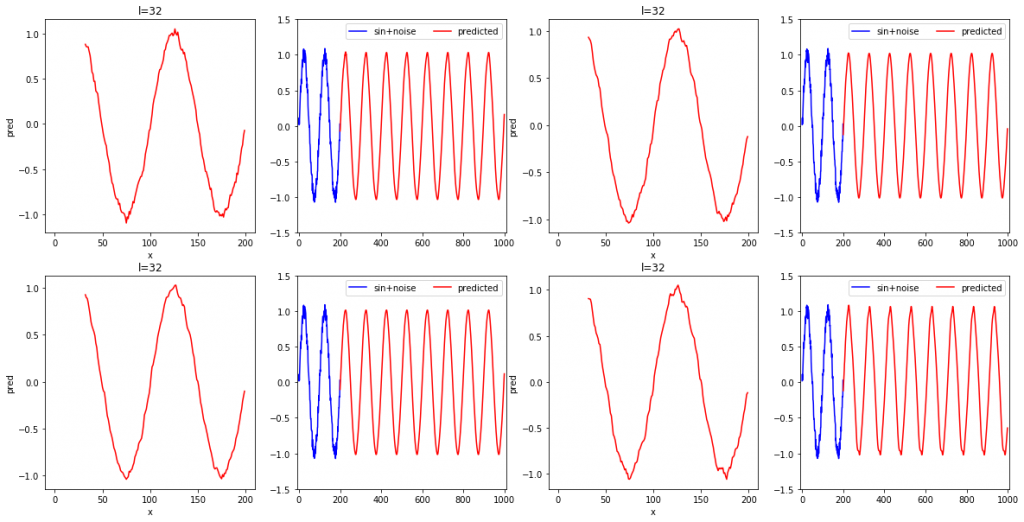
l=32の場合は、4回に渡り高精度で再現ができました。一方で、l=25の時は振幅がうまく学習できていない場合が多々見られました。
学習データを長くして系列データの長さを長くした場合を確かめる
思い切って学習データを長くし、系列データの数を増やしました。
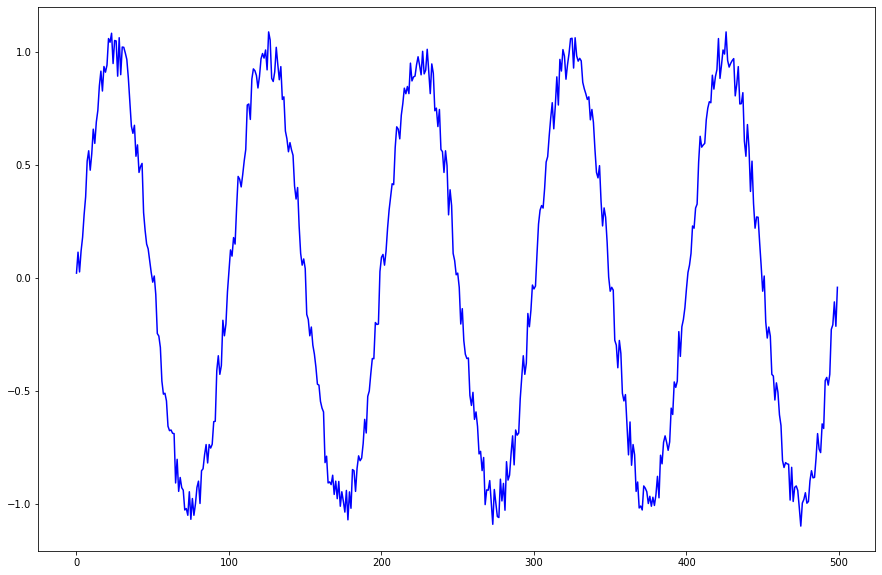
上記のsin+noise波をl=100のモデルで学習させたときの4回分の結果を以下に示します。
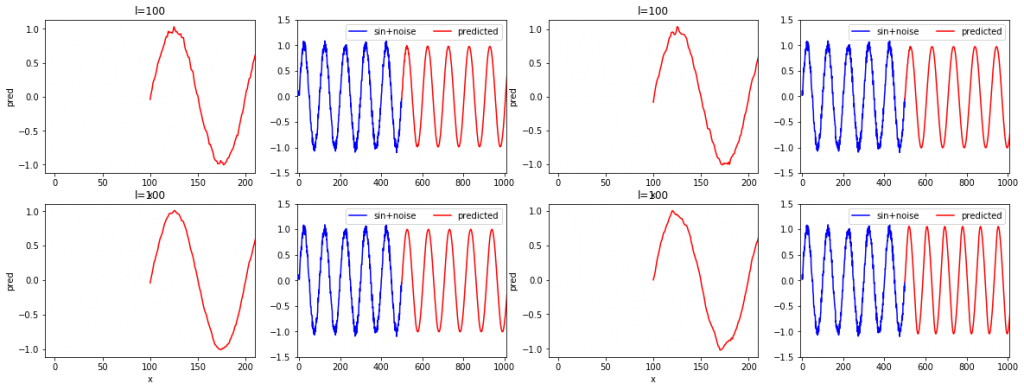
先ほどの結果では、4回中1~2回は再現性の欠ける出力がされていましたが、系列データ数が多くすることで、4回とも正しく再現できているため、しっかりとしたモデルを構築できる確率が上がったと予想できます。
まとめ
系列データの長さが短すぎると、未来予測を上手くできませんが、系列データが長い分には学習性能が悪くなるとは言えず、一つ言えるとすれば、BPTTに必要な計算コストが増えてしまう欠点があるくらいと思われます。しかし、これが通用するのは、限りなく長い学習データが入手出来る場合であり、実際に入手できるものは有限です。そのため、系列データの長さと系列データの数はトレードオフな関係になり、系列データの長さを単に長くすればよいわけではなくなります。結果、様々な長さの系列データでモデルを学習させ、性能と計算コスト共に良い長さlを見つけることが、良いモデルを構築する一つのカギになるでしょう。
