Word2VecとEmbedding層について考察してみた

Word2VecやEmbedding層について自身の理解が曖昧だったので、学習がてら自身の考察を示しながらまとめました。

分散表現

名前など物理的な計測が不可能な記号集合をベクトルに対応付けたものを分散表現（distributed representation）といいます。この変換操作は、トークンをベクトル空間に埋め込む操作であることから埋め込み（embedding）ともいわれます（一般的に自然言語処理の分野でトークンは単語であるため、単語埋め込み（word embedding）と呼ぶことが多い）。

Word2Vec

Word2Vecとは、WordをVectorに変換するという意味で分散表現そのものを指すと解釈できますが、より狭義でCBOWやSkip-gramの2つのモデルを指すのが一般的です。勉強会等で登壇者の説明を聞いたり自身が説明したりするときはWord2Vecが分散表現そのものを指しているのか、CBOWとSkip-gramのみを指しているのか注意する必要があります。

CBOWやSkip-gramというモデルは学習を通じて以下で説明する分散表現を習得します。具体的に

"King"-"Man"="Queen"-"Woman"

というベクトル計算が可能な分散表現です。これは数百次元と高次元ベクトルの演算であるため、King、Man、Queen、Womanの関係に注目して主成分分析等により2次元に次元削減すると、以下ような構造が得られます。

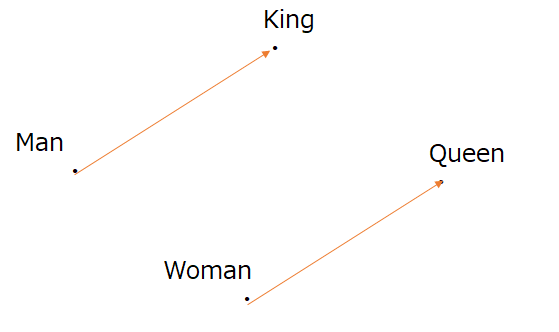
ここから、"Woman"から"Queen"という単語を得たければ、"Woman"に"King"-"Man"で表されるベクトルを足せばいいということになります。

Embedding層

任意のトークンに対応する数値番号（つまり、スカラー量）を入力として受け、密なベクトル空間に埋め込む操作を実現する層です。内部のアーキテクチャとしては入力された番号のインデックス部分のみが1である疎なOneHotベクトルをそれより低次な密ベクトルに線形写像しており、計算過程でOneHotなベクトル表現にする操作をワンクッション置いていますが、層をブラックボックスとして、入力と出力のみに注目すれば、単語同士の意味関係を表さない記号空間（入力）をベクトル空間（出力）に埋め込んでおり、まさに分散表現の定義そのものを表す層です。

そもそもEmbeddingとは何か

先ほど分散表現とWord2Vecについて説明した要領で十分な部分もありますが、この手の説明ではWord2VecとしてCBOWやSkip-gramれ触れつつも、いきなりEmbedding層が登場してくる書籍が多い印象で、Embedding層による分散表現＝Word2Vecなる分散表現と自身が勘違いしていたため、必ずしもEmbedding層による分散表現＝Word2Vecなる分散表現ではないことを敢えて説明したくてこのセクションを用意しました。

次のセクションで説明するニューラルネットに繋げることができる端的な説明をなかなか見つけられなかったのですが、いい感じな解説を見つけたので一部を以下に引用しました。

Naturally, every feed-forward neural network that takes words from a vocabulary as input and embeds them as vectors into a lower dimensional space, which it then fine-tunes through back-propagation, necessarily yields word embeddings as the weights of the first layer, which is usually referred to as Embedding Layer.

https://goo.gl/ojJjiE

これによれば、単語を表すベクトルをそれよりも低次元空間に写像する順伝播型ニューラルネットワークはEmbedding層だというのです。すなわち、やってることはDense層と変わらない（もちろんEmbedding層の入力形式はスカラーでDense層の入力形式はベクトルという点は異なる）と言っているわけです。より厳密にいうと、Dense層はバイアスを含んでいるため、線形写像というよりはアフィン写像をしていることも異なります。すなわち、Dense層において全てのバイアスを0にして、かつ活性化関数を恒等関数するという特別な場合がEmbedding層といえそうです。

では、なぜEmbedding層を使うのかという疑問が生まれます。自身の憶測では、分散表現の定義そのものを表すのがEmbedding層であり、明示的に層の役割を定めることで、使用性や移植性・利便性が上がるためと考えます。また、Embedding層は使用頻度的にも多いので、毎回Dense層を使用してEmbedding層を定義しなおしていては大変だからと考えられます。

Embedding層で得られる分散表現

内容的には前のセクションで説明したことと少し重複しますが重ねて説明します。まず、Word2Vecは分散表現の中でもCBOWやSkip-gramを使用したときに得られる特別な場合であり、Embedding層で獲得できるであろう全ての分散表現＝Word2Vecとは限りません。そのため、Embedding層を使えば必ずWord2Vec表現が得られるという理解は間違っています。Embedding層が学習後にWord2Vecなる分散表現を表現できるのは、CBOWやSkip-gramを構築して学習させたときのみです。でも、Embedding層が使われるのは、自然言語処理の面で使用しやすく、また、Skip-gramですでに学習した重み行列を移植することも可能であるからといえます。では、Word2VecのようにCBOWやSkip-gramで得られる分散表現以外の表現は意味をなさないかといえばそうではありません。逆に、まっさらなEmbedding層を毎回使用することで、所望のタスクに特化した分散表現が得られることも多いと考えられます。

埋め込み行列と埋め込みベクトル

それでは、次で具体的なEmbedding層の実現方法を示していきたいと思います。

Embedding層の内部アーキテクチャは、大きく2つに分けられ、1つ目は入力記号を示す数値をOneHotベクトルに変換すること、2つ目はそのOneHotベクトルをより低次のベクトル空間上に線形写像することです。前者は特に説明するまでもないので、後者の部分について説明します。

線形写像なので、変換行列\(W_{embedding}^T\)を考えます。vocabulary_size（以下:n）は入力することができるトークンの種類、一般的には単語の種類に対応し、embedding_size（以下:m）は埋め込み次元のサイズを示します。

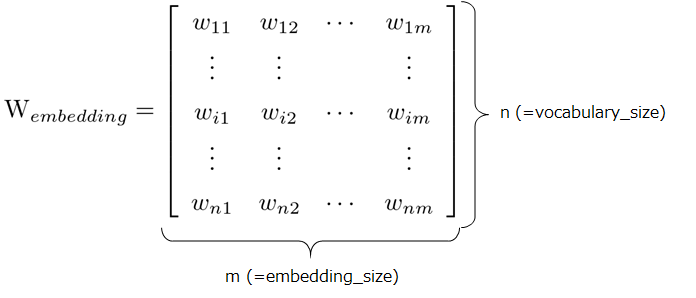
このとき、OneHotベクトルから、埋め込み次元へは以下のようにして変換することができます。

この重み行列はニューラルネットを構成するニューロン同士の辺の重みに対応することから、Embedding層は、以下のような図で表すアーキテクチャで実現できることになります。重み行列の学習はBP（誤差逆伝播）により行われます。例えば単語のweatherに対応する数値が256とします。このとき、256をEmbedding層に入力すると、256番目のみが1のOneHotベクトルが生成され、変換行列により埋め込み行列に写像されたものが出力されるステップを表しています。

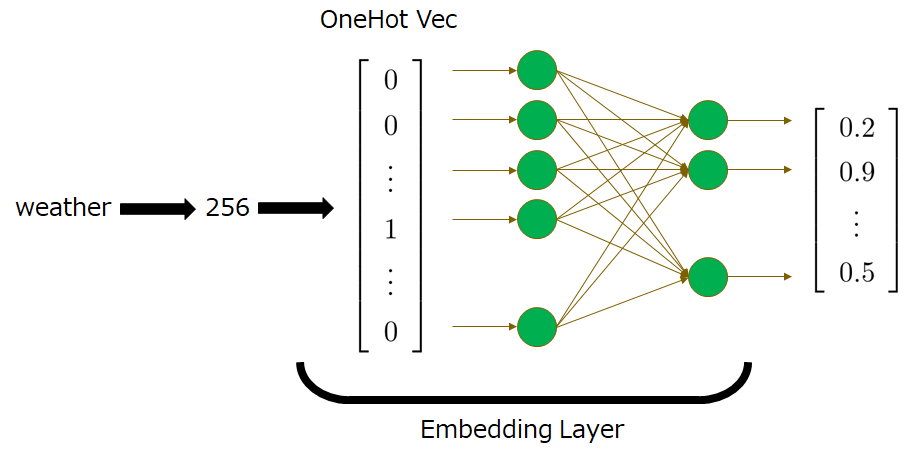
そして、学習で得られた行列から、記号の番号を\(num\)として\(W_{embedding}[num]\)のように埋め込みベクトルを取得できます。このような性質よりEmbedding層は、ルックアップテーブルもしくは辞書と説明されることがあります。

各ライブラリでEmbedding層を使用する方法

TensorFlowのembedding _lookup

※現在はplaceholderが無効になっていますが、有効な場合の表記を示しました。

voc_size = 5000
emb_size = 100

# 変換行列W_{embedding}をパラメータで定義
params = tf.Variable(tf.random_uniform([voc_size, emb_size], -1.0, 1.0))

# スカラーの番号が任意のバッチサイズで入力される状況を仮定
ids = tf.placeholder(tf.int32, shape=[None])

tf.nn.embedding_lookup(
        params=params,     # 変換行列
        ids=ids    # 入力形式を定義
)

kerasのEmbedding

voc_size = 5000
emb_size = 100

# TensorFlowとは異なり外部で変換行列を定義する必要はないが、
# 引数として変換行列の形態、パラメータの初期化方法等を指定する必要がある
Embedding(input_dim=voc_size,     # vocabulary_size
          output_dim=emb_size,     # embedding_size
          embeddings_initializer='uniform', 
          embeddings_regularizer=None, 
          activity_regularizer=None, 
          embeddings_constraint=None, 
          mask_zero=False, 
          input_length=None)

PyTorchのEmbedding

# これは引数情報を含んでいるので、このままターミナルに
# コピペすれば動くというわけではないですが、Kerasと
# 基本的には変わらないため、引数情報のみ示します
Embedding(num_embeddings: int, 
          embedding_dim: int, 
          padding_idx: Optional[int] = None, 
          max_norm: Optional[float] = None, 
          norm_type: float = 2.0, 
          scale_grad_by_freq: bool = False, 
          sparse: bool = False, 
          _weight: Optional[torch.Tensor] = None)

まとめ

Embedding層は、物理的計測の不可能な記号集合をベクトル空間に写像する分散表現そのものの定義を実現するもので、COWやSkip-gramを使えば単語同士の意味によるベクトル計算が可能な分散表現を得ることができます。それ以外の分散表現も学習可能で、それぞれのタスクに特化して埋め込みを学習することで、言語のような物理的計測が不可能な記号集合とニューラルネットワークのかけ橋として重要な役割を担っていると考えられます。