本記事では、ロボットのアームの制御などでも使用されるRRT(Rapidly-exploring Random Tree)について、概要とアルゴリズム、そして実際にプログラムコードを動することろまで解説します。
要点
RRT(Rapidly-exploring Random Tree)とは、高速な探索をするランダムツリーです。具体的には、移動ロボットの現在位置から目標位置に行くまでのパスを障害物を考慮してルート探索を行うタスクや、ロボットアームの現在の先端位置から目標の先端位置へ移動させる軌道を計算するタスクなどで使用されます。名前にある通り探索はランダムに進められるのが特徴です。適用先は高次元空間であることが多々あるにもかかわらず、高速に実現できるのがこのアルゴリズムの特徴です。一方で欠点もあり、それはランダム故、探索結果の最適性は保証されないところです。この課題を解決するために様々な手法が提案されています。
RRTのアルゴリズム
基本的に、経路探索や軌道生成のような問題では木を広げていくことでゴールにたどり着こうとします。何も手がかりがないので、探索空間内をランダムにサンプリングし、それをもとに木を広げていくアイディアは割と思いつく人はいるのではないかと思います。これがRRTのアルゴリズムです。RRTのアルゴリズムを以下に示します。
- 処理(1):グラフ\(G=(V, E)=(\{x_{init}\}, \emptyset)\)で初期化
- 処理(2):\(n\)回反復処理
- 処理(2-1):探索空間内の1点\(x_{rand}\)をサンプリング
- 処理(2-2):\(x_{rand}\)に最も近いグラフ\(G\)上の点(\(x_{nearest}\in V\))を計算
- 処理(2-3):\(x_{nearest}\)から\(x_{rand}\)を結んだ線上の\(x_{nearest}\)から指定の距離のところを表す点\(x_{new}\)を計算
- 処理(2-4):\(x_{new}\)がグラフ\(G\)のノード\(V\)に存在せず、かつ、\(x_{new}\)と\(x_{nearest}\)の間に障害物がないことをチェック
- 処理(3):ゴールに辿り着いたか確認
- 処理(4):\(x_{init}\)から\(x_{goal}\)までのパスを計算
処理(1)の詳細
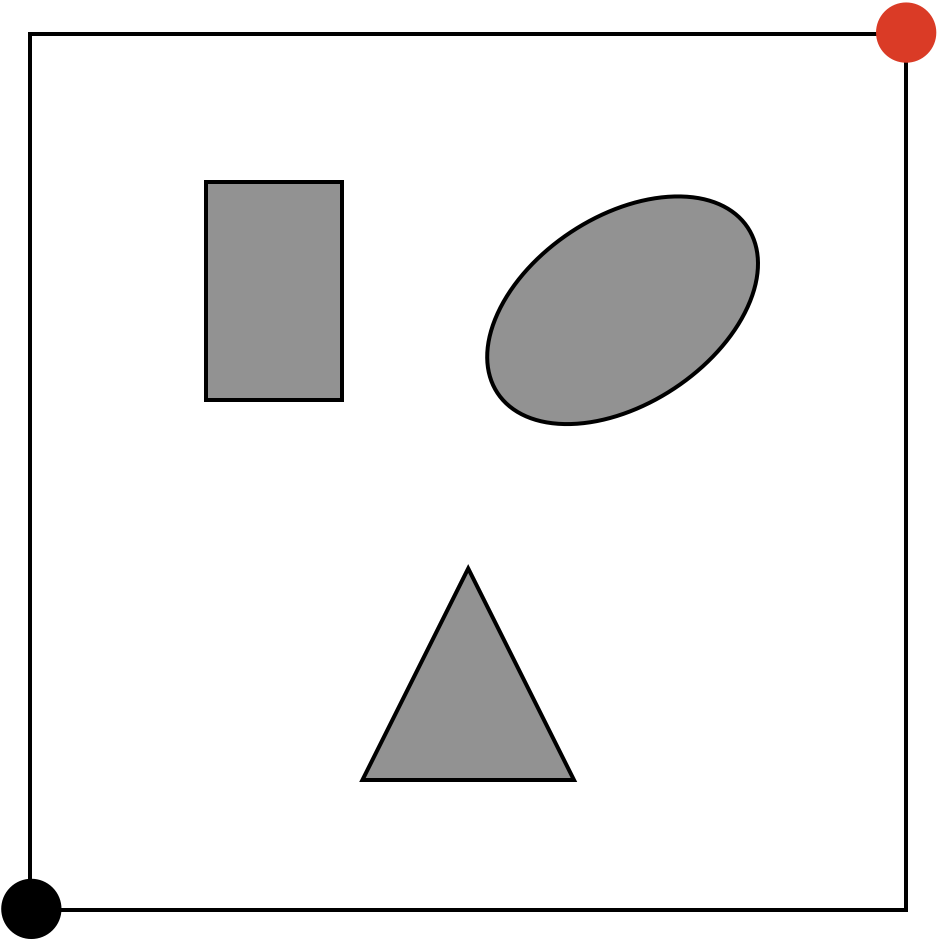
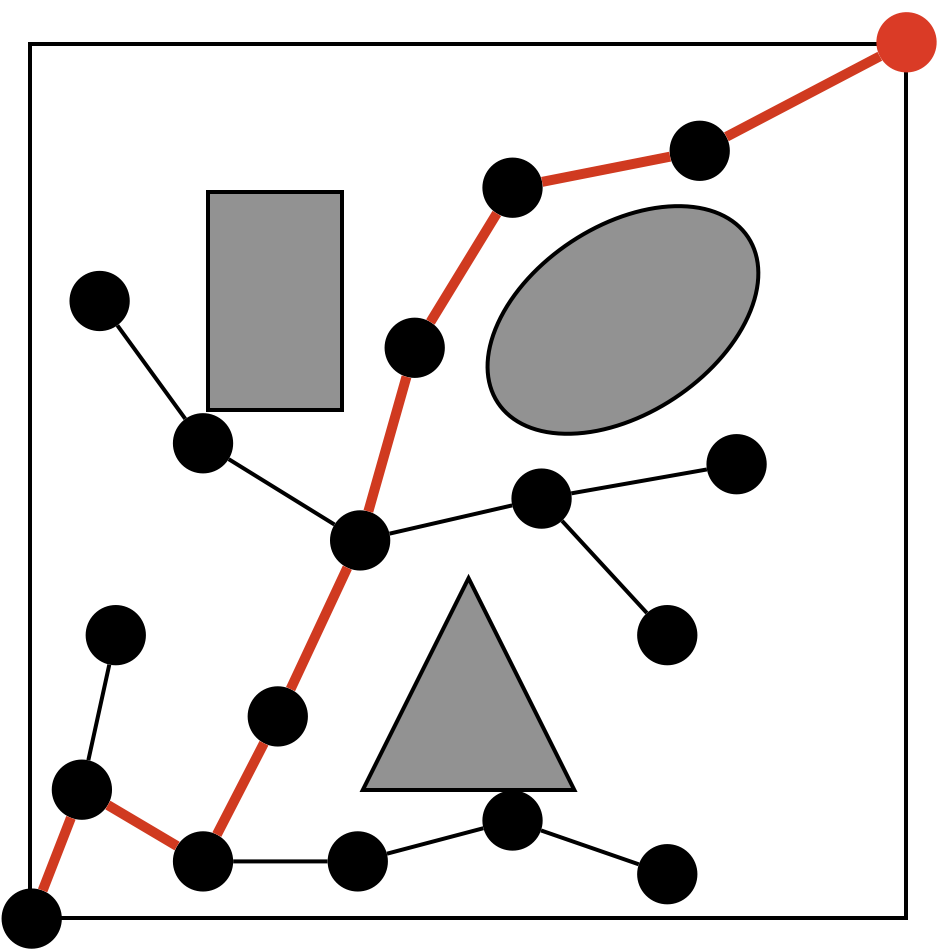
処理(1)ではグラフ\(G\)を初期化します。その際、ノード集合\(V\)はスタート地点を表すノード\(x_{init}\)のみ、辺集合\(E\)は空集合に初期化されます。以降では、理解しやすくするために具体例を考えていきます。具体例として、周囲の正方形の黒枠の中に長方形と楕円形、三角形の障害物がある探索空間(白色部分)を考えてみます。右上の赤点が記載されてるところがゴール地点とします。処理(1)を行うと、スタート地点を表すノード(今回は左下の点)のみを持つグラフとして初期化されます。
処理(2-1)の詳細
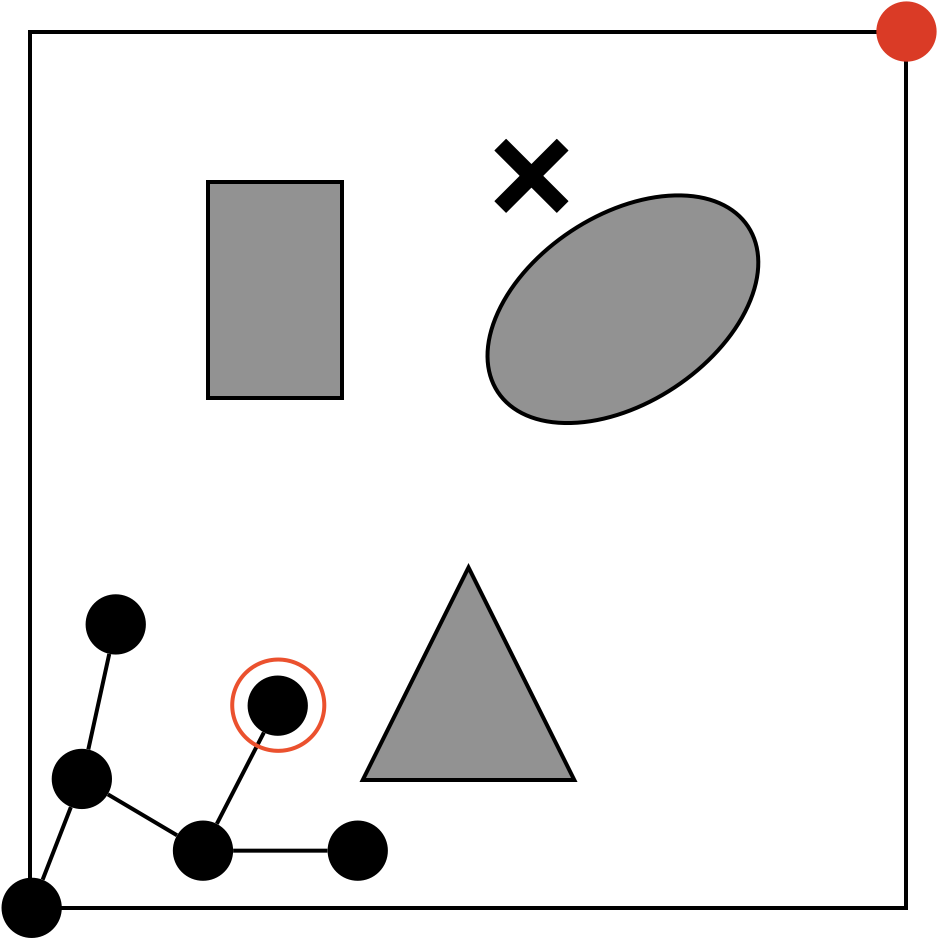
処理(2-1)から処理(2-4)は繰り返し行うので、ここでは任意の状態(下)を考えたいと思います。これは何回か探索が行われた後の状態です。
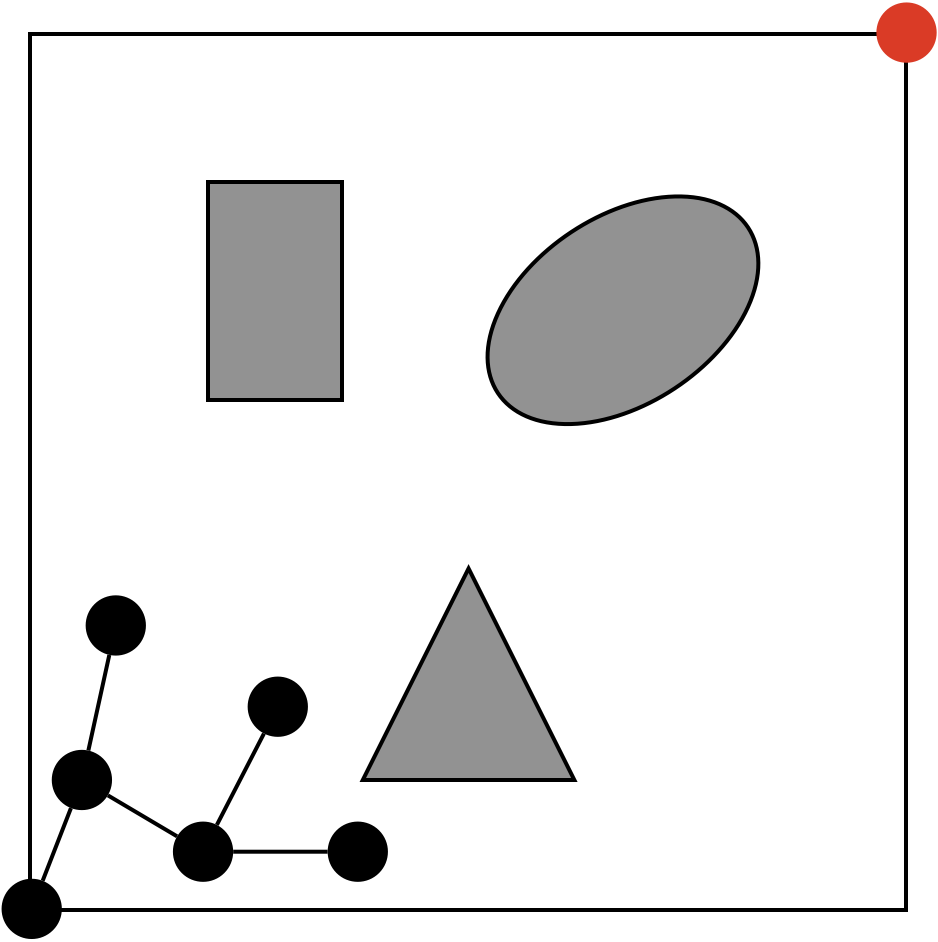
ここで、探索空間(白色の領域)から一箇所をランダムにサンプリングし、得られた点\(x_{rand}\)が図中の✕部分とします。
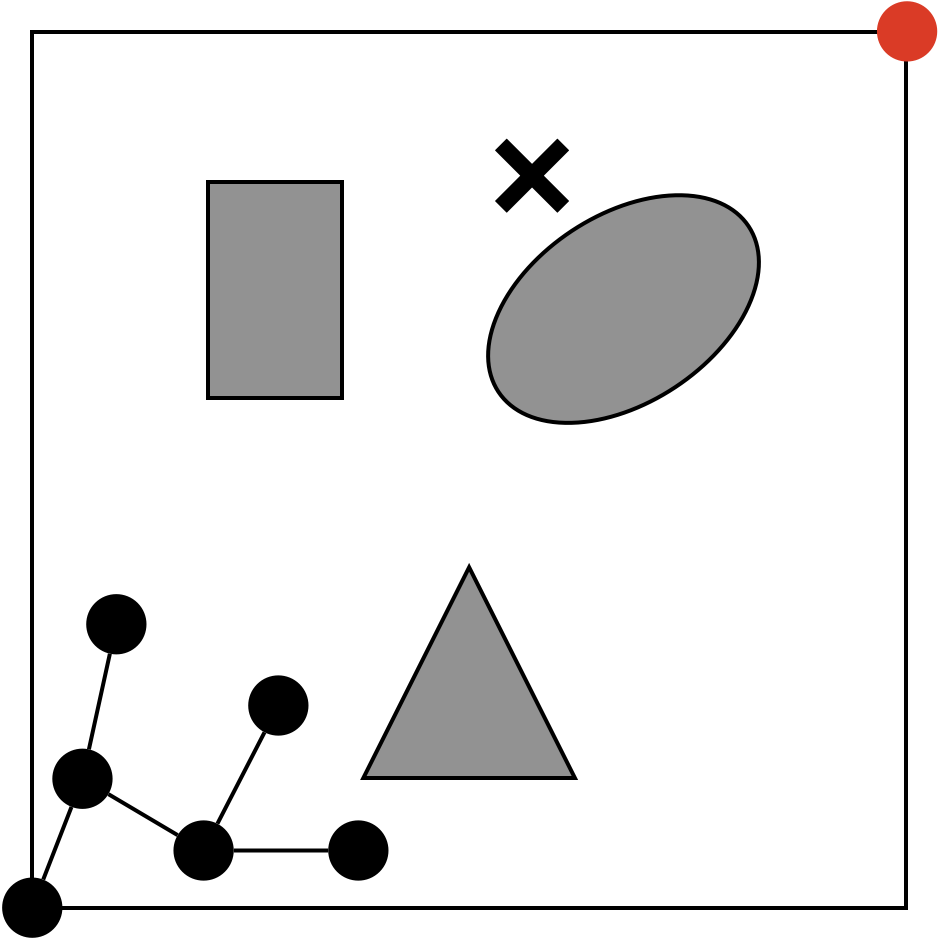
処理(2-2)の詳細
処理(2-2)では、処理(2-1)でランダムに選んだ点に最も近いグラフG上のノードを選びます。今回の例では赤丸で囲った点です。
処理(2-3)の詳細
処理(2-3)では、処理(2-1)でランダムにサンプリングした点(✕)と、処理(2-2)で選んだ最短ノードを線で結んだとき、グラフ側の点から既定の長さだけ離れた位置に新しく点を付与します。
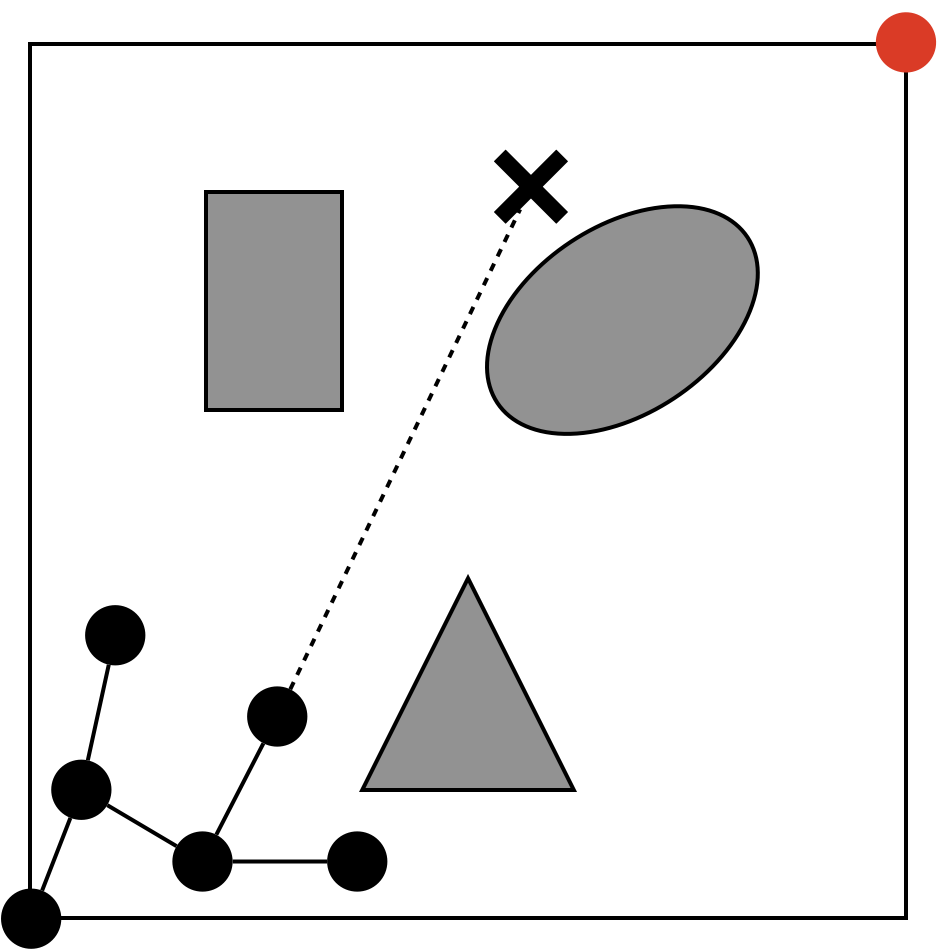
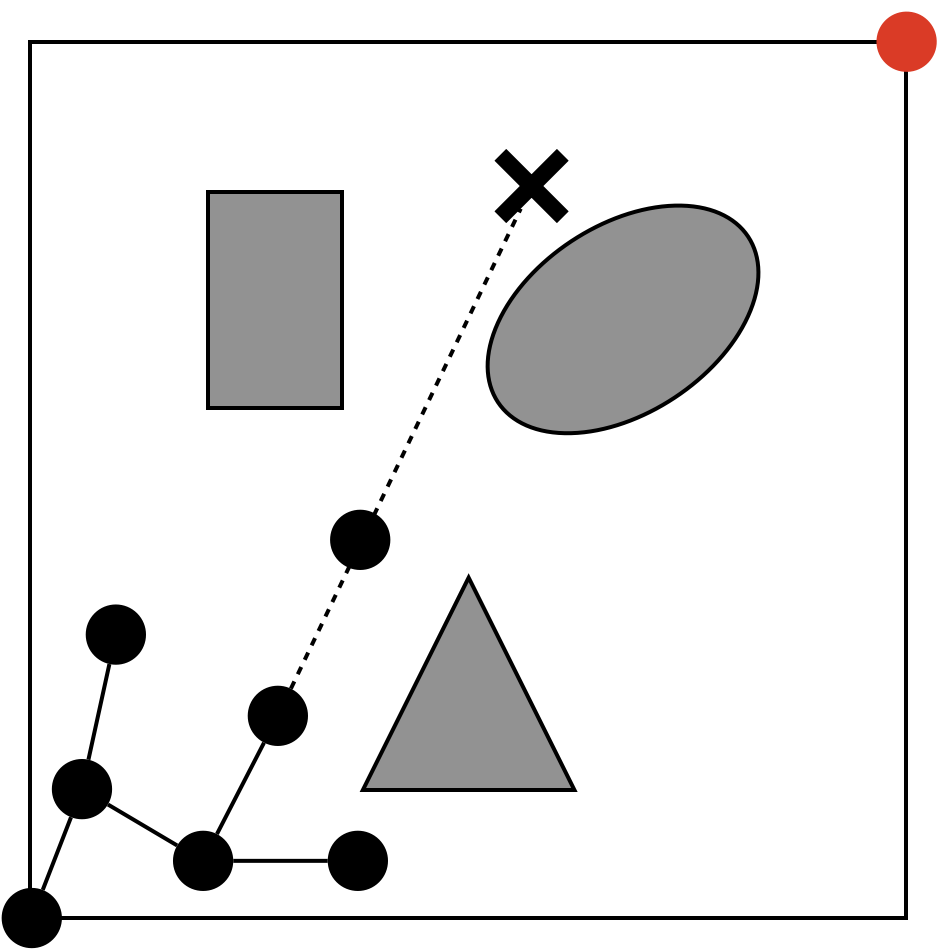
パスプランニングでは、ちゃんと移動できるようなパスを出力する必要があり、ランダムサンプリングした点\(x_{rand}\)を直接、フラフのノードとして追加してしまうと、パスとしては不自然になってしまうため、既に決められた間隔ごとにノードを追加していきます。そのための作業です。
処理(2-4)の詳細
処理(2-4)では、処理(2-3)で選んだ点がグラフを構成するノードに含まれていないことと、障害物と交差していないことを確認し、これらに問題がなければ、新たにグラフを構成するノードとして追加(\(V\leftarrow V \cup \{x_{new}\}\))し、エッジを付与(\(E \leftarrow E \cup \{(x_{nearest}, x_{new})\}\))します。
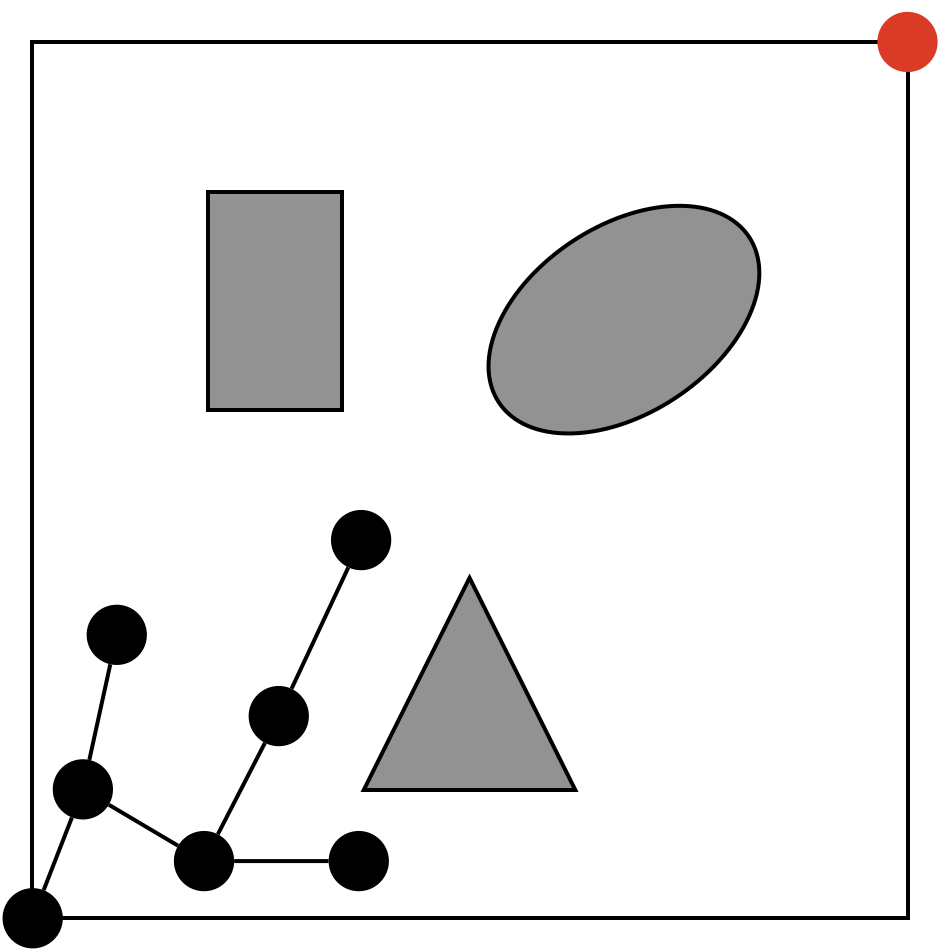
処理(3)の詳細
処理(3)では、処理(2-1)から(2-4)までを指定回数\(n\)だけ反復したあとの木がゴールに到達したかを確認します。到達できた場合は、「成功」、到達できなかった場合は「失敗」です
実は、このプロセスは処理(2-5)として反復処理に含まれることがあり、その場合は、\(n\)回の反復処理をすべて実行する前にゴールへ到達したかどうかを察知できるため、時間の短縮に繋げることができます。
処理(4)の詳細
ゴールへ到達できた場合は、スタート地点からゴール地点を結ぶルートを計算し返します。
ここまでの流れを1つの図にすると以下のようになります。
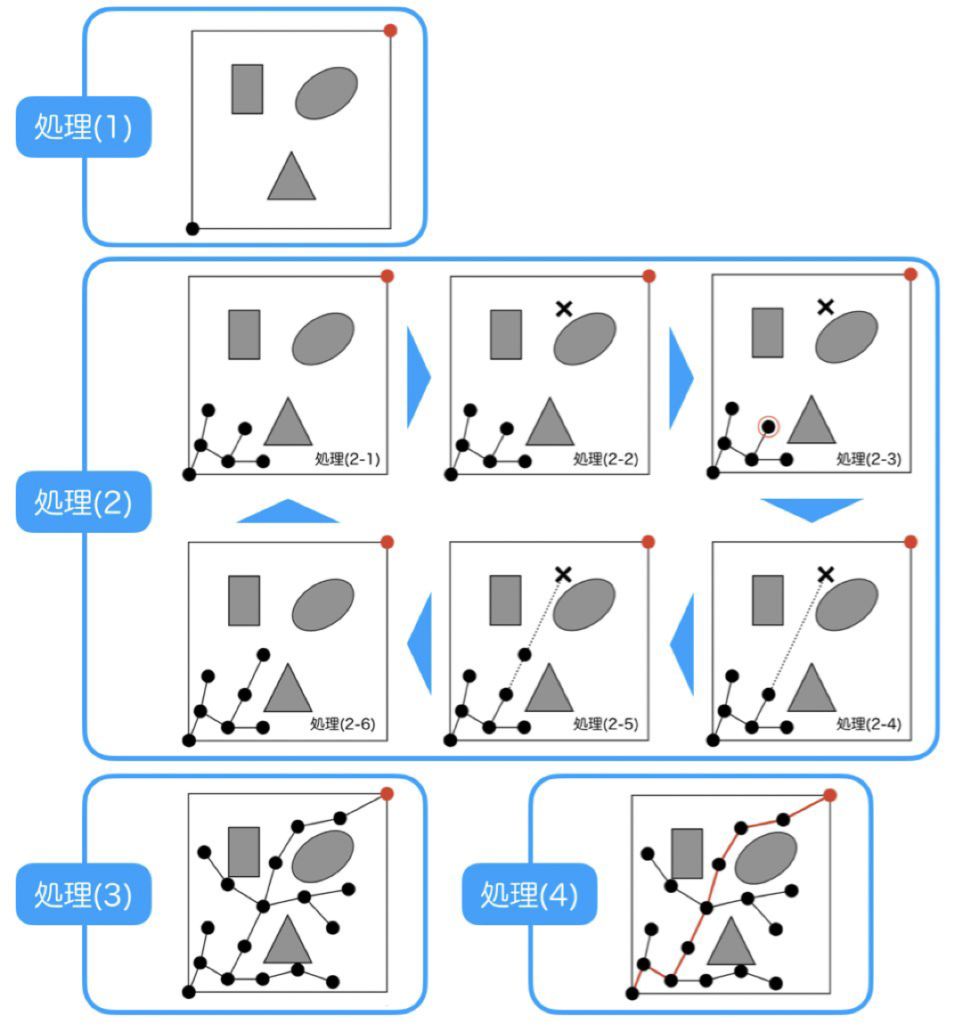
簡単に説明すると、処理(1)でグラフを初期化、処理(2)でランダムサンプリングを使って木を大きく、処理(3)でゴールへの到達確認、処理(4)でゴールに到達していた場合はパスを返す、という感じになります。
プログラムで試す
RTTを触ってみようと思って調べると、以下のリポジトリがヒットしました。MITライセンスで公開されています。
本記事ではこれをGoogle Colabで実行してみたいと思います。
前準備
Google Colabを開き、今回使用する上記のリポジトリをクローンするとともに、必要なライブラリもインストールします。Google Colabは基本的なライブラリがインストールされた状態になっているので、別途必要なのはrtreeだけでした。また、リポジトリの中のスクリプトをインポートできるようにパスを通しておきます。
!pip install rtree
!git clone https://github.com/motion-planning/rrt-algorithms.git
# パスを通す
import sys
sys.path.append("/content/rrt-algorithms/")プログラムを一部変更します。
クローンしたリポジトリの中にふくまれているrrt-algorithms/src/utilities/plotting.pyをダブルクリックをして開くと、
self.filename = "../../output/visualizations/" + filename + ".html"が見つかると思いますが、Colab環境では上手く動作しないため、self.filename = filename + ".html"に変更します。変更したら、Ctrl + Cで保存しましょう。
プログラムを開くのが面倒な場合は、以下のコマンドを使って書き換えても問題ありません。
!sed -i 's/"..\/..\/output\/visualizations\/"\ +//g' /content/rrt-algorithms/src/utilities/plotting.pyこれで利用する準備だ整いました。
サンプルプログラムを試す
上記のリポジトリには、サンプルプログラムが入っているので、それを参考に一部(障害物情報)変更したものをColabのセルで実行してみます。
以下のプログラムを実行して、必要なものをインポートしましょう。
import numpy as np
from src.rrt.rrt import RRT
from src.search_space.search_space import SearchSpace
from src.utilities.plotting import PlotRRT探索における各種パラメータと探索空間の設定をします。
# 空間設定を2次元平面上の一辺が140の正方形とする
X_dimensions = np.array([(0, 140), (0, 140)])
# 障害物情報は長方形の始点座標と終点座標の組み合わせ(例:始点(20, 60)、終点(40, 80)のときは(20, 60, 40, 80)にする)
Obstacles = np.array([(20, 20, 40, 40), (20, 60, 40, 80), (20, 100, 40, 120),
(60, 20, 80, 40), (60, 60, 80, 80), (60, 100, 80, 120),
(100, 20, 120, 40), (100, 60, 120, 80), (100, 100, 120, 120)])
# 開始点
x_init = (0, 0)
# ゴール点
x_goal = (140, 140)
# エッジの長さ(最初は長いエッジを使って探索しうまくたどり着けなかった場合は短いエッジで試すため長いものから格納する。(16, 8, 4, 2)など。)
Q = np.array([(8, 4)])
r = 1 # 障害物との交差を検証する最小長
max_samples = 1024 # 最大のサンプリング回数
prc = 0.1 # ゴールに到達したか確認する確率
# 空間設定と障害物情報から実際の探索空間を作成
X = SearchSpace(X_dimensions, Obstacles)RRT探索を実行します。
# 上記情報からRRT探索を実行しパスを取得
rrt = RRT(X, Q, x_init, x_goal, max_samples, r, prc)
path = rrt.rrt_search()可視化します。
plot = Plot("rrt_2d")
plot.plot_tree(X, rrt.trees)
if path is not None:
plot.plot_path(X, path)
plot.plot_obstacles(X, Obstacles)
plot.plot_start(X, x_init)
plot.plot_goal(X, x_goal)
plot.draw(auto_open=False)htmlファイルが生成されるので、表示してみます。
ランダムに枝を伸ばすことでゴールにたどり着けていることが分かります。
RRTはランダムに探索をするため、毎回ルートが異なります。もう一回実行してみましょう。私の場合、以下のような結果になりました。
RRTは最適化に基づいてパスプランニングを行う手法ではないため、このように毎回異なる結果になります。また、探索に要する時間も、探索の進みに依存しますし、必ずゴールにたどり着くとは限りません。運が悪いと、ゴールにたどり着く前に最大探索回数に達して探索失敗になる可能性があります。MoveItというROSの動作プランニングパッケージでRRTによるロボットの軌道生成を試したことがある方であれば分かるかもしれませんが、人間から見れば明らかに到達可能な範囲であっても、探索が上手く進まず軌道生成を失敗することが多々あります。その場合は、RRTの最大探索回数を増やしてあげることで対応できるはずです(確認はしていないです。あくまでも仮説です)。
MoveItを用いたmyCobotの制御は以下の記事で説明しました。
それでは、3次元空間におけるRRTによるパスプランニングも試してみたいと思います。3次元を扱うときは、空間設定を3次元のある範囲にし、障害物情報は直方体の3次元座標の始点と終点にします。
# 空間設定を3次元平面上の一辺が140の立方体とする
X_dimensions = np.array([(0, 140), (0, 140), (0, 140)]) # dimensions of Search Space
# 障害物情報。これは直方体の始点座標と終点座標の組み合わせ。
Obstacles = np.array(
[(20, 20, 20, 40, 40, 40), (20, 20, 60, 40, 40, 80), (20, 20, 100, 40, 40, 120),
(20, 60, 20, 40, 80, 40), (20, 60, 60, 40, 80, 80), (20, 60, 100, 40, 80, 120),
(20, 100, 20, 40, 120, 40), (20, 100, 60, 40, 120, 80), (20, 100, 100, 40, 120, 120),
(60, 20, 20, 80, 40, 40), (60, 20, 60, 80, 40, 80), (60, 20, 100, 80, 40, 120),
(60, 60, 20, 80, 80, 40), (60, 60, 60, 80, 80, 80), (60, 60, 100, 80, 80, 120),
(60, 100, 20, 80, 120, 40), (60, 100, 60, 80, 120, 80), (60, 100, 100, 80, 120, 120),
(100, 20, 20, 120, 40, 40), (100, 20, 60, 120, 40, 80), (100, 20, 100, 120, 40, 120),
(100, 60, 20, 120, 80, 40), (100, 60, 60, 120, 80, 80), (100, 60, 100, 120, 80, 120),
(100, 100, 20, 120, 120, 40), (100, 100, 60, 120, 120, 80), (100, 100, 100, 120, 120, 120)]
)
x_init = (0, 0, 0) # スタート位置
x_goal = (140, 140, 140) # ゴール位置これ以降は、2次元のときと同様です。探索を実行し、可視化したときの結果は以下の通りです。
これ以上、図を押せるとページが激重になるので、これくらいで終わりにしますね。
まとめ
私はRRTについて聞いたことがあるけど軌道生成や経路生成で使われる方法だし難しそうというイメージをもっていたのですが、実際、内部を知ってしまえば、単純で理解しやすいアルゴリズムでした。RRTには、改良版が複数あるみたいなので、それらについても調べてみたいですね。
最後までお読みいただきありがとうございました。