方策勾配法と方策勾配定理の導出

本記事では、強化学習において重要な最適化方法の1つである方策反復法の具体的な手法の方策勾配法について解説するとともに、そこで使用する方策勾配定理について導出も示していきます。

はじめに

強化学習で使用する最適化手法は、大きく分けて、方策反復法をベースとするものと価値反復法をベースとするものがあります。方策反復法と価値反復法は、動的計画法を用いたプランニング問題で使用するものです。強化学習問題では、最適な方策を求めることが目標になるため、両手法の主な違いは、その方策を直接モデル化するか、価値を用いてモデル化するかの違いになります。

本記事のテーマである方策勾配法は、方策反復法の1つで、方策をパラメータ\(\theta\)で直接モデル化し、目的関数\(J(\theta)\)の勾配を用いて最適な方策を求める手法です。

方策勾配法

方策勾配法とは、方策をパラメータ\(\theta\)で直接モデル化し、期待収益\(J(\theta)\)を目的関数として勾配を用いて最適化します。学習率を\(\alpha\)と置くと、方策勾配法は以下のように表されます。

$$
\theta \leftarrow \theta + \alpha\nabla_\theta J(\theta)
$$

ニューラルネットワークについて学んだことがある方なら、このようなパラメータ更新方法には馴染みがあると思いますが、誤差関数を最小化するときに使用する勾配降下法の逆、勾配上昇法です。なぜ勾配上昇法を使用するかというと、目的関数が誤差関数の場合の最適化問題は目的関数の最小化ですが、目的関数が期待収益の場合の最適化問題は目的関数の最大化だからです。

方策勾配法を利用するには、期待収益\(J(\theta)\)の勾配\(\nabla_\theta J(\theta)\)を求める必要があります。そのためには、期待収益を何で定義するかを考える必要があります。期待報酬は方策の良さを表して欲しいため、一般的には、状態価値関数を使用します。

$$
J(\theta) = V^\pi(s)
$$

このとき、以下の方策勾配定理により期待収益の勾配が定義されます。

$$
\nabla_\theta J(\theta) = \mathbb{E}_\pi\left[\nabla_\theta\ln\pi_\theta(a|s)Q^\pi(s,a)\right]
$$

以降では、この方策勾配定理について導出していきます。

基礎知識

方策勾配定理の証明は難易度が高く、また、状態価値関数の定義方法によって若干、導出が異なるため、本記事ではそれらについても触れながら解説していきますが、そこで必要となる基礎知識について、ここでは述べていきます。

ここで説明する基礎知識は、基本的に以下の記事から重要な部分を抜粋したもの＋αになります。

マルコフ決定過程

強化学習で使用する報酬、状態価値、行動価値関数は、マルコフ決定過程(Markov Decision Process: MDP)に基づいて定義されています。マルコフ決定過程は、次の状態は現在の状態と行動にのみに依存して決定されるという性質を持つ状態を考えます。

マルコフ決定過程は以下で定義されます。

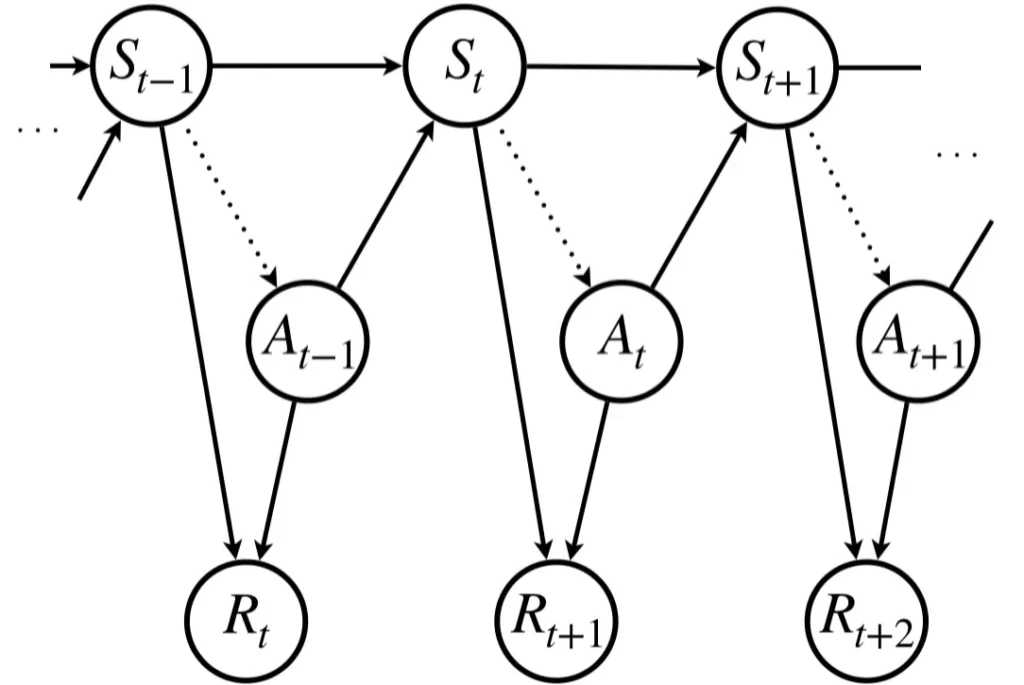
下図は、現在の時刻を\(t\)としたとき、現在の状態\(s_t\)で方策\(\pi\)に従って行動\(a_t\)を実施したら、報酬\(R_{t+1}\)が得られ、時状態\(s_{t+1}\)に遷移する状況を表しています。ちなみに、確率変数は大文字、既に決定したら小文字という使い分けしています。図では、全て確率変数として表していますが、文章では基本的に小文字を使用していくことになると思います。

累積報酬和と割引報酬和

報酬和とは、即時報酬\(R\)を加算したものをいいます。加算方法によって2種類の報酬和を考えることができます。1つ目は、累積報酬和で、現在から未来にかけて得られる報酬を全て同じスケールで加算していきます。ただし、この場合は発散してしまう可能性があるため、ある程度で打ち切る必要があります。2つ目は、割引報酬和で、現在から未来にかけて割引率によって即時報酬の値を割引ながら加算していきます。

累積報酬和

$$
G_t = R_{t+1} + R_{t+2} + \cdots + R_{t+K} = \sum_{k=0}^{K-1} R_{t + k + 1}
$$

割引報酬和

$$
G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^\infty \gamma^k R_{t + k + 1}
$$

状態価値関数

状態価値関数とは

状態価値関数とは、マルコフ決定過程における状態に注目して、その価値を定量化したもので、以下のように定義されます。

$$
V^{\pi}(s) = \mathbb{E}_{\pi}[G_t|S_t=s]
$$

状態価値関数とベルマン方程式

ここでは、割引報酬和を用いた場合の状態価値関数とベルマン方程式について紹介します。

$$
V^{\pi}(s) = \sum_{a\in A}\pi(a|s)\sum_{s'\in S}P(s'|s, a)\left[r(s, a) + \gamma V^{\pi}(s') \right]
$$

累積報酬和を使用する場合の状態価値関数のベルマン方程式は上式から\(\gamma\)を取り除いたものになります。

細かい導出は以下のページをご参照ください。

行動価値関数

行動価値関数とは

行動価値関数とは、マルコフ決定過程における状態と行動に注目して、その価値を定量化したもので、以下のように定義されます。

$$
Q^{\pi}(s, a) = \mathbb{E}_{\pi}[G_t|S_t=s, A_t=a]
$$

行動価値関数のベルマン方程式

ここでは、割引報酬和を用いた場合の行動価値関数とベルマン方程式について紹介します。

$$\begin{eqnarray}
Q^\pi (s, a) &=& r(s, a) + \gamma \sum_{s'\in S} P(s'|s, a)V^\pi (s')\\
&=& r(s, a) + \gamma \sum_{s'\in S} \sum_{a'\in A} P(s'|s, a)\pi (a'|s') Q^\pi (s', a')
\end{eqnarray}$$

累積報酬和を使用する場合の行動価値関数のベルマン方程式は上式から\(\gamma\)を取り除いたものになります。

細かい導出は以下のページをご参照ください。

状態価値関数と行動価値関数の関係

上で状態価値関数と行動価値関数について解説しましたが、方策勾配定理の導出では、これらの関係を用いた置き換えを頻繁に用いますので、改めて確認しておきたいと思います。

パラメータ\(\theta\)によってモデル化された方策を\(\pi_\theta(a|s)\)、状態価値関数を\(V^\pi(s)\)、行動価値関数を\(Q^\pi(s, a)\)と置いたとき、両者は以下のような関係を持ちます。

$$\begin{eqnarray}
V^\pi(s) &=& \sum_{a\in\mathcal{A}}\pi_{\theta}(a|s)Q^\pi(s,a) \\
Q^\pi(s,a) &=& r(s,a)+\gamma\sum_{s'\in\mathcal{S}}P(s'|s,a)V^\pi(s')
\end{eqnarray}$$

上式は有限離散状態・有限離散行動の環境に、利得として割引報酬和を用いて状態価値関数と行動価値関数を定義した場合になります。

1つ目の式は、状態\(s\)の状態価値は、方策\(\pi_\theta(a|s)\)に従って状態\(s\)における行動価値\(Q^\pi(s, a)\)の全行動について方策で期待値を計算したものとなることを表しています。

2つ目の式は、状態\(s\)で行動\(a\)を行ったときの行動価値は、その時の即時報酬\(r(s,a)\)と次の状態\(s'\)における状態価値\(V^\pi(s')\)をその時の状態遷移確率\(P(s'|s,a)\)で期待値を取ったものについて割引率\(\gamma\)を乗算したものを足したものであることを表しています。

方策勾配定理

方策勾配定理とは

方策勾配定理とは、方策勾配法において、その勾配が以下の式で表されることを表した定理です。

$$
\nabla_\theta J(\theta) = \mathbb{E}_\pi\left[\nabla_\theta\ln\pi_\theta(a|s)Q^\pi(s,a)\right]
$$

方策勾配定理の導出

方策勾配定理の導出では、状態価値関数を累積報酬和の期待値とした場合と割引報酬和の期待値とした場合で若干異なります。

置き換えルール

方策勾配定理の導出では、再起的に登場する数式があり、それらを文字で置くことで数式変形を見やすくすることができます。そこで、置き換えルールを以下のように定めることにします。

$$
f(s) = \sum_{a\in\mathcal{A}}\nabla_{\theta}\pi_{\theta}(a|s)Q^\pi(s,a)
$$

$$
p^\pi_1(s\rightarrow s') = \sum_{a\in\mathcal{A}}\pi_{\theta}(a|s)P(s'|s,a)
$$

$$
p^\pi_2(s\rightarrow s') = \sum_{x\in\mathcal{S}}p^\pi_1(s\rightarrow x) p^\pi_1(x\rightarrow s')
$$

$$
\nabla \pi_\theta = \pi_\theta \nabla \ln\pi_\theta
$$

$$
\eta(s') = \sum_{t=0}^\infty\gamma^tp_t^\pi(s\rightarrow s')
$$

$$
\mu(s') = \frac{\eta(s')}{\sum_{x\in\mathcal{S}}\eta(x)}
$$

割引報酬和を用いた場合

$$\begin{eqnarray}
\nabla_{\theta}V^\pi(s) &=& \nabla_{\theta}\sum_{a\in\mathcal{A}}\pi_{\theta}(a|s)Q^\pi(s,a) \\
&=& \sum_{a\in\mathcal{A}}\nabla_{\theta}\pi_{\theta}(a|s)Q^\pi(s,a) + \sum_{a\in\mathcal{A}}\pi_{\theta}(a|s)\nabla_{\theta}Q^\pi(s,a) \\
&=& f(s) + \sum_{a\in\mathcal{A}}\pi_{\theta}(a|s)\nabla_{\theta}\left(r(s,a)+\gamma\sum_{s'\in\mathcal{S}}P(s'|s,a)V^\pi(s')\right) \\
&=& f(s) + \gamma\sum_{a\in\mathcal{A}}\pi_{\theta}(a|s)\sum_{s'\in\mathcal{S}}P(s'|s,a)\nabla_{\theta}V^\pi(s') \\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}\sum_{a\in\mathcal{A}}\pi_{\theta}(a|s)P(s'|s,a)\nabla_{\theta}V^\pi(s') \\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')\nabla_{\theta}V^\pi(s') \\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')\nabla_{\theta}\sum_{a'\in\mathcal{A}}\pi_{\theta}(a'|s')Q^\pi(s', a') \\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')\left(\sum_{a'\in\mathcal{A}}\nabla_{\theta}\pi_{\theta}(a'|s')Q^\pi(s',a') + \sum_{a'\in\mathcal{A}}\pi_{\theta}(a'|s')\nabla_{\theta}Q^\pi(s',a')\right)\\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')\left(f(s') + \sum_{a'\in\mathcal{A}}\pi_{\theta}(a'|s')\nabla_{\theta}Q^\pi(s',a')\right)\\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')f(s') + \gamma^2\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')\sum_{a'\in\mathcal{A}}\pi_{\theta}(a'|s')\sum_{s''\in\mathcal{S}}P(s''|s',a')\nabla_{\theta}V^\pi(s'') \\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')f(s') + \gamma^2\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')\sum_{s''\in\mathcal{S}}p_1^\pi(s'\rightarrow s'')\nabla_{\theta}V^\pi(s'') \\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')f(s') + \gamma^2\sum_{s''\in\mathcal{S}}\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')p_1^\pi(s'\rightarrow s'')\nabla_{\theta}V^\pi(s'') \\
&=& f(s) + \gamma\sum_{s'\in\mathcal{S}}p_1^\pi(s\rightarrow s')f(s') + \gamma^2\sum_{s''\in\mathcal{S}}p_2^\pi(s\rightarrow s'')\nabla_{\theta}V^\pi(s'') \\
&=& \sum_{s'\in\mathcal{S}}\sum_{t=0}^\infty\gamma^tp_t^\pi(s\rightarrow s')f(s') \\
&=& \sum_{s'\in\mathcal{S}}\eta(s')f(s') \\
&=& \sum_{s'\in\mathcal{S}}\eta(s')\sum_{a\in\mathcal{A}}\nabla_{\theta}\pi_{\theta}(a|s')Q^\pi(s',a) \\
&=& \sum_{x\in\mathcal{S}}\eta(x)\sum_{s'\in\mathcal{S}}\frac{\eta(s')}{\sum_{x\in\mathcal{S}}\eta(x)}\sum_{a\in\mathcal{A}}\nabla_{\theta}\pi_{\theta}(a|s')Q^\pi(s',a) \\
&\propto& \sum_{s'\in\mathcal{S}}\frac{\eta(s')}{\sum_{x\in\mathcal{S}}\eta(x)}\sum_{a\in\mathcal{A}}\nabla_{\theta}\pi_{\theta}(a|s')Q^\pi(s',a) \\
&=& \sum_{s'\in\mathcal{S}}\mu(s')\sum_{a\in\mathcal{A}}\nabla_{\theta}\pi_{\theta}(a|s')Q^\pi(s',a) \\
&=& \sum_{s'\in\mathcal{S}}\mu(s')\sum_{a\in\mathcal{A}}\pi_{\theta}(a|s')\nabla_{\theta}\ln\pi_{\theta}(a|s')Q^\pi(s',a) \\
&=& \sum_{s'\in\mathcal{S}}\sum_{a\in\mathcal{A}}\pi_{\theta}(a|s')\mu(s') \left[\nabla_{\theta}\ln\pi_{\theta}(a|s')Q^\pi(s',a)\right]
\end{eqnarray}$$

以上より、

$$
\nabla_\theta J(\theta) = \mathbb{E}_\pi\left[\nabla_\theta\ln\pi_\theta(a|s)Q^\pi(s,a)\right]
$$

となります。

累積報酬和の場合は、今までと同様で\(\gamma\)を取り除けば良いです。割引報酬和の方で勾配法策定理が導出できれば、累積報酬和の場合については簡単でしょう。

まとめ

本記事では、方策勾配法について紹介するとともに、方策勾配定理の導出について紹介してきました。これより、方策勾配法は

$$
\theta \leftarrow \theta + \alpha\nabla_\theta J(\theta)
$$

$$
\nabla_\theta J(\theta) = \mathbb{E}_\pi\left[\nabla_\theta\ln\pi_\theta(a|s)Q^\pi(s,a)\right]
$$

のように表すことができることを示すことができました。