逐次意思決定問題
逐次意思決定問題とは、逐次意思決定のルールである方策を最適化する問題です。方策について信号の例を用いて補足すると、信号が赤なら停止、信号が青なら前進というルールが方策で、「信号が赤」・「信号が青」という状態から「停止」・「前進」という行動へのマッピングになります。この、状態から行動へのマッピングを最適化するのが、逐次位置決定問題になるのです。これを解くには、方策の良し悪しを判断するための目的関数が必要になります。目的関数をどのように求めるかに依存します。ここでは、強化学習問題の定式化に際して重要な位置づけであるマルコフ決定過程を用いて説明していきます。
マルコフ決定過程
マルコフ決定過程とは、状態と報酬、行動の3つにより体系化された有限状態・離散時間の確率過程です。具体的には、状態集合および行動集合を\(\mathcal{S}, \mathcal{A}\)として、時刻\(t\)のときの状態を\(s_t\in\mathcal{S}\)、ある方策(下図の点線矢印)に従って行動\(a_t\in\mathcal{A}\)を実行したとき、報酬\(R_{t+1}=r(s_t, a_t)\)が得られ、次状態\(s_{t+1}\in\mathcal{S}\)に遷移する確率的なプロセスを表現しています。
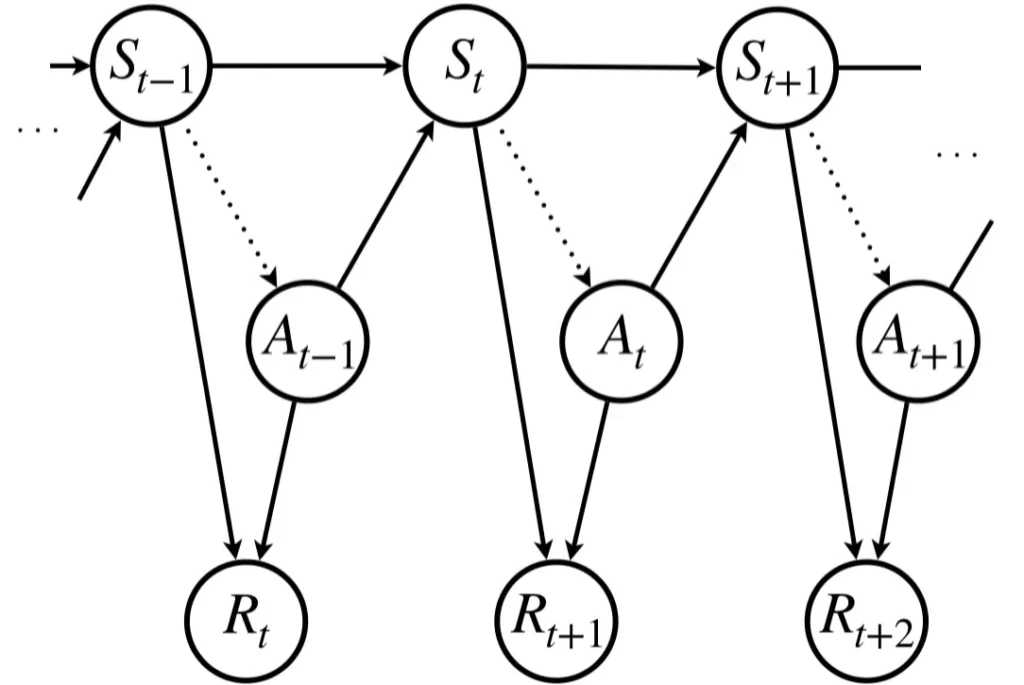
この流れをアニメーションにすると下図左のようになります。右は、マルコフ決定過程を環境とエージェントの2つの情報のやりとりとして表現したもので、環境では状態および報酬を計算し、エージェントでは行動を計算します。逐次意思決定問題は、方策の最適化問題であると説明した通り、何らかの方法を使用して方策を最適な状態にアップデートする必要がありますが、このアップデートのプロセスはエージェントの中身で完結します。
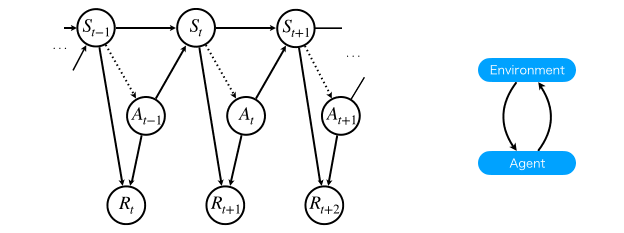
では、如何にしてエージェントを最適化するかということを考える必要があります。最適化の実現方法は、学習を伴うか否かで2つに分類することができます。環境側が既知、すなわち、エージェントが全ての状態遷移規則と報酬規則について知っている場合は、動的計画法などのソルバを用いることで実現することができます。これは、学習を伴いません。一方で、環境の状態遷移規則や報酬規則が未知の場合は、学習を用いて最適化する必要があります。前者は、地図を持った上で行動を選択するようなタスクなのでプランニング、後者は、地図がない状態で試行錯誤に基づき行動を選択するタスクなので強化学習と呼ばれています。
補足
機械学習において、学習とは、基本的に関数近似を意味します。強化学習では、何を関数近似するかで2つに分けることができ、試行錯誤ベースで状態から行動へのマッピングを関数近似する強化学習手法をモデルフリー強化学習、状態遷移規則と報酬規則を関数近似する手法をモデルベース強化学習と呼びます。
マルコフ決定過程についてさらに詳しく知りたい方は以下で解説しています。
逐次意思決定問題の種類
上で、既に触れてしましましたが、逐次位置決定問題は、環境モデルが既知の場合をプランニング、環境モデルが未知の場合を強化学習と呼ぶことを説明しました。
これを表にまとめると以下のようになります。
| 逐次意思決定問題 | |
| プランニング | 強化学習 |
| 環境モデルが既知 | 環境モデルが未知 |
動的計画法
動的計画法とはリチャード・アーネスト・ベルマン(Richard Ernest Bellman)が発展させた理論で、元の問題を部分問題に分け、部分問題の計算結果を記録しておき、何度も再利用することで計算の効率化を図る手法全般をいいます。
動的計画法には幾つか特徴があるので、それらについて説明していきます。
最適性の原理
全体で最適である意思決定は、どの部分をとってきても最適であるという原理を最適性の原理と呼びます。例えば、ある地点AからBまでの最短経路を考えます。この最短経路上にある点Cを置いたとき、距離ACはどこでも最短になっているということです。
多段決定問題
複数の目的を段階的に達成していく問題。
単に、ゴールを目指すだけの問題は多段決定問題とは言わない。
途中で鍵のかかったドアがあるから、ドアの鍵を探してからドアを開けないとゴールできないなどの問題を扱うのが多段決定問題である。
多段決定問題とプランニング
動的計画法は多段決定問題と呼ばれる最適化問題を解く手法で、モデルが既知の場合の方策を決定するプランニングは、多段決定問題とみなせるため、動的計画法を適用することができます。
方策反復法と価値反復法
ここでは、方策反復法と価値反復法について簡単に紹介します。これら2種類の反復法は、動的計画法を用いて最適な方策を計算するアルゴリズムです。これらは、深層強化学習でも用いられる重要な基本事項です。
方策反復法
方策反復法は再帰的な式構造をしており、動的計画法(メモ化再帰)を用いて計算することができます。
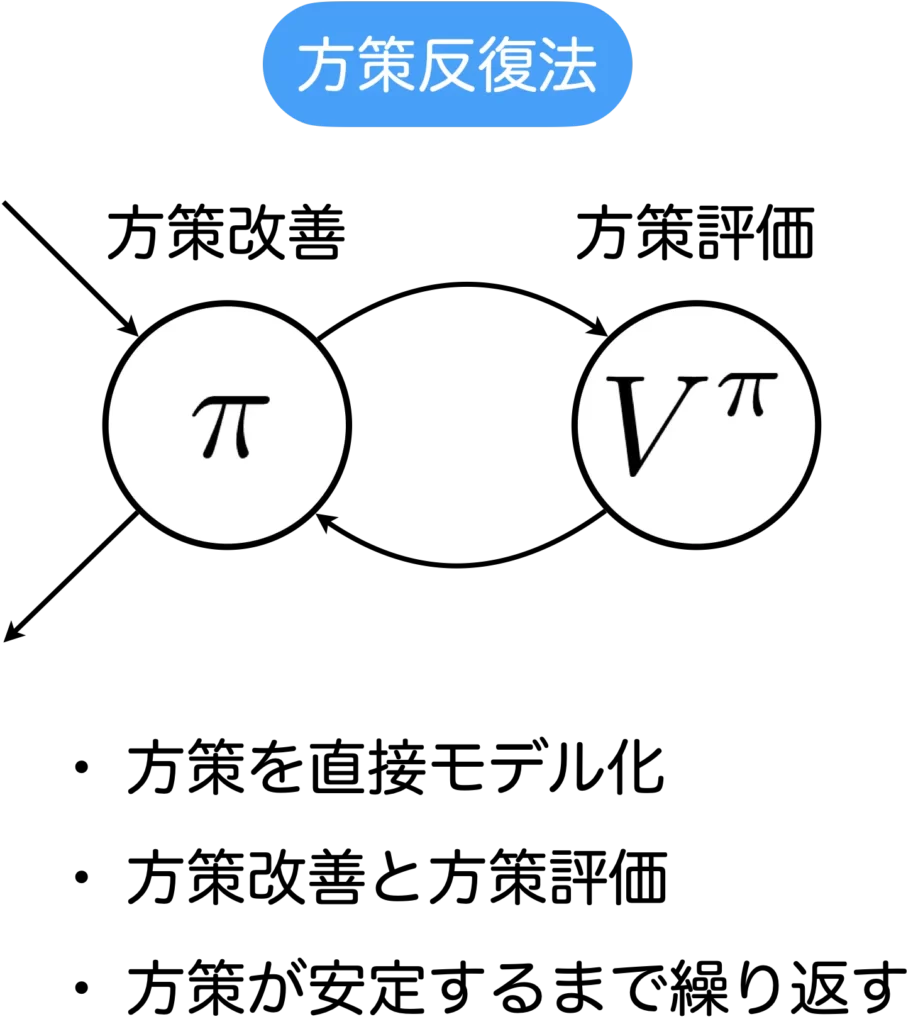
方策反復法は、方策改善ステップと方策評価ステップの2ステップからなります。方策改善ステップでは、各状態について行動価値関数が最大となる行動を出力する決定論的方策を計算し、方策改善ステップでは、現在の方策により求まる状態価値関数を動的計画法により求めます。このステップを繰り返し、方策が安定し変化しなくなったら終了します。
方策反復法のアルゴリズムを以下に示します。
以下では、状態集合を\(\mathcal{S}\)、行動集合を\(\mathcal{A}\)、状態数\(|\mathcal{S}|\)および\(|\mathcal{A}|\)は有限とします。
- 初期化
- 全ての状態\(s\in\mathcal{S}\)に対して、\(V(s)\)と\(\pi(s)\)を初期化する
- 方策評価
- 全ての状態に対して\(V(s) \leftarrow Q(s, \pi(s))\)で状態価値を更新
- 全ての状態価値の更新量が、ある閾値より小さくなるまで方策評価を反復
- 方策改善
- 全ての状態に対して\(pi(s) \leftarrow argmax_a Q(s, a)\)で方策を更新
- 方策の更新後の値が更新前と異なる状態が存在した場合は方策評価へ、存在しなければ終了
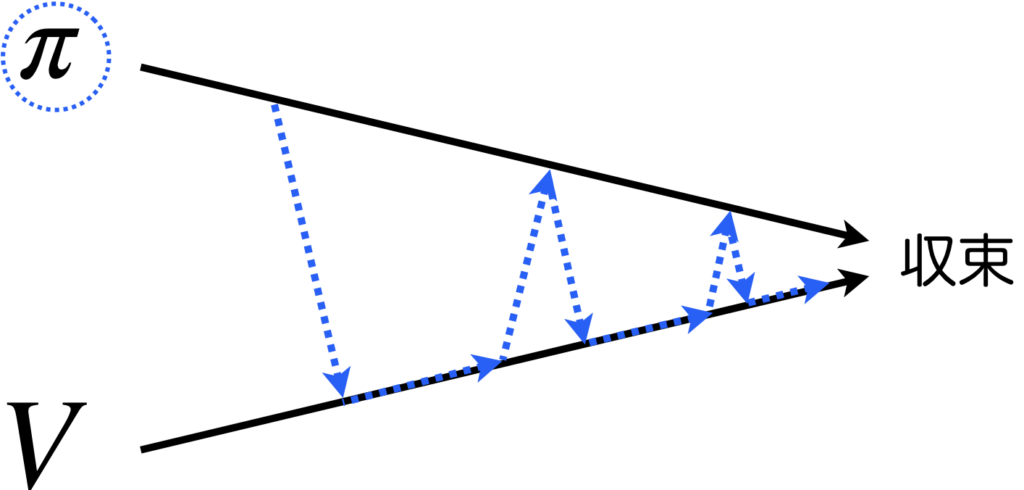
上のアルゴリズムに従ったときの、方策反復法における状態価値と方策の更新について流れを図にしました。まず最初の初期化ステップで、方策と状態価値は\(\pi_0, V_0\)として初期化されます。その後、方策評価ステップで方策\(\pi_0\)を全状態に対して評価します。一旦、全状態に対して評価を計算したとき、状態価値(〜評価値)が大きく更新された場合は、方策の評価が十分に行えていないということで、もう一度、全状態に対して評価を計算します。状態価値の変化量が閾値より小さくなるまで繰り返し、閾値より小さくなったら、方策改善ステップで方策\(\pi_0\)を更新し\(\pi_1\)とします。方策改善ステップ(赤の太矢印)ではargmaxを計算するため計算コストが高くなります。次は、\(\pi_1\)について評価します。方策が変化しなくなったら全体の処理を終了します。

最適な方策が得られるまでの流れのイメージは下図の様になります。青の点線で方策に丸をつけていますが、これは終了判定に方策を使うことを強調するためです。
価値反復法
価値反復法も再帰的な式構造をしており、動的計画法(メモ化再帰)を用いて計算することができます。
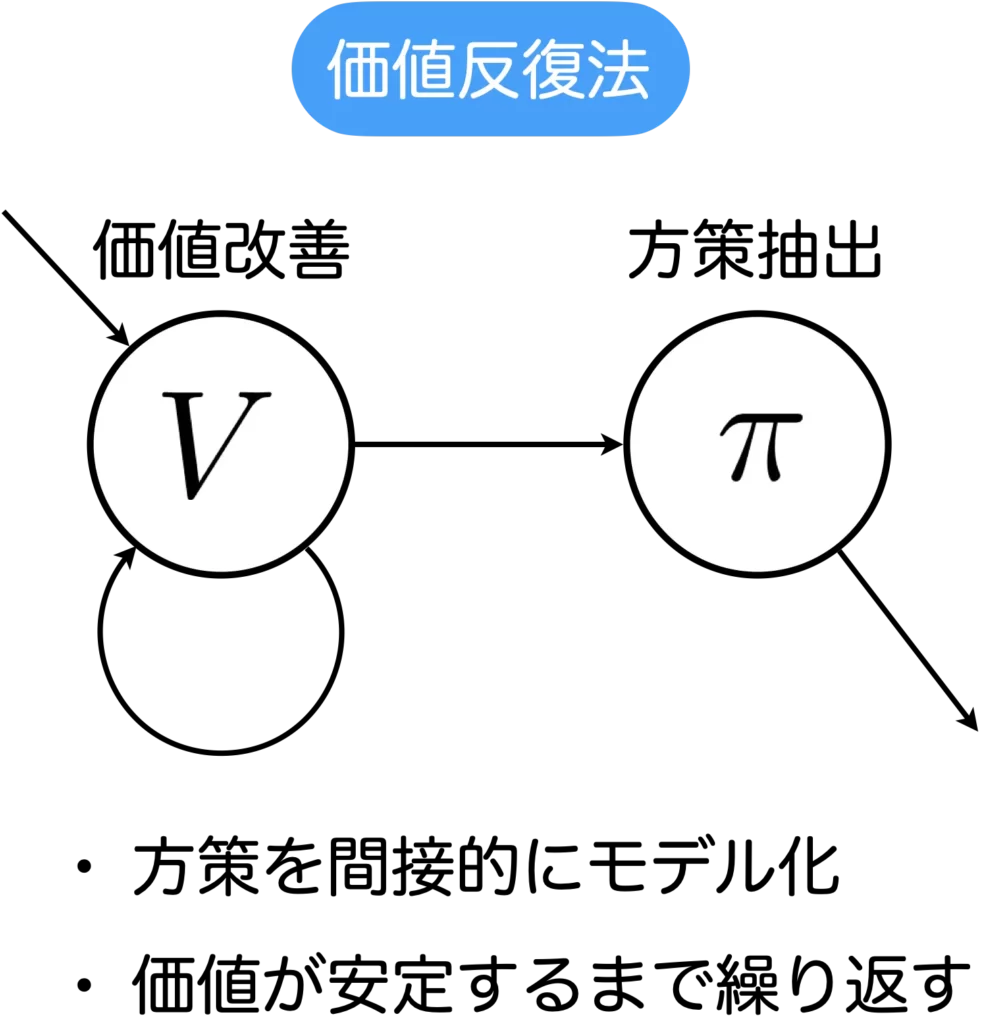
価値反復法は、価値改善ステップと方策抽出ステップがあり、価値改善を繰り返し行い、価値の更新量がある閾値より小さくなったら繰り返しを終了し、そこから方策を抽出します。
価値反復法のアルゴリズムを以下に示します。
- 初期化
- 全ての状態\(s\in\mathcal{S}\)に対して、\(V(s)\)を初期化する
- 価値改善
- 全ての状態に対して\(V(s) \leftarrow \max_a Q(s, a)\)で状態価値を更新
- 全ての状態価値の更新量が、ある閾値より小さくなるまで状態価値の更新処理を反復
- 方策抽出
- 全ての状態に対して\(pi(s) \leftarrow argmax_a Q(s, a)\)で方策を抽出して終了
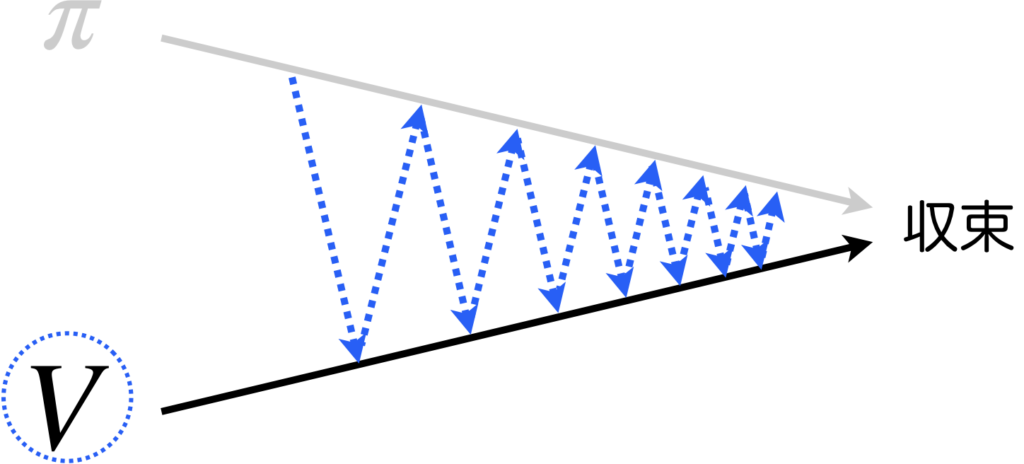
上のアルゴリズムに従ったときの更新のイメージを図を用いて説明します。価値反復法では方策抽出ステップより前には方策は登場しませんが、説明の便宜上で方策を導入して記載しています。細かい話ですが、最後のステップを方策抽出ステップと呼ぶように、実は価値改善ステップの中に方策に該当する処理が含まれています。該当する部分は行動価値のmaxを計算している部分です。この部分の処理は、argmaxで方策を更新し、その方策を使って行動を取得して行動価値を計算するのと等価です。内部に方策を持っているという考え方もできるので少しややこしいです。ですが、アルゴリズム的には抽出するまで方策は無い前提なので、色を薄くして記載しています。すると、以下のように記載できます。毎回、方策を更新して状態価値を計算しているというイメージになります。

方策反復法で示した図と同じような図を追加で示します。青の点線で状態価値に丸をつけていますが、これは終了判定に状態価値を使うことを強調するためです。
方策反復法と価値反復法の違い
アルゴリズムの細かい部分を理解しようとすると、方策反復法と価値反復法の違いが分からなくなって混乱することがあります。そのときは、以下を思い出してください。
方策反復法は、プロセスの終了判定は方策で、方策が安定するまで処理が行われます。方策の評価の際は、現在の方策を使ったときの状態価値を全状態に対して安定するまで計算します。安定したときの状態価値で方策を更新します。
価値反復法は、プロセスの終了判定は状態価値で、状態価値が収束すまで処理が行われます。
計算コストの点について補足すると、赤の太矢印が多い価値反復法は、計算が重くなりがちなので、方策反復法のほうが早く答えが出る傾向があります。
※余談ですが、方策反復法を発展させた深層強化学習アルゴリズムにActor-Critic、価値反復法を発展させたアルゴリズムにDQNなどがあります。
方策反復法の実装
まず最初に、今回使用する迷路環境とステップ毎にRBG画像データをモニターするラッパーをクローンし読み込みます。
# Gym環境を可視化するためのラッパーをclone
!git clone https://github.com/aakmsk/gymvideo.git
# 今回使用する迷路環境をclone
!git clone https://github.com/aakmsk/EasyMazeEnv.git
from gymvideo.scripts.gymvideo import GymVideo
from EasyMazeEnv.EasyMaze import EasyMazeここで使用する迷路環境は、以下の記事で紹介したものです。強化学習環境の自作に興味がある方は、ぜひ読んでみてください。
強化学習環境をインスタンス化し、同時にラッパーも適用します。
env = EasyMaze()
env = GymVideo(env)all_states = ["s0", "s1", "s2", "s3",
"s4", "s5", "s6", "s7",
"s8", "s9", "s10", "s11"]
all_actions = ["left", "top", "right", "down"]
# 状態価値関数と決定方策の初期値
V = {"s0":0, "s1":0, "s2":0, "s3":0,
"s4":0, "s5":0, "s6":0, "s7":0,
"s8":0, "s9":0, "s10":0, "s11":0}
PI = {"s0":"left", "s1":"left", "s2":"left", "s3":"left",
"s4":"left", "s5":"left", "s6":"left", "s7":"left",
"s8":"left", "s9":"left", "s10":"left", "s11":"left"}
# ダイナミクスを定義
def P_dynamics(next_state, state, action):
"""
state, next_state:s0~s11
action:left, top, right, down
"""
action_number = {"left":0, "top":1, "right":2, "down":3}
real_next_state = env.dynamics[state][action_number[action]]
if next_state == real_next_state:
return 1
else:
return 0
# 報酬関数を定義
def reward_fn(state, action):
if P_dynamics(next_state="s11", state=state, action=action):
return 1
else:
return 0
# 状態価値関数から行動価値関数を計算
def Q(state, action):
gamma = 0.9
q = 0
for next_state in all_states:
p_ = P_dynamics(next_state=next_state, state=state, action=action)
r_ = reward_fn(state=state, action=action)
v_ = V[next_state]
q = q + p_ * (r_ + gamma * v_)
return q方策評価と方策改善の関数を定義します。
threshold = 0.5
V_hist = []
def policy_evaluation():
delta = 0
for state in all_states:
temp = V[state]
action = PI[state]
V[state] = Q(state=state, action=action)
delta = max([delta, abs(V[state] - temp)])
V_hist.append(V.copy())
if delta > threshold:
policy_evaluation()
else:
policy_improvement()
def policy_improvement():
policy_stable = True
for state in all_states:
temp = PI[state]
value = [Q(state=state, action=all_actions[0]),
Q(state=state, action=all_actions[1]),
Q(state=state, action=all_actions[2]),
Q(state=state, action=all_actions[3])]
max_value = max(value)
PI[state] = all_actions[value.index(max_value)]
if temp != PI[state]:
policy_stable = False
if policy_stable == False: # 方策が安定でない
policy_evaluation()学習を行います。
policy_evaluation()学習を行った後に、動作を実行した時のアニメーションは以下のようになります。
価値の変遷は以下のようになります。
価値反復法の実装
all_states = ["s0", "s1", "s2", "s3",
"s4", "s5", "s6", "s7",
"s8", "s9", "s10", "s11"]
all_actions = ["left", "top", "right", "down"]
# 状態価値関数と決定方策の初期値
V = {"s0":0, "s1":0, "s2":0, "s3":0,
"s4":0, "s5":0, "s6":0, "s7":0,
"s8":0, "s9":0, "s10":0, "s11":0}
PI = {"s0":"left", "s1":"left", "s2":"left", "s3":"left",
"s4":"left", "s5":"left", "s6":"left", "s7":"left",
"s8":"left", "s9":"left", "s10":"left", "s11":"left"}
threshold = 0.5
V_hist = []
def optimal_value():
delta = 0
for state in all_states:
temp = V[state]
value = [Q(state=state, action=all_actions[0]),
Q(state=state, action=all_actions[1]),
Q(state=state, action=all_actions[2]),
Q(state=state, action=all_actions[3])]
V[state] = max_value = max(value)
delta = max([delta, abs(V[state] - temp)])
V_hist.append(V.copy())
if delta > threshold:
policy_evaluation()最適な価値を学習します。
optimal_value()学習後に最適な方策を抽出する関数です。
def get_policy():
for state in all_states:
value = [Q(state=state, action=all_actions[0]),
Q(state=state, action=all_actions[1]),
Q(state=state, action=all_actions[2]),
Q(state=state, action=all_actions[3])]
max_value = max(value)
PI[state] = all_actions[value.index(max_value)]get_policy()価値反復法の学習後のエージェントの動きや、価値の変化に関して、方策反復法と大差ないので省略します。
参考文献
Richard S. Sutton and Andrew G. Barto. “Reinforcement Learning: An Introduction.” MIT Press, 2018.