この記事では、強化学習の根幹部分を理解することを目標に、マルコフ過程・マルコフ報酬過程・マルコフ決定過程・部分観測マルコフ決定過程、そして関連する理論について分かりやすく解説していきたいと思います。
確率過程
マルコフ過程の解説を始める前に、確率過程とは何かを明らかにしたいと思います。
まず最初に株価の例を紹介します。株価は時間の変化と共に変動しますよね。その変動要因はさまざまで予測可能なものと予測不可能なものがあります。そのため、株価の変動をそのままモデル化(=数理的表現を用いて模型を作ること)するのは難しいでしょう。なぜなら、予測不可能なランダム要素を扱うことができないためです。では、どのようにしたら株価の変動を扱うことができるでしょうか。
その答えは株価の値を確率変数として扱うことです。確率変数を用いることで不確実性に対してロバストになるうえ、確率変数はある確率分布から生成されていると仮定しますから、その確率分布の変化をモデル化できれば、株価変動も数理的に表せます。
この話を簡潔にまとめると以下のようになるでしょう。
確率過程
確率過程の種類
確率過程にはどのような種類があるのかいくつか紹介したいと思います。以下で紹介する確率過程以外にもさまざまあるので、興味があれば調べることをお勧めします。
ウィーナー過程
連続時間確率過程の一種でブラウン運動の数理モデルです。次で紹介するガウス過程の一種でもあります。
ガウス過程
教師あり回帰問題に応用されています。
マルコフ過程
次の時刻の状態は前の時刻の状態のみに依存するというマルコフ性を満たした確率過程です。以降で詳しく説明します。
マルコフ過程の大前提 - マルコフ性 -
マルコフ性とは現在の状態を表す確率変数\(S_t\)が与えられたとき、次の状態\(S_{t+1}\)は\(S_t\)にのみ依存し、それ以前のどの状態\(S_0, S_1, \cdots, S_{t-1}\)に依存しないとう性質のことです。フランクに言うと状態遷移規則を単純化したルールです。
マルコフ性は数式により以下のように表現できます。
$$
P(S_{t+1}|S_t) = P(S_{t+1}|S_0, S_1,\cdots, S_t)
$$
マルコフ過程
定義
マルコフ過程(Markov Process: MP)は、マルコフ性を満たす確率過程のなかで最もナイーブなものです。
まずは、以下の例を見てイメージを掴みましょう。以下は状態遷移図と呼ばれるもので、ノードと辺で構成されています。以下の状態遷移図はある人の仕事内容の移り変わりだとしましょう。見方は、仕事Aのあとに、確率0.7で再度仕事A、確率0.2で仕事B、確率0.1で仕事Cが、仕事Bのあとに、確率0.7で再度仕事B、確率0.2で仕事C、確率0.1で仕事Aが、仕事Cのあとに、確率0.7で再度仕事C、確率0.2で仕事A、確率0.1で仕事Bが やってくるという感じです。実施中の仕事内容を状態とみなし、その後にやってくる仕事は、辺に示した確率により確率的にやってくるとしています。次にどの仕事がやってくるかは今実施中の仕事内容のみに依存します。
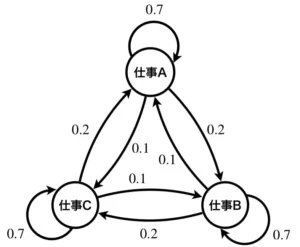
今示した例では具体的な状態を与えましたが、これを変数を使用し一般化した状態遷移図で表現すると、以下のように時間軸で展開されたグラフになります。これは、状態集合\(S=\{s_0, s_1, \cdots\}\)、それらの状態遷移確率を表す行列\(P\)が定義されれば決定できることから、\(\langle S, P\rangle\)として表記します。

マルコフ過程
where:
\(S\):状態の有限集合
\(P\):\(S×S\)で定義された状態遷移確率,\(P(S_{t+1}|S_t)\)
具体例
以下の問題を通じて理解を深めていきたいと思います。
問題
・A市在住の人は確率0.2でB市へ
・A市在住の人は確率0.1でC市へ
・B市在住の人は確率0.1でA市へ
・B市在住の人は確率0.2でC市へ
・C市在住の人は確率0.2でA市へ
・C市在住の人は確率0.1でB市へ
(1) このときの状態遷移図と遷移確率行列を求めよ。
(2) 今年のA, B, C市の実行をそれぞれ3000人、5000人, 2000人としたとき、今年の人口分布と来年の人口分布、再来年の人口分布をグラフで表せ。
(1) 状態遷移図は以下のようになります。
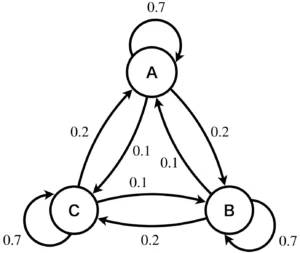
3市に在住の10000万人はA、B、Cのいずれかの状態を持ち、それぞれの状態が生起する確率は、各市に在住している人口を全人口10000人で除算したものとなり、年が進むごとに辺の確率で人口の流動が発生することが分かります。
\(t\)年におけるA, B, C市のそれぞれの人口を\(a_t, b_t, c_t\)としたとき、\(t+1\)年の人口\(a_{t+1}, b_{t+1}, c_{t+1}\)は以下の行列による変換で表すことができます。
$$
\left(\begin{matrix}
a_{t+1}\\
b_{t+1}\\
c_{t+1}
\end{matrix}\right)
=
\left(\begin{matrix}
0.7 & 0.1 & 0.2\\
0.2 & 0.7 & 0.1\\
0.1 & 0.2 & 0.7
\end{matrix}\right)
\left(\begin{matrix}
a_t\\
b_t\\
c_t
\end{matrix}\right)
$$
この行列
$$
\left(\begin{matrix}
0.7 & 0.1 & 0.2\\
0.2 & 0.7 & 0.1\\
0.1 & 0.2 & 0.7
\end{matrix}\right)
$$
が状態遷移行列です。
(2) 今年の各市の人口が順に3000人、5000人、2000人なので、確率分布は全人口で割った0.3、0.5、0.2になります。
来年の人口分布は、今年の人口分布に状態遷移行列を1回適用することで求まり、0.3、0.43、0.27になります。
再来年の人口分布は、来年の人口分布に状態遷移行列を1回適用することで求まり、0.307、0.388、0.305となります。
グラフにすると以下のようになります。
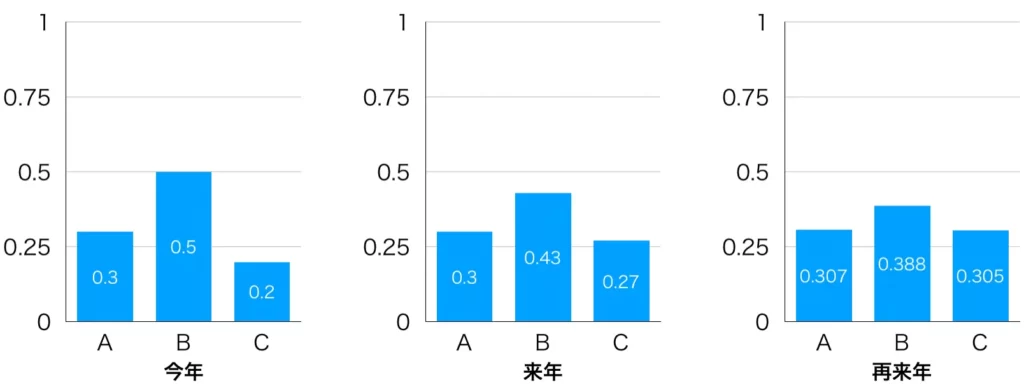
このように、人口の分布が変化することが分かります。10000万人から1人呼び出して、住んでいる市を尋ねたときに答えた市を表す確率変数を\(X\in\{A, B, C\}\)とし、その分布の変化を考えたとき、その変化は前年の人口分布に依存しているためマルコフ過程になります。
マルコフ報酬過程
マルコフ報酬過程(Markov Reward Process: MRP)とはマルコフ過程\(\langle S, P\rangle\)に報酬の概念\(R, \gamma\)を追加した\(\langle S, P, R, \gamma \rangle\)で表現される確率過程です。
先ほどマルコフ過程の時に示した状態遷移図に少し変更を加えたものを使用してイメージを掴みましょう。マルコフ過程のときと異なり、状態に数字が付いています。これが報酬です。以下の例の場合、仕事Aを引き受けたら報酬5、仕事Bを引き受けたら報酬10、仕事Cを引き受けたら報酬-2という感じです。
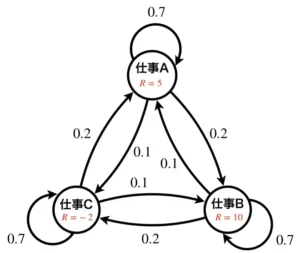
マルコフ報酬過程を一般化した状態遷移図で表すと以下のようになります。
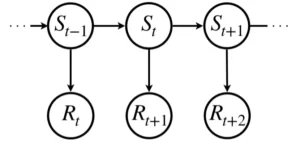
マルコフ報酬過程では報酬の概念を定義したことで、次に示す割引報酬和を導入することができます。割引報酬和とは各ステップで得られる即時報酬に対して、遠い未来の即時報酬であればあるほど小さく見積もるように割引率\(\gamma\in[0, 1]\)を乗算し足し上げたものです。時刻\(t\)の即時報酬を\(R_t\)とします。このときの割引報酬和\(G_t\)は以下の式で定義されます。
$$
G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^\infty \gamma^k R_{t + k + 1}
$$
マルコフ報酬過程
where:
\(S\):状態の有限集合
\(P\):\(S×S\)で定義された状態遷移確率
\(R\):全ての状態\(S\)にたいして定義された報酬関数,\(R_s = \mathbb{E} [R_{t+1}|S_t = s]\)
\(\gamma\):割引率,\(\gamma\in [0, 1]\)
マルコフ決定過程
マルコフ決定過程(Markov Decision Process: MDP)とはマルコフ報酬過程に行動を追加した確率過程で、\(\langle S, A, P, R, \gamma \rangle\)で表されます。
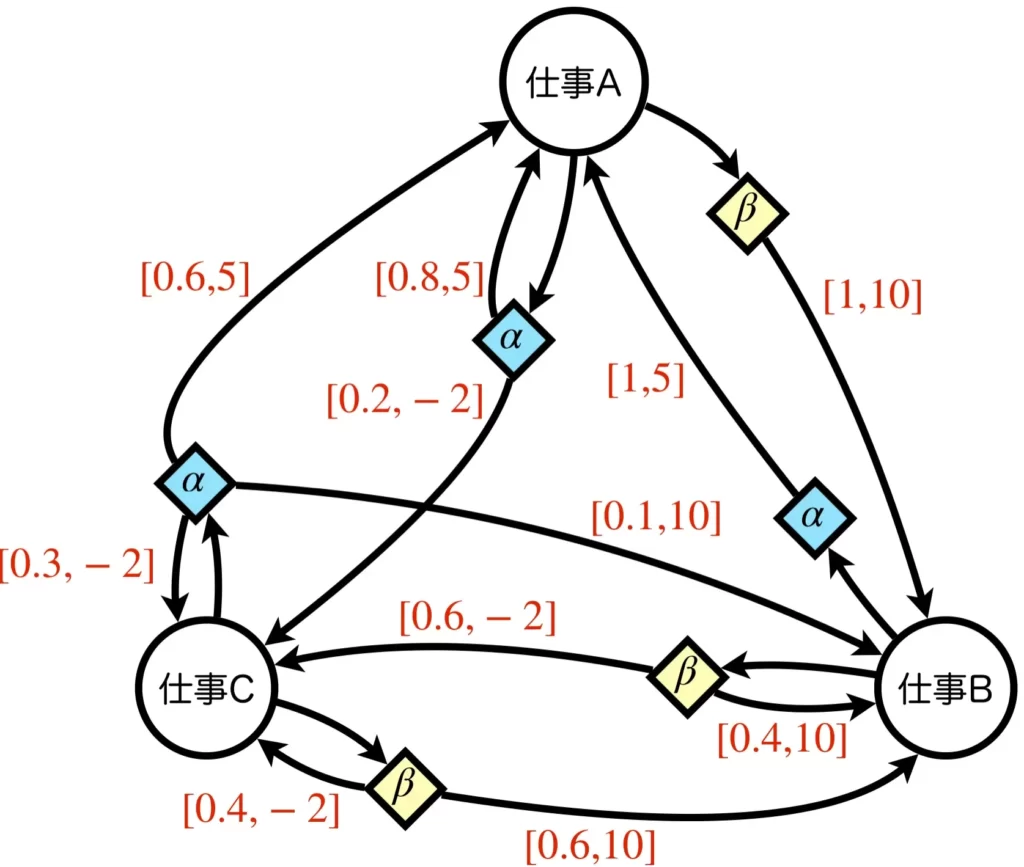
先ほどと同様に、例を見てみましょう。マルコフ過程やマルコフ報酬過程のときと異なり、行動の概念が追加されたことで、辺の数が増え複雑になっています。仕事Aという状態にいるときに行動\(\alpha\)をとったら確率0.8で仕事Aに遷移し報酬5、確率0.2で仕事Cに遷移し報酬-2、行動\(\beta\)をとったら確率1で仕事Bに遷移し報酬10がもらえるといった感じです。重要なのは、次の状態へ遷移する要因として、状態だけでなく行動も関わっている点です。
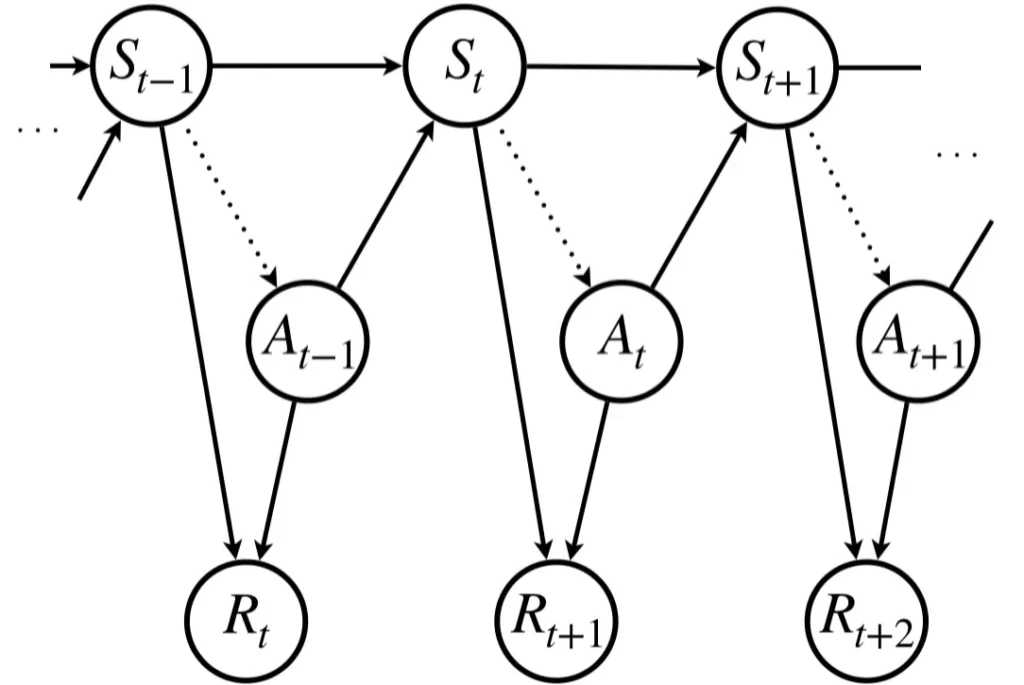
一般的にマルコフ決定過程として示される状態遷移図は次のようになります。状態\(S_t\)にいるとき、方策\(\pi\)(図中点線)に従って行動\(A_t\)を行い、\(S_{t+1}\)に遷移し、即時報酬\(R_{t+1}\)が得られるというプロセスをとります。
マルコフ決定過程
where:
\(S\):状態の有限集合
\(A\):行動の有限集合
\(P\):\(S×A×S\)で定義された条件付き状態遷移確率,\(P(S_{t+1}| S_t, A_t)\)
\(R\):\(S×A\)で定義された報酬関数,\(R(S_t, A_t)\)
\(\gamma\):割引率,\(\gamma\in [0, 1]\)
部分観測マルコフ決定過程
マルコフ決定過程では、全ての状態が観測できることを前提としていました。すなわち、観測を状態として扱える(=観測にマルコフ性がある)ことを仮定していたわけです。しかし、現実には観測にマルコフ性がない場合が多く、この場合に観測を状態として扱ってマルコフ決定過程に適用すると、マルコフ性がない観測をマルコフ性をあると仮定したマルコフ決定過程に強制的に落とし込もうとすることになるため、状態に混同が生じてしまい正しくモデル化できません。そのため、観測にマルコフ性を持たない対象は状態が観測できないとみなし新たな確率過程を導入する必要があります。
例えば、机の上に置いてあるリモコンを手に取る瞬間の画像と、リモコンを机の上に置く瞬間の画像を観測として得うる場合を考えてみます。この2つの動作は全く異なるはずですが、観測として得られた画像を比較しただけでは区別ができません。マルコフ決定過程において観測と状態は等価であり、観測にはマルコフ性があるものと考えますので、この観測を状態として扱うマルコフ決定過程では、異なるべき状態が同一の状態となってしまうます。
そこで、観測と状態を異なるものとして考えることにします。状態は必ずマルコフ性を持つ一方で、観測はマルコフ性を持つとは限らないとするわけです。広い見方をすれば、観測は状態を包含しますが、状態は観測を包含しません。
このような確率過程を部分観測マルコフ決定過程(Partially Observable Markov decision Process:POMDP)といいます。観測のある部分ではマルコフ性があるが、他の部分ではマルコフ性がないような、マルコフ決定過程が部分的にしか観測できないものをモデル化するときに使用します。部分観測マルコフ決定過程では、観測にマルコフ性がなくても、背後にマルコフ性を持つ状態が存在すると仮定します。マルコフ決定過程の一般化という解釈ができます。
一般的に示される部分観測マルコフ決定過程の状態遷移図を以下に示します。
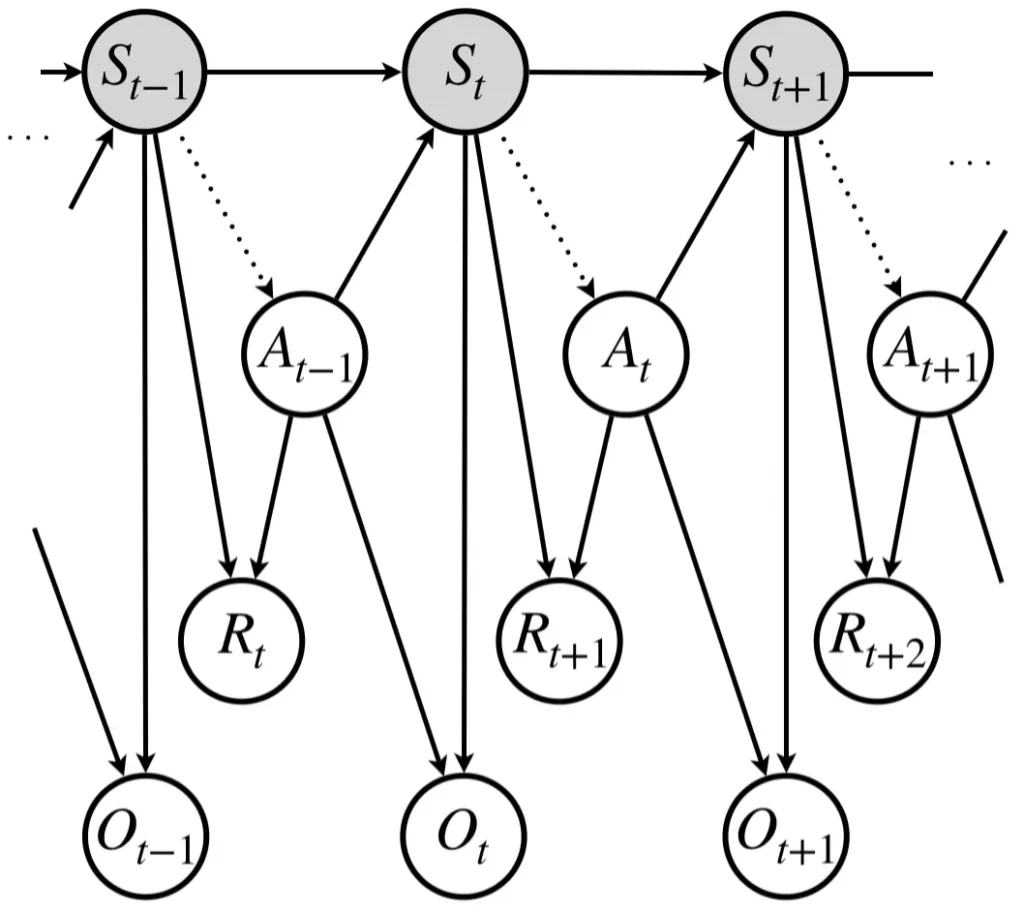
部分観測マルコフ決定過程
where:
\(S\):状態の有限集合
\(A\):行動の有限集合
\(P\):\(S×A×S\)で定義された条件付き状態遷移確率,\(P(S_{t+1}| S_t, A_t)\)
\(R\):\(S×A\)で定義された報酬関数,\(R(S_t, A_t)\)
\(\gamma\):割引率,\(\gamma\in [0, 1]\)
\(\Omega\):エージェントの観測の有限集合,\(o\in\Omega\)
\(O\):\(S×A×S\)で定義されたエージェントの観測を表す条件付確率,\(O(O_{t+1}|S_{t+1}, A_t)\)
それぞれの関係
マルコフ性というルールからスタートし、マルコフ過程、マルコフ報酬過程、マルコフ決定過程、部分観測マルコフ決定過程へと、機能を追加する形で紹介してきました。マルコフ過程からマルコフ報酬過程へは報酬の概念を追加することで、状態の相応しさを計測できるようにしました。マルコフ報酬過程からマルコフ決定過程へは、行動の不確実性を導入することで、意思決定の概念を追加しました。マルコフ決定過程から部分観測マルコフ決定過程へは、観測の不確実性を導入することで、実世界環境へ適用しやすいように一般化しました。
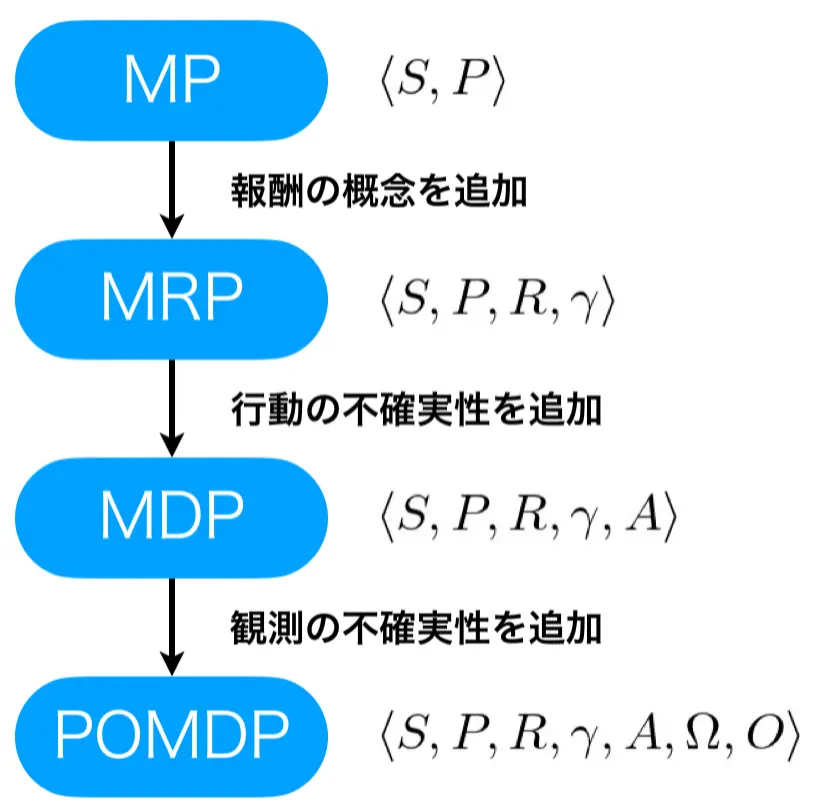
強化学習とマルコフ決定過程・部分観測マルコフ決定過程
強化学習とは
強化学習とは、エージェントと呼ばれる行動主体、より正確に言うと環境内のロボットを制御する信号を生成するアルゴリズムが、自分の報酬を最大化することを目的として行動獲得を目指す機械学習分野です。教師あり学習では直接答えが教えられ、それを正しく扱えるように学習しますが、強化学習では、直接答えが与えられることはなく、報酬という概念を使い間接的に良い行動であることを伝え、それを頼りに学習を行います。
強化学習を行うためには、強化学習環境と学習主体が必要です。分かりやすい例で考えると、強化学習環境は私たちが生活している実世界及び私たちの体、学習主体は脳です。脳は体に制御信号を送ることで体を動作させると同時に、転んで怪我したときには痛みがフィードバックされ、何が悪かったのか試行錯誤により学習します。
強化学習問題は、エージェントから環境へ送られる行動信号と、環境からエージェントに送られる観測と報酬をもつ確率的有限状態機械(確率的有限オートマトン)としてモデル化されています。
環境側
状態遷移関数:\(P(S_{t+1}|S_t, A_t)\)
観測関数:\(P(O_{t+1}|S_{t+1}, A_t)\)
報酬関数:\(\mathbb{E} [R_{t+1}|S_t, A_t]\)
エージェント側
状態遷移関数:<追記予定>
方策関数:<追記予定>
強化学習問題を行うには強化学習環境を生成し、その環境から観測として得られるものがマルコフ決定過程なのか部分観測マルコフ決定過程なのかを意識する必要があります。これを理解していないと、学習できないモデルで強化学習を実施しているなんてことにもなりえません。
そこで、強化学習環境がマルコフ決定過程の場合と部分観測マルコフ決定過程の場合のイメージを浮かべていただくために、それぞれについて解説します。
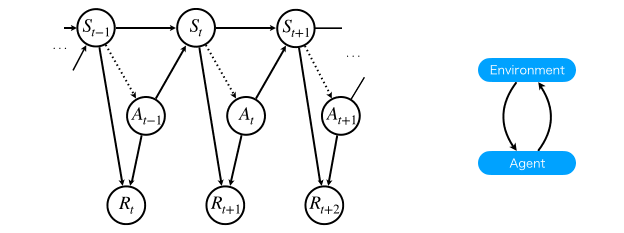
強化学習環境がマルコフ決定過程のとき
強化学習モデルが学習する方策は点線の矢印です。すなわち、マルコフ性をもつ状態から行動へのマッピングを学習します。
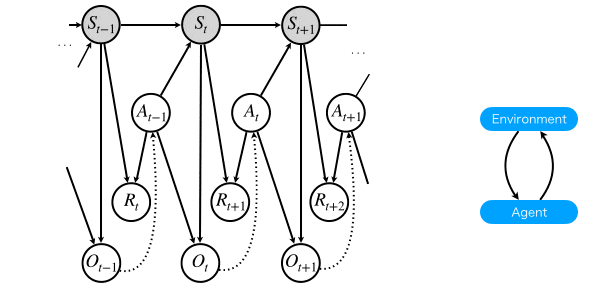
強化学習環境が部分観測マルコフ決定過程のとき
強化学習モデルが学習する方策は点線の矢印です。すなわち、マルコフ性を持つとは限らない観測から行動へのマッピングを学習します。
バックアップ線図
以降では、上で紹介したマルコフ決定過程に注目して、価値を定式化・式変形していきますが、その際にはバックアップ線図について理解しておくと大変理解がしやすいため先に紹介します。
バックアップ線図の描き方
状態は〇、行動は●で書きます。
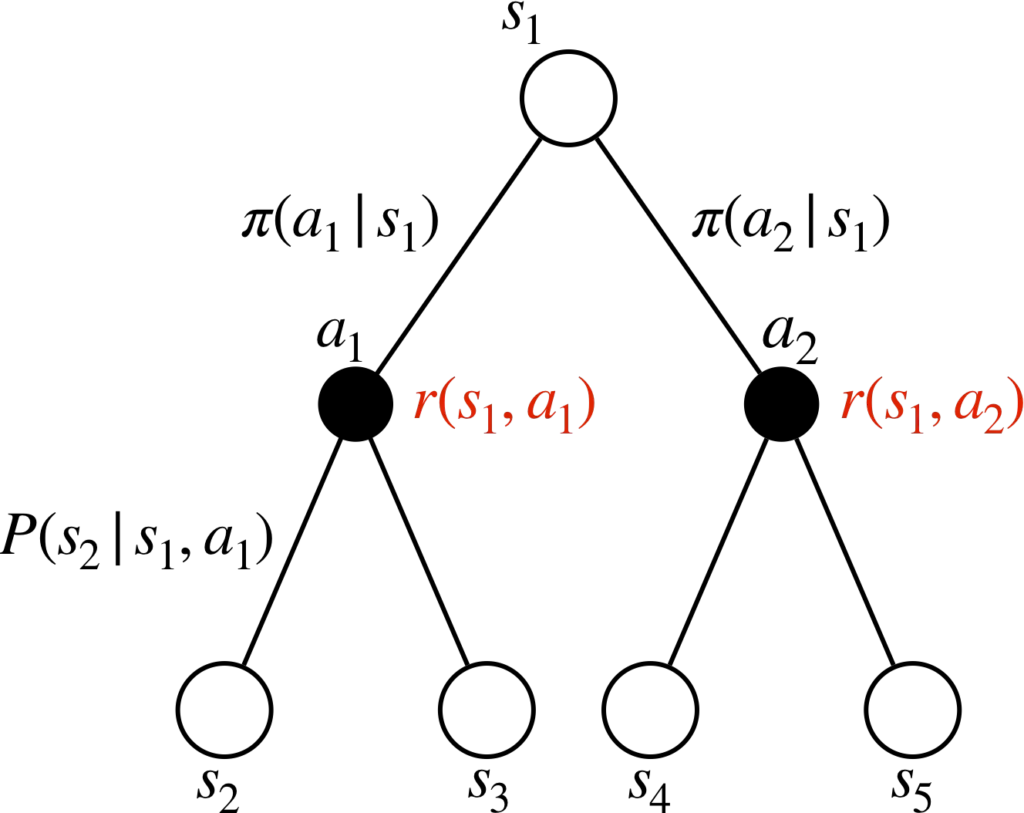
状態\(s_1\)のとき、行動\(a_1\)と\(a_2\)をとりえる場合、その確率は\(\pi (a_1|s_1)\)、\(\pi (a_2|s_1)\)で与えられます。ここで、行動が決定したら、報酬が決まります。
※この図においては、下付き文字は時刻ではなく種類を表しています。
マルコフ決定過程とベルマン方程式
マルコフ決定過程からベルマン方程式を導出していきます。
マルコフ決定過程では、ある状態\(s\)で行動\(a\)を実行して状態\(s'\)に遷移し、そのときの即時報酬が与えられる状況を考えました。
また、即時報酬に割引率\(\gamma\)を乗算しつつ、将来に渡り加算したものが割引報酬和\(G\)でした。
割引報酬和は、確率的な行動選択と状態遷移により変動する値であり、そのままだと使いにくいため期待値をとることにし、それを状態\(s\)の価値とすることにします。すなわち、
$$
V^{\pi}(s) = \mathbb{E}_{\pi}[G_t|S_t=s]
$$
とするわけです。時刻\(t\)の状態\(S_t\)が\(s\)のときの割引報酬和\(G_t\)の期待値を計算する形をとっています。これが状態価値関数です。
式の通りに考えると、状態価値関数の値を計算するには将来の全ての報酬が必要になりますが、マルコフ決定過程を仮定することでベルマン方程式が導出でき、現状態と次状態のみによる関係式で表すことができるようになります。
- 報酬関数\(R_{t+1} = r(S_t, A_t)\)
- 方策関数\(\pi(A_t|S_t) = P(A_t | S_t)\)
ベルマン方程式は、状態価値関数及び行動価値関数の場合についてそれぞれ定義でき、
$$
V^{\pi}(s) = \sum_{a\in A}\pi(a|s)\sum_{s'\in S}P(s'|s, a)\left[r(s, a) + \gamma V^{\pi}(s') \right]
$$
$$\begin{eqnarray}
Q^\pi (s, a) &=& r(s, a) + \gamma \sum_{s'\in S} P(s'|s, a)V^\pi (s')\\
&=& r(s, a) + \gamma \sum_{s'\in S} \sum_{a'\in A} P(s'|s, a)\pi (a'|s') Q^\pi (s', a')
\end{eqnarray}$$
補足ですが、上式から状態価値関数と行動価値関数の以下の関係が導けます。
$$
V^\pi (s) = \sum_{a\in A} \pi (a|s) Q^\pi (s, a)
$$
となります。これを実際に導出することで理解を深めたいところですが、式変形が複雑なので、以下のバックアップ線図を参考にしながら式を追っていきたいと思います。
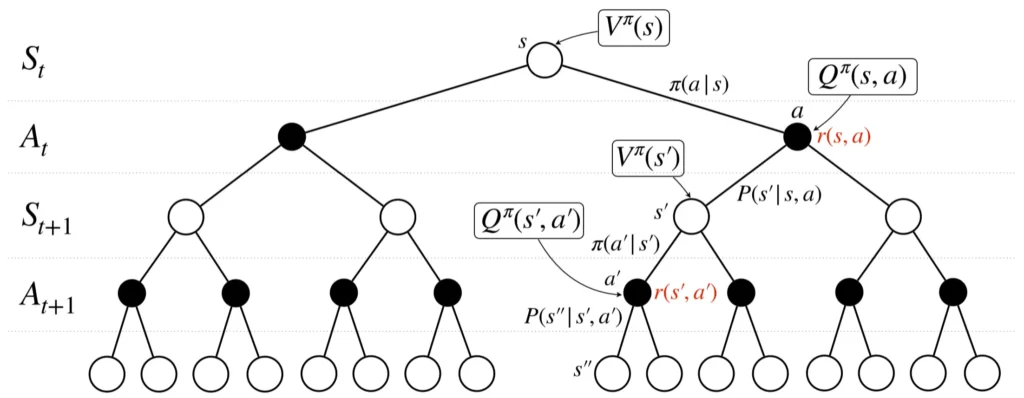
$$\begin{eqnarray}
V^{\pi}(s) &=& \mathbb{E}_{\pi}[G_t|S_t=s]\\
&=& \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1}|S_t=s]\\
&=& \mathbb{E}_{\pi}[R_{t+1}|S_t=s] + \gamma\mathbb{E}_{\pi}[G_{t+1}|S_t=s]\\
&=& \sum_{a\in A}\pi(a|s)r(s, a) + \gamma\sum_{s'\in S}P(S_{t+1} = s'|S_t = s)\mathbb{E}_{\pi}[G_{t+1}|S_{t+1}=s']\\
&=& \sum_{a\in A}\pi(a|s)r(s, a) + \gamma\sum_{s'\in S}P(s'|s)V^{\pi}(s')\\
&=& \sum_{a\in A}\pi(a|s)r(s, a) + \gamma\sum_{s'\in S}\sum_{a\in A}P(S_{t+1}=s'|S_t=s, A_t=a)\pi(a|s)V^{\pi}(s')\\
&=& \sum_{a\in A}\pi(a|s)r(s, a) + \gamma\sum_{a\in A}\pi(a|s)\sum_{s'\in S} P(s'|s, a)V^{\pi}(s')\\
&=& \sum_{a\in A}\pi(a|s) \sum_{s'\in S} P(s'|s, a) r(s, a) + \gamma\sum_{a\in A}\pi(a|s)\sum_{s'\in S} P(s'|s, a)V^{\pi}(s') \\
&=& \sum_{a\in A}\pi(a|s)\sum_{s'\in S}P(s'|s, a)\left[r(s, a) + \gamma V^{\pi}(s') \right]
\end{eqnarray}$$
以上よりマルコフ決定過程からベルマン方程式が導出できることが分かります。
強化学習では、状態価値関数のほかに、行動価値関数という概念が出てきます。こちらも重要な概念で、状態価値関数と同様にベルマン方程式を導出することができます。
行動価値仮数のベルマン方程式は以下のようになります。
$$\begin{eqnarray}
Q^\pi (s, a) &=& \mathbb{E}_{\pi}[G_t|S_t=s, A_t=a]\\
&=& \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1}|S_t=s, A_t=a]\\
&=& \mathbb{E}_{\pi}[R_{t+1}|S_t=s, A_t=a] + \gamma\mathbb{E}_{\pi}[G_{t+1}|S_t=s, A_t=a]\\
&=& r(s, a) + \gamma \sum_{s'\in S} P(s'|s, a)V^\pi (s')\\
&=& r(s, a) + \gamma \sum_{s'\in S} \sum_{a'\in A} P(s'|s, a)\pi (a'|s') Q^\pi (s', a')
\end{eqnarray}$$
最後に
本記事では、強化学習を学ぶ上で最も重要な理論の1つであるマルコフ決定過程について解説してきました。
マルコフ決定過程は、奥が深く簡単なようで難しい部分があります。本記事のコンテンツをもっと追加して網羅的に紹介できる記事を目指しているので、ぜひ今後ともよろしくお願いいたします。
