Hodgkin-Huxleyモデルについて紹介していきます。
こんな方におすすめ
- 連続時間ニューロンに興味がある
- スパイキングニューラルネットワークに入門したい
などの方々にとって有益なものとなるはずです。
概要
Hodgkin-Huxleyモデルは以下の特徴があります。
Hodgkin-Huxleyモデルの特徴
- 時間の変化に伴って値が変化する連続時間ニューロン
- 4つの微分方程式により表される
- 電気回路による等価回路でモデル化
振る舞い
以下は入力と細胞膜の電位変化を可視化したものです。Hodgkin-Huxleyモデルの実装プログラムと可視化プログラムは後の方で紹介するとして、先に結果を示します。
理論
Hodgkin Huxleyモデルは以下で表される等価回路の微分方程式を解くことで求められます。
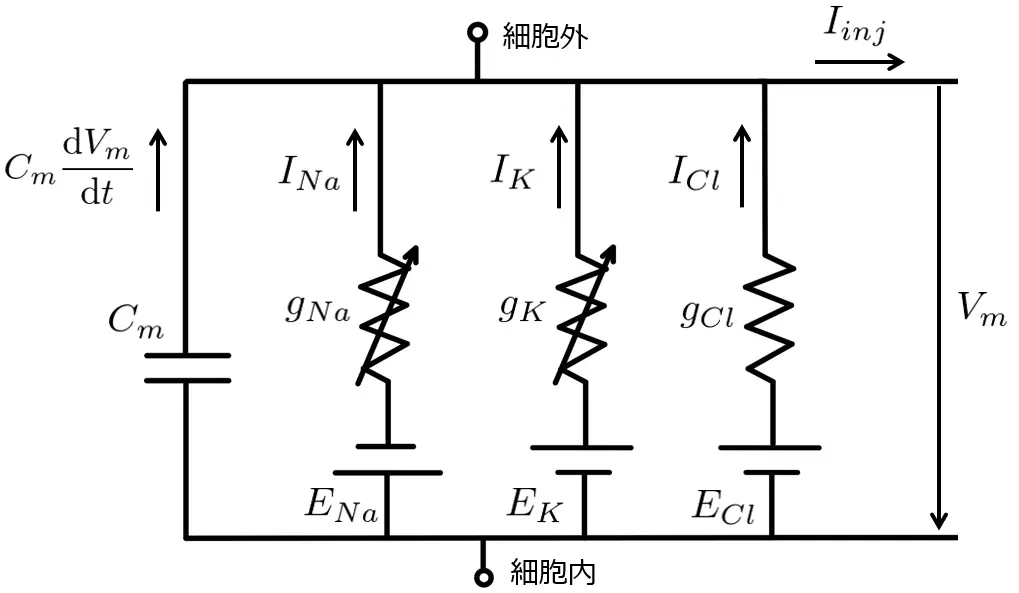
ナトリウムイオン、カリウムイオン、塩化物イオンの3つのイオンの流動で細胞膜をモデル化します。各イオンチャネルのネルンスト電位を\(E_{Na}, E_K, E_{Cl}\)、コンダクタンスを\(g_{Na}, g_K, g_{Cl}\)とする。このとき、細胞膜は上図のようなRCによる等価回路としてモデル化することができます。
このRC回路を数式で表すと以下のようになります。最終的には4つの微分方程式を解くことで膜電位の変化を求めることができます。一番上の式はキルヒホッフの第一法則(電流則)に関する等式です。
微分方程式$$
\begin{eqnarray}
\frac{\mathrm{d}V_m}{\mathrm{d}t} &=& \frac{1}{C_m}\left\{I_{inj}(t) - I_{Na}(V_m, t) - I_{K}(V_m, t) - I_{Cl}(V_m, t)\right\} \\
\frac{\mathrm{d}m(V_m, t)}{\mathrm{d}t} &=& \alpha_m(V_m) (1 - m(V_m, t)) - \beta_m(V_m) m(V_m, t) \\
\frac{\mathrm{d}h(V_m, t)}{\mathrm{d}t} &=& \alpha_h(V_m) (1 - h(V_m, t)) - \beta_h(V_m) h(V_m, t) \\
\frac{\mathrm{d}n(V_m, t)}{\mathrm{d}t} &=& \alpha_n(V_m) (1 - n(V_m, t)) - \beta_n(V_m) n(V_m, t)
\end{eqnarray}
$$
$$
\left\{
\begin{array}{lcl}
I_{Na}(V_m, t) &=& g_{Na}\cdot m(V_m, t)^3\cdot h(V_m, t)\cdot (V_m - E_{Na}) \\
I_{K}(V_m, t) &=& g_{K}\cdot n(V_m, t)^4\cdot (V_m - E_{K}) \\
I_{Cl}(V_m, t) &=& g_{Cl} \cdot (V_m - E_{Cl}) \\
\end{array}
\right.
$$
$$
\left\{
\begin{array}{lcl}
\alpha_m(V_m) &=& \frac{0.1(25- V_m)}{\exp\left\{\frac{25 - V_m}{10}\right\}-1} \\
\beta_m(V_m) &=& 4\exp\left\{-\frac{V_m}{18}\right\} \\
\alpha_h(V_m) &=& 0.07 \exp\left\{-\frac{V_m}{20}\right\} \\
\beta_h(V_m) &=& \frac{1}{\exp\left\{\frac{30 - V_m}{10}\right\} + 1} \\
\alpha_n(V_m) &=& \frac{0.01(10 - V_m)}{\exp\left\{\frac{10 - V_m}{10}\right\} - 1} \\
\beta_n(V_m) &=& 0.125 \exp\left\{-\frac{V_m}{80}\right\} \\
\end{array}
\right.
$$
Pythonによる実装
class HodgkinHuxley():
"""Full Hodgkin-Huxley Model implemented in Python"""
def __init__(self, dt=0.01, C_m=1.0, g_Na=120.0, g_K=36.0, g_L=0.3, E_Na=50.0, E_K=-77.0, E_L=-54.387):
self.dt = dt # default 0.01
self.C_m = C_m # default 1.0.
self.g_Na = g_Na # default 120.0.
self.g_K = g_K # default 36.0.
self.g_L = g_L # default 0.3.
self.E_Na = E_Na # default 50.0.
self.E_K = E_K # default -77.0.
self.E_L = E_L # default -54.387.
self.V = -65
self.m = 0.05
self.h = 0.6
self.n = 0.32
alpha_m = lambda self : 0.1 * (self.V + 40.0) / (1.0 - np.exp(-(self.V + 40.0) / 10.0))
beta_m = lambda self : 4.0 * np.exp(-(self.V + 65.0) / 18.0)
alpha_h = lambda self : 0.07 * np.exp(-(self.V + 65.0) / 20.0)
beta_h = lambda self : 1.0 / (1.0 + np.exp(-(self.V + 35.0) / 10.0))
alpha_n = lambda self : 0.01 * (self.V + 55.0) / (1.0 - np.exp(-(self.V + 55.0) / 10.0))
beta_n = lambda self : 0.125 * np.exp(-(self.V + 65) / 80.0)
I_Na = lambda self : self.g_Na * self.m**3 * self.h * (self.V - self.E_Na)
I_K = lambda self : self.g_K * self.n**4 * (self.V - self.E_K)
I_L = lambda self : self.g_L * (self.V - self.E_L)
def step(self, I_inj=0):
self.m += (self.alpha_m() * (1.0 - self.m) - self.beta_m() * self.m) * self.dt # m <- m + dm
self.h += (self.alpha_h() * (1.0 - self.h) - self.beta_h() * self.h) * self.dt # h <- h + dh
self.n += (self.alpha_n() * (1.0 - self.n) - self.beta_n() * self.n) * self.dt # n <- n + dn
self.V += ((I_inj - self.I_Na() - self.I_K() - self.I_L()) / self.C_m) * self.dt # V <- V + dV
return self.V上のクラスを定義して、インスタンス化し、細胞膜の反応を確認するための、細胞膜への入力を定義し、for文で細胞のレスポンスを収集します。
HH = HodgkinHuxley()
def generate_I_inj(t):
t = t/10
return -10*(t > 1000) + 10*(t > 2000) + 10*(t > 3000) -10*(t > 4000) \
+ 20*(t > 5000) -20*(t > 6000) + 30*(t > 7000) - 30*(t > 8000)
t = np.arange(0, 90000)
I_inj = generate_I_inj(t)
res = []
for i in I_inj:
res.append(HH.step(i))