本記事では1982年に提案されたClassicalなHopfield Networkについて詳しく知ることを目標に、解説していきたいと思います。
連想記憶とHopfield Network
連想記憶とは、ある特定の事柄から関連性のある別の事柄を思い出す能力、すなわち特定の記憶が別の記憶を引き出すという現象を指します。この連想記憶は、人間の思考パターンや知性の形成に大いに影響を及ぼしていると考えられています。

上の図は、「リンゴ」に関連する連想の具体例を示しています。私たちは「リンゴは果物」、「果物は食べ物」、「リンゴは赤い」など、多種多様な性質や側面から連想をすることができます。私たちは、物事を様々な側面から考えたり、アイディアを出したりするとき、基本的には自分の記憶をベースに連想を重ね、その連想が論理的に筋が通ているかなどを頭の中で繰り返し検証したりしています。私たちの思考や知性の構築において、このような連想的なプロセスが重要な役割を果たすことは理解いただけると思います。
それでは、この連想記憶の機能をどのように実現すれば良いのでしょうか?この問いに対する解として提案されたのが、Hopfield Network[1]という連想記憶モデルです。Hopfield Networkは、1982年にJohn Hopfieldが提唱したものです。Hopfieldが提案したこのモデルは、10年前に甘利氏が提唱したモデル[2]と全く同一であったため、時折、Amari-Hopfieldモデル[3]とも呼ばれます。
このモデルは、脳が情報を処理し、関連付け、思い出すような機能を実現することができます。そして、これらはHopfield Networkのネットワーク構造、学習方法、連想方法について理解することで、それらの機能の実現方法を知ることができます。
情報の処理 :Hopfield Networkのネットワーク構造
情報の関連付け:Hopfield Networkの学習方法
情報を思い出す:Hopfield Networkの想起方法
これらについて順に説明していきます。
Hopfield Networkの詳細
ネットワーク構造
まずは、情報処理を行うネットワーク構造について説明します。Hopfield Networkでは相互結合型のニューラルネットワークが採用されています。その理由を知るには、私たちの脳において連想記憶を司っていると考えられている海馬の構造について説明する必要があります。海馬とは大脳辺縁系を構成する部位の1つで、断面はCA1、CA2、CA3という三つの領域に区分できます。ここで特筆すべきなのは、CA3と呼ばれる部位が連想記憶と密接な関連性があると考えられている点です。CA3では、神経細胞が互いに相互接続を形成し、複雑なネットワーク構造を構築しています。この事実に基づいて、Hopfield Networkで相互結合型のネットワークを採用するというのは、生物学的な視点からも高い妥当性を持っていると言えるでしょう。
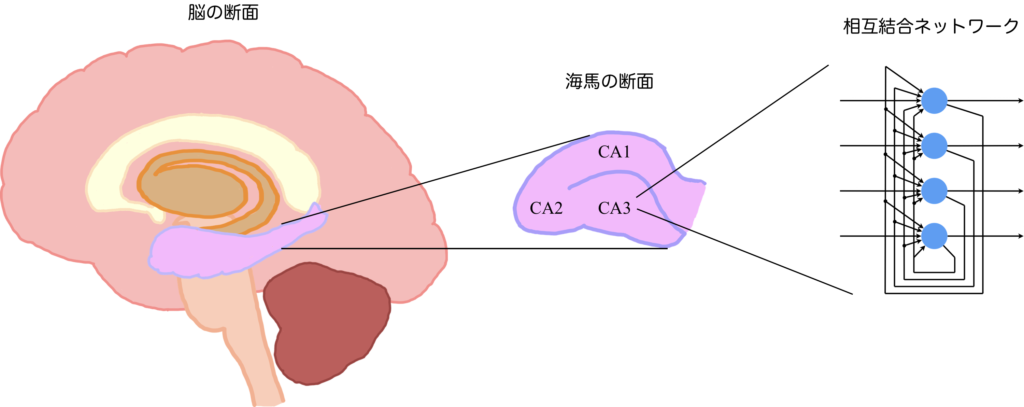
上図右に示した相互結合ネットワークは、以降の説明において不便なので、改めて相互結合ネットワークのグラフ構造について、ここで定義しておきます。上図右の相互結合ネットワークをそのままグラフに表したのが下図左です。ここで、青丸はニューロンを、黒線は結合を表しています。
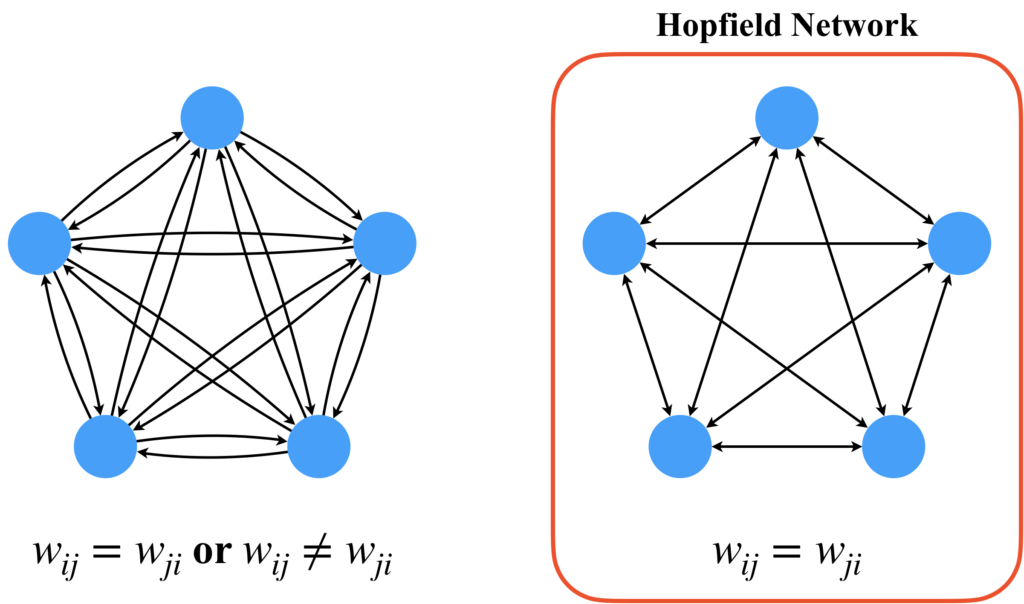
しかし、Hopfield Networkは下図左の相互結合ネットワークをそのまま使わず、幾つかの制約を加えた下図右に示すようなネットワーク構造を採用しています。詳しく説明します。あるニューロン\(i\)と\(j\)間の重みについて考えてみましょう。この重みには、\(i\rightarrow j\)の重み\(w_{ij}\)と逆方向の\(j\rightarrow i\)の重み\(w_{ji}\)の2つが考えられます。左の図ではそれぞれが別のパスとして表されており、それらの重みの間に制約はありません。しかし、Hopfield Networkでは、それらの重みの間に\(w_{ij}=w_{ji}\)という制約を設けます。一見すると、左側の図のように制約を設けずに理論を発展させた方が、より豊富な表現が可能になるかもしれませんが、右側の形式によってHopfield Networkの理論は進化してきました。これは、その特性として受け入れなければならないでしょう。理由については私は存じ上げませんが、もしかしたら計算コストや理論の構築のしやすさなどが関わってるかもしれません。
相互結合ネットワークのイラストにおいて、結合を表す線の先端の矢印は一般的に省略されます。これは、結合に方向性がないためです。また、視覚的な観点から見ても、線の端に矢印をつけずに描くことで、図全体が煩雑になることを避け、視認性を高めることが可能となります。
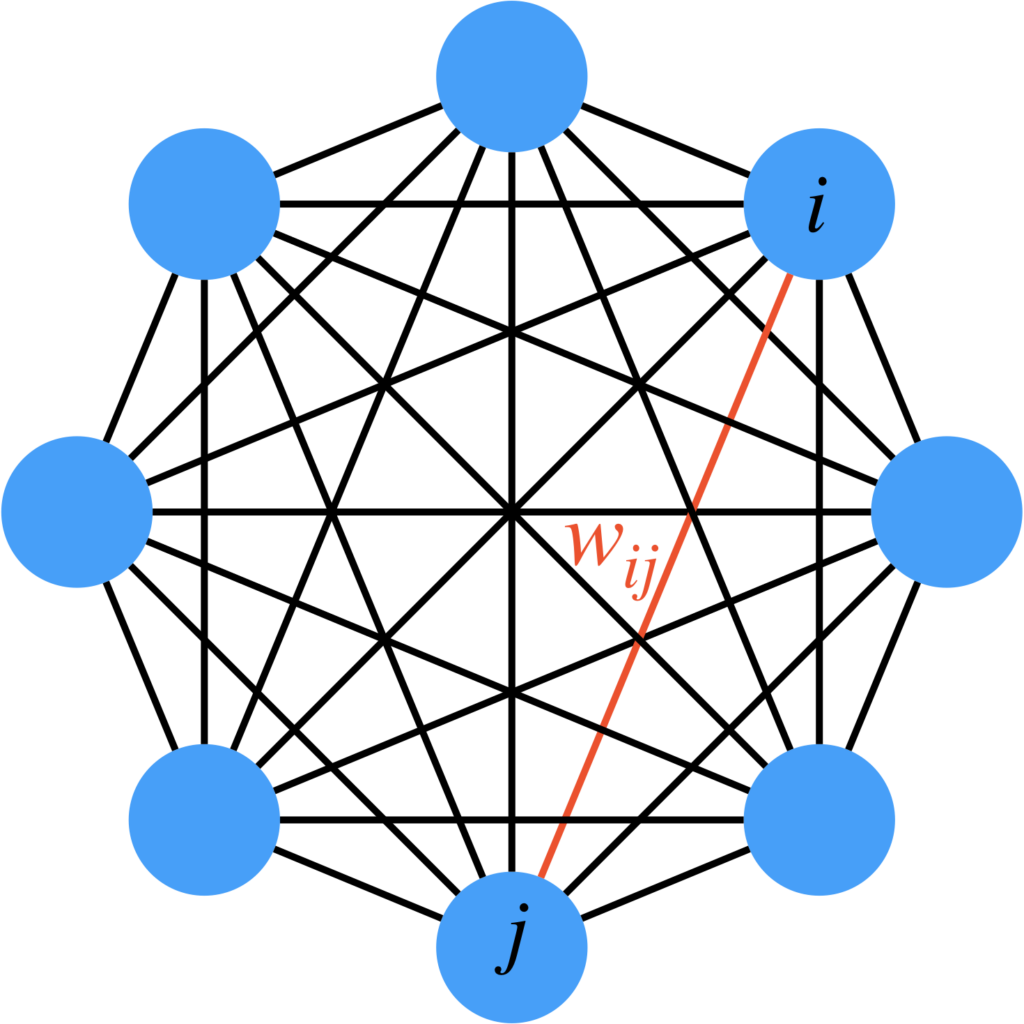
以下の図は、ニューロン数が増加したHopfield Networkのイラストです。ここでは線の両端に矢印を付けずに描いていて、矢印部分が重なって見づらくなるという事態を避けています。これ以降の説明でも、Hopfield Networkのノード間のエッジについては矢印を省略し、シンプルな線で表現します。
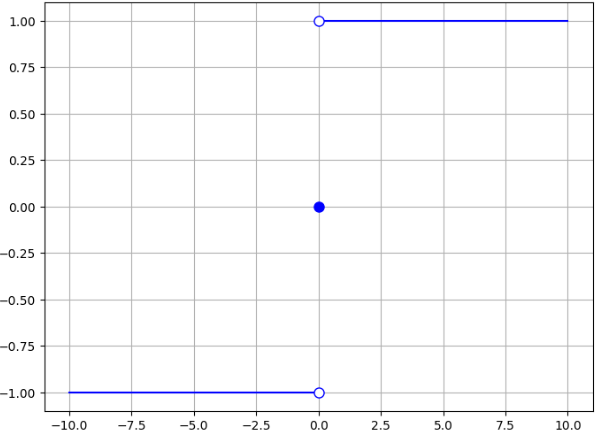
では、Hopfield Networkで用いられるニューロンのモデルについて説明します。使用されるニューロンは、状態を2つしか持たないバイナリニューロンです。活性化関数には符号関数\(\text{sgn}\)が使用されます。\(\text{sgn}\)関数は次の式で表され、グラフで表すと次のようになります。
$$
\text{sgn}(x) = \begin{cases}
1 & \text{if } x > 0\\
0 & \text{if } x = 0\\
-1 & \text{if } x < 0
\end{cases}
$$
Hopfield Networkが\(d\)個のニューロンから構成されているとします。また、\(i\)番目のニューロンと\(j\)番目のニューロンの重みを\(w_{ij}\)と表し、全てのニューロン間の重みを\(d\times d\)の行列\(\boldsymbol{W}=(w_{ij})\)として表記することにします。
※ClassicalなHopfield Networkは、自己結合を持たないモデルとして定式化されています(つまり\(w_{ii}=0\))。
ある時刻\(t\)のあるニューロン\(i\)の状態(=出力)を\(\xi_i(t)\)と書くとき、あるニューロンの次の状態は以下の式で表されます。
$$
\xi_i(t+1) = \text{sgn}\left(\sum_{j=1, j\neq i}^d w_{ij}\xi_i(t) + b_i\right)
$$
ここで、\(b\)はバイアスです。なぜ、ニューロンの応答をこのように記述することができるのかについて疑問に思いましたら、現在のニューロンモデルの祖ともいえるマカロックピッツニューロン[4]について調べてみるとよいでしょう(下図の通り)。
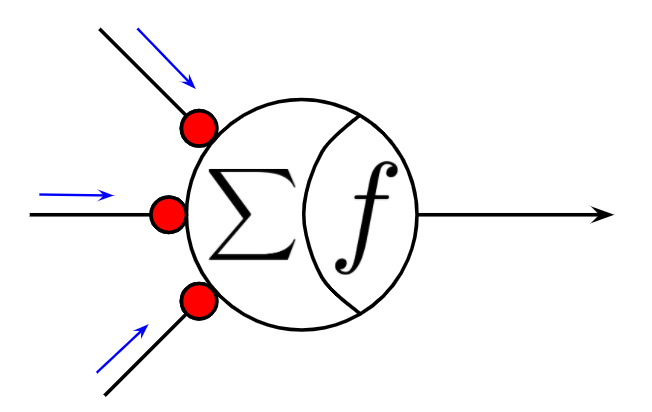
以上より、Hopfield Networkのネットワークの構造について概要が理解できたと思います。
学習方法
さて、次に情報を関連付ける仕組み、すなわち記憶する方法について説明します。
連想記憶は、ある意味でニューラルネットワークを活用したデータベースのような存在です。例えば、データベースでは一般的にSQLと呼ばれるデータベース言語が使用されます。SQLでは、新しいデータを追加するために"INSERT"文を使用します。このプロセスは、Hopfield Networkにおける"学習"に相当します。しかし、ここで言う"学習"は、深層学習における誤差逆伝播法のような複雑なプロセスではありません。
具体的には、記憶させたいデータを\(\{\boldsymbol{x}_i\}_{i=1}^N\)(\(\boldsymbol{x}_i\in\{-1, 1\}^d\))と表現したとき、Hopfield Networkの重み行列\(\boldsymbol{W} \)を以下のようにして定義するだけで記憶させることができます。
$$
\boldsymbol{W} = \sum_{i=1}^N \boldsymbol{x}_i\boldsymbol{x}_i^T
$$
たったこれだけなんです。一般的な深層学習で使用される誤差逆伝播のような複雑な最適化問題を必要とせずに学習を行うため、更に新しいデータ\(\boldsymbol{x}_{add}\)を追加で記憶させたい場合でも、追加データから計算される行列\(\boldsymbol{x}_{add}\boldsymbol{x}_{add}^T\)を既存の重み行列に加算するだけで済むのです。
$$
\boldsymbol{W} \leftarrow \boldsymbol{W} + \boldsymbol{x}_{add}\boldsymbol{x}_{add}^T
$$
※データを忘れさせたいときも、記憶済みのパターンを減算するだけで済みます。
この学習方法は、ヘブ則という原則に基づいています。ヘブ則は、同時に活動するニューロン間の接続を強化し、それ以外の接続を弱化するという原則です。行列で表現されると少々複雑に見えるかもしれませんので、特定のニューロン\(i\)と\(j\)間の重み更新式だけを見てみましょう。
$$
w_{ij} \leftarrow w_{ij} + \Delta w_{ij}\ \ (= w_{ij} + x_ix_j)
$$
この式は、\(i\)と\(j\)の両方の状態が1である場合は1を加算し、一方が1で他方が-1である場合は重みから1を減算することを意味します。このように、Hopfield Networkの学習法は非常にシンプルで直感的です。深層学習と比べて、繰り返し学習に多くの時間をかける必要がないだけでなく、新しいデータを追加する際に全てを再学習する必要がないという利点があります。この点で、Hopfield Networkは非常に効率的であり、新たな視点を提供してくれます。

想起方法
それでは、情報を思い出す方法、すなわち想起方法について説明します。まず、深層学習では、誤差逆伝播を含む様々な手法を用いて学習の最適化が行われ、推論フェーズではデータは一度だけネットワークに入力されます。これに対し、Hopfield Networkでは、データの格納は瞬時に行われます(既述の通り)が、そのデータを想起する過程は状態ベクトル\(\boldsymbol{\xi}\in\mathbb{R}^d\)(すべてのニューロンの状態をベクトルにしたもの)の各成分が変化しなくなる、つまり\(\boldsymbol{\xi}(t+1)=\boldsymbol{\xi}(t)\)となるまで繰り返されます。ここで全てのニューロンのバイアスを並べてベクトルにしたものを\(\boldsymbol{b}\in\mathbb{R}^d\)とすると、更新式は\(\boldsymbol{\xi}(t+1) = \text{sgn}(\boldsymbol{W}\boldsymbol{\xi}(t) + \boldsymbol{b})\)となります。ちなみに、この更新式は一度の計算で、全てのニューロンの状態を更新(=同期更新)しますが、実はHopfield Networkは、全てのニューロンの状態を一括で更新する同期更新ではなく、ある特定の時刻\(t\)で更新されるニューロンの数に制限を設けた非同期更新が採用されているので、更新式は厳密には異なり、一般的には、一回の更新で変化するニューロンの数は1つに限定されています(これは次に説明するエネルギー関数の想起過程における単調減少を保証するためであると考えられ、あまり大きな問題ではない)。
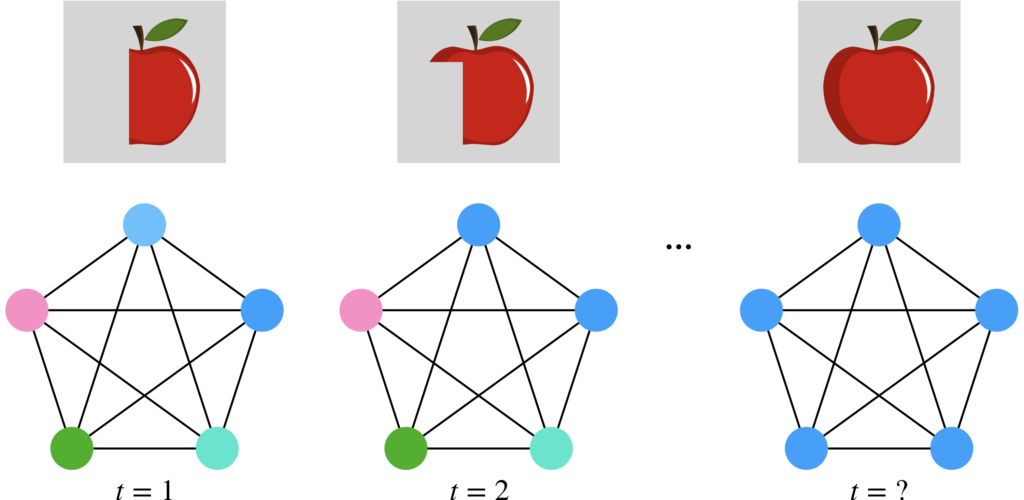
下の図を見てください。この図では、リンゴの画像を学習済みのHopfield Networkに、半分欠けたリンゴの画像を時刻\(t=1\)で入力し、その後順次ニューロンの状態を更新することで、想起する過程を視覚的に表現しています。この過程により、欠けていたリンゴの画像が徐々に明瞭になり、学習済みのリンゴの画像が浮かび上がってきます。このようにHopfield Networkを用いると、一部から全体の情報を想起することが可能になります。これは画像の想起なので私たちにとってイメージしやすいですが、単語から文章を想起する場合でも同じように考えることができます。
Hopfield Networkの特徴
ここまで示してきた内容だけで連想記憶が実現できてしまいます。複雑な最適化問題として定式化することなく、単純な仕組みで実現できるのはとても凄いことだと思います。ここでは、Hopfield Networkの特徴として、エネルギー関数と記憶容量について説明します。
エネルギー関数
実は、Hopfield Networkの想起プロセスは、あるエネルギー関数の極小値へ移動するプロセスであることが分かっています。そのエネルギー関数とは、以下のように表現されます。
$$
E = -\frac{1}{2}\boldsymbol{\xi}^T\boldsymbol{W}\boldsymbol{\xi} - \boldsymbol{\xi}^T\boldsymbol{b}
$$
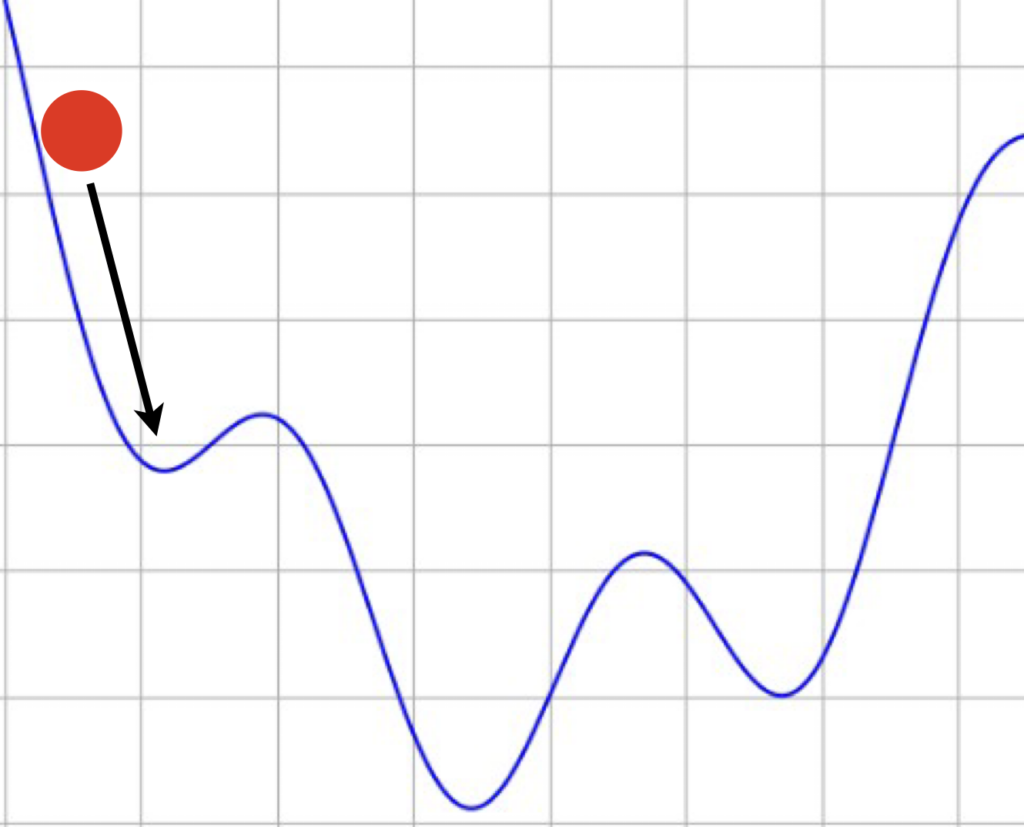
Hopfield Networkが想起するプロセスはエネルギー関数上にボールを落とし、そこからボールが勾配を沿って転がり、一番近くの局所解で停止する様子を考えると理解しやすいです。すなわち、記憶パターンはエネルギー関数の局所解となっています。
記憶容量
Hopfield Networkに記憶させるパターン数が多くなると、想起されるパターンが崩壊するなど、急激に想起できなくなる課題があります。その要因の1つにHopfield Networkの記憶容量の問題があります。本記事で説明しているClassicalなHopfield Networkの記憶容量\(C\)はおよそ\(0.138d\)とされています(ランダムなデータを記憶させる場合)。
記憶容量\(0.138d\)の効率の悪さをイメージしていただくために以下の具体例を紹介します。HDサイズ(\(1920\times1280\))の白黒画像を記憶&想起できるHopfield Networkを考えてみましょう。ニューロン数\(d\)は\(1920\times 1280=2457600\)ですので、記憶可能なパターン数は約\(339148\)となります。34万近くのHD白黒画像を記憶できるのであれば、一見凄いことに感じてしまいます。しかし、このサイズのHopfield Networkを実現することはメモリーサイズや計算資源的にかなり厳しいです。それは、\(2457600\)個のニューロンから構成されるHopfield Networkの重み行列は、\(2457600\times 2457600\)のサイズになり、1つの重み行列の各成分が4バイト(32bit)だとすると、必要なメモリー容量は\(2.4159191\times 10^{12}Byte ≒ 2416GByte\)です。たかがHD白黒画像ごときでと思えるかもしれませんが、これをHopfield Networkに保存するには想像以上のメモリーを必要とするのです。ちなみに、HD白黒画像34万枚分を画像データとして保存する場合、\(1920\times 1280\times 340000 Bit = 835584000000 Bit = 104448000000 Byte ≒ 104GByte\)のメモリが必要ですが、 Hopfield Networkにそれだけのデータを学習させるのに必要なメモリサイズ2416GByteに比べれば圧倒的に少ないです。いかに効率が悪いかをご理解いただけるのではないかと思います。
\(0.138d\)という記憶容量を改善するために、多くの研究がなされており、現在は大幅に改善しています。これについてはModern Hoppfield Networkの記事で説明します。
課題
ここでは、ClassicalなHopfield Networkの課題について説明します。先ほど、記憶容量は、0.138dであることを説明しました。しかし、これは必ずしも、その量まで必ず保存可能なことを保証するものではありません。記憶容量に全く達していなくても、想起できなくなってしまう問題があります。これは、どういうことでしょうか?
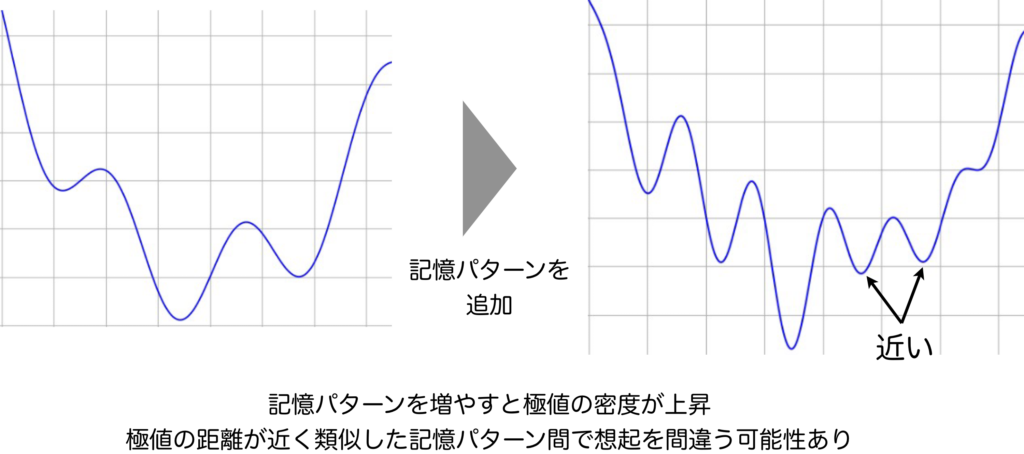
上図は、記憶パターンを増やすと、その重み行列を持つHopfield Networkのエネルギー関数に極致が増えることを表しています。記憶容量が一杯でなくても、極小値が増えればその密度は必然的に高くなり、記憶パターンによっては、とても近いところに極小値が配置されることになります。そうすると何が起こるでしょうか?
極小値が近くなると、ネットワークは混乱しやすくなり、思い通りの想起をしてくれないという状況になります。つまり、記憶パターン同士が干渉してしまっている状態です。これをクロストークと呼びます。
これを解決する方法は、多く研究されており、別の記事で扱う予定のModern Hopfield Networkでは大きく改善することができました。今回の記事では、Classical Hopfield Networkにはこのような課題が残されていたということさえ、理解していただければと思います。
参考文献
[1] Hopfield, John, "Neural Networks and Physical Systems with Emergent Collective Computational Abilities," in Proc. National Academy of Sciences, 1982.
[2] Shun-ichi Amari, "Learning patterns and pattern sequences by Self-Organizing nets of threshold elements," IEEE Transactions on Computers, 1972.
[3] H. K. Sulehria, and Ye Zhang, "Hopfield neural networks: a survey," 2007.
[4] W.S. McCulloch, and W. Pitts, "A logical calculus of the ideas immanent in nervous activity," Bulletin of Mathematical Biophysics, 1943.
